2022-2023学年苏科版数学八年级上学期期末练习卷2
试卷更新日期:2022-12-30 类型:期末考试
一、单选题(每题2分,共16分)
-
1. 下列各组数中,是勾股数的一组是( )A、2,3,4 B、3,4,5 C、0.3,0.4,0.5 D、4,5,62. 下列图形中,不是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 如图,利用尺规作图作一个角等于已知角,其依据是( )
3. 如图,利用尺规作图作一个角等于已知角,其依据是( ) A、SSS B、ASA C、SAS D、AAS4. 在平面直角坐标系中,点P(1,-)到x轴的距离为( )A、1 B、 C、 D、35. 如图,是直角三角形,点C在数轴上对应的数为 , 目 , , 若以点C为圆心,为半径画弧交数轴于点M,则A,M两点间的距离为( )
A、SSS B、ASA C、SAS D、AAS4. 在平面直角坐标系中,点P(1,-)到x轴的距离为( )A、1 B、 C、 D、35. 如图,是直角三角形,点C在数轴上对应的数为 , 目 , , 若以点C为圆心,为半径画弧交数轴于点M,则A,M两点间的距离为( ) A、0.4 B、 C、 D、6. 如图,在等边中,为中点,点 , 分别为 , 上的点, , , 在上有一动点 , 则的最小值为( )
A、0.4 B、 C、 D、6. 如图,在等边中,为中点,点 , 分别为 , 上的点, , , 在上有一动点 , 则的最小值为( ) A、7 B、8 C、9 D、107. 已知函数的图象如图所示,则函数的图象大致是( )
A、7 B、8 C、9 D、107. 已知函数的图象如图所示,则函数的图象大致是( )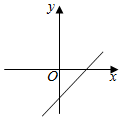 A、
A、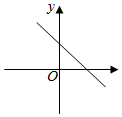 B、
B、 C、
C、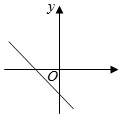 D、
D、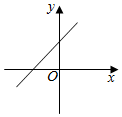 8. 如图,在∠ECF的边CE上有两点A、B,边CF上有一点D,其中BC=BD=DA且∠ECF=27°,则∠ADF的度数为( )
8. 如图,在∠ECF的边CE上有两点A、B,边CF上有一点D,其中BC=BD=DA且∠ECF=27°,则∠ADF的度数为( ) A、54° B、91° C、81° D、101°
A、54° B、91° C、81° D、101°二、填空题(每题2分,共20分)
-
9. 现定义一个新运算“※”,规定对于任意实数x,y,都有 , 则的值为 .10. 实数a,b在数轴上的位置如图所示,则化简的值是 .
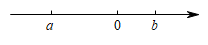 11. 比较大小:﹣3 .12. 如图,在Rt△ABC中,∠A=90°,∠B=30°,CD平分∠ACB交AB于点D,DE∥BC,交AC于点E,若BC=9,则AE的长为 .
11. 比较大小:﹣3 .12. 如图,在Rt△ABC中,∠A=90°,∠B=30°,CD平分∠ACB交AB于点D,DE∥BC,交AC于点E,若BC=9,则AE的长为 . 13. 在平面直角坐标系中,若将一次函数y=2x+m-1的图象向右平移3个单位后,得到一个正比例函数的图象,则m的值为 .14. 若函数 的图象经过点 ,其图象如图所示,则关于x的不等式 的解集为.
13. 在平面直角坐标系中,若将一次函数y=2x+m-1的图象向右平移3个单位后,得到一个正比例函数的图象,则m的值为 .14. 若函数 的图象经过点 ,其图象如图所示,则关于x的不等式 的解集为. 15. 某手工作坊生产并销售某种食品,假设销售量与产量相等,如图中的线段AB、OC分别表示每天生产成本(单位:元)、收入(单位:元)与产量x(单位:千克)之间的函数关系.若该手工作坊某一天既不盈利也不亏损,则这天的产量是千克.
15. 某手工作坊生产并销售某种食品,假设销售量与产量相等,如图中的线段AB、OC分别表示每天生产成本(单位:元)、收入(单位:元)与产量x(单位:千克)之间的函数关系.若该手工作坊某一天既不盈利也不亏损,则这天的产量是千克. 16. 如图,平分 , 于点C,且 , 已知点A到y轴的距离是4,那么点A的坐标为.
16. 如图,平分 , 于点C,且 , 已知点A到y轴的距离是4,那么点A的坐标为. 17. 若一次函数y=ax+b(a≠0)的图象经过点A(2,3),且不经过第四象限,则 4a+b的取值范围为.18. 如图,把长方形纸条依次沿着线段、折叠,且 , 得到“Z”字形图案.已知 , 要使点 , 点分别在和的延长线上(不与重合),则 .
17. 若一次函数y=ax+b(a≠0)的图象经过点A(2,3),且不经过第四象限,则 4a+b的取值范围为.18. 如图,把长方形纸条依次沿着线段、折叠,且 , 得到“Z”字形图案.已知 , 要使点 , 点分别在和的延长线上(不与重合),则 .
三、解答题(共9题,共64分)
-
19. 求下列各式中x的值:(1)、4x2﹣12=0(2)、48﹣3(x﹣2)2=020. 如图,于点E,于点F.交于点M,求证: .
 21. △ABC在平面直角坐标系中的位置如图所示,先将△ABC向右平移3个单位,再向下平移1个单位到△A1B1C1 , △A1B1C1和△A2B2C2关于x轴对称.
21. △ABC在平面直角坐标系中的位置如图所示,先将△ABC向右平移3个单位,再向下平移1个单位到△A1B1C1 , △A1B1C1和△A2B2C2关于x轴对称. (1)、画出△A1B1C1和△A2B2C2;(2)、在x轴上确定一点P , 使BP+A1P的值最小,直接写出P的坐标为;(3)、点Q在y轴上且满足△ACQ为等腰三角形,则这样的Q点有个.22. 尺规作图(保留作图痕迹,不要求写出什么作法):
(1)、画出△A1B1C1和△A2B2C2;(2)、在x轴上确定一点P , 使BP+A1P的值最小,直接写出P的坐标为;(3)、点Q在y轴上且满足△ACQ为等腰三角形,则这样的Q点有个.22. 尺规作图(保留作图痕迹,不要求写出什么作法):如图,已知 ,求作:

( 1 ) 的角平分线;
( 2 )边 上的中线.
23. 勾股定理是几何学中的明珠,它充满魅力,在现实世界中有着广泛的应用.请你尝试应用勾股定理解决下列问题:一架 长的梯子 斜靠在一竖直的墙 上,这时 为 ,如果梯子的顶端 沿墙下滑 ,那么梯子底端 向外移了多少米?(注意: ) 24. 如图,直线y=kx+4与x轴相交于点A , 与y轴相交于点B , 且AB=2 .
24. 如图,直线y=kx+4与x轴相交于点A , 与y轴相交于点B , 且AB=2 . (1)、求点A的坐标;(2)、求k的值;(3)、C为OB的中点,过点C作直线AB的垂线,垂足为D , 交x轴正半轴于点P , 试求点P的坐标及直线CP的函数表达式.25. 综合探究
(1)、求点A的坐标;(2)、求k的值;(3)、C为OB的中点,过点C作直线AB的垂线,垂足为D , 交x轴正半轴于点P , 试求点P的坐标及直线CP的函数表达式.25. 综合探究问题情境:
我们在第十一章《三角形》中学习了三角形的边与角的性质,在第十二章《全等三角形》中学习了全等三角形的性质和判定.在一些探究题中经常用以上知识转化角和边,进而解决问题.
(1)、问题初探:如图1,在△ABC中,∠ACB=90°,AC=BC,点D为直线AB上的一个动点(D与A,B不重合),连接CD,以CD为直角边作等腰直角三角形CDE,连接BE.当点D在线段AB上时,AD与BE的数量关系是;位置关系是;AB,BD,BE三条线段之间的关系是.
 (2)、类比再探:
(2)、类比再探:如图2,当点D运动到AB的延长线上时,AD与BE还存在(1)中的位置关系吗?若存在,请说明理由.同时探索AB,BD,BE三条线段之间的数量关系,并说明理由.
 (3)、能力提升:
(3)、能力提升:如图3,当点D运动到BA的延长线上时,若AB=7,AD=2,则AE=.
 26. A、B两地相距480km,甲、乙两人驾车沿同一条公路从A地出发到B地.甲、乙离开A地的路程y(km)与时间x(h)的函数关系如图所示.
26. A、B两地相距480km,甲、乙两人驾车沿同一条公路从A地出发到B地.甲、乙离开A地的路程y(km)与时间x(h)的函数关系如图所示. (1)、分别求出甲、乙离开A地的路程y(km)与时间x(h)的函数解析式及相应自变量的取值范围;(2)、甲出发多少时间后两人相距20km?27. 如图
(1)、分别求出甲、乙离开A地的路程y(km)与时间x(h)的函数解析式及相应自变量的取值范围;(2)、甲出发多少时间后两人相距20km?27. 如图 (1)、如图1,等腰直角三角形ABC中,∠ACB=90°,CB=CA,直线ED经过点C,过A作AD⊥ED于点D,过B作BE⊥ED于点E.
(1)、如图1,等腰直角三角形ABC中,∠ACB=90°,CB=CA,直线ED经过点C,过A作AD⊥ED于点D,过B作BE⊥ED于点E.求证:△BEC≌△CDA;
(2)、【模型应用】①已知直线l1:y= x+4与坐标轴交于点A、B,将直线l1绕点A逆时针旋转45o至直线l2 , 如图2,求直线l2的函数表达式;②如图3,长方形ABCO,O为坐标原点,点B的坐标为(8,-6),点A、C分别在坐标轴上,点P是线段BC上的动点,点D是直线y=-2x+6上的动点且在第四象限.若△APD是以点D为直角顶点的等腰直角三角形,请直接写出点D的坐标.