山东省济宁市邹城市2022-2023学年高三上学期数学期中考试试卷

试卷更新日期：2022-12-30 类型：期中考试

进入出卷网下载

一、单选题

1. 已知集合 $A = {x | | x | < 3 ， x \in Z}$ ， $B = {x ∣ x < - \frac{3}{2}$ 或 $x > 4}$ ，则 $A \cap (∁_{R} B) =$ （）

A、 ${- 1 ， 0 ， 1 ， 2}$ B、 ${- 2 ， - 1 ， 0 ， 1 ， 2}$ C、 ${x ∣ - \frac{3}{2} \leq x < 3}$ D、 ${x ∣ - 3 < x < - \frac{3}{2}}$

查看试题解析
2. 已知复数 $z = (a + 2 i) (- i) (a \in R)$ 的实部与虚部的和为3，则 $\bar{z} =$ （）

A、 $2 + i$ B、 $2 - i$ C、 $1 + 2 i$ D、 $- 1 - 2 i$

查看试题解析
3. 已知 $\vec{a} ， \vec{b}$ 都是单位向量，其夹角为 $\frac{3 π}{4}$ ，若向量 $\vec{m} = \vec{a} - \sqrt{2} \vec{b}$ ，则 $| \vec{m} | =$ （）

A、5 B、2 C、 $\sqrt{5}$ D、 $\sqrt{2}$

查看试题解析
4. 要得到函数 $y = c o s (2 x - \frac{π}{6})$ 的图像，只需将函数 $y = s i n 2 x$ 的图像

A、向右平移 $\frac{π}{3}$ 个单位长度 B、向左平移 $\frac{π}{3}$ 个单位长度 C、向右平移 $\frac{π}{6}$ 个单位长度 D、向左平移 $\frac{π}{6}$ 个单位长度

查看试题解析
5. 在长方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 中，直线 $A_{1} C$ 与平面 $A B_{1} D_{1}$ 的交点为 $M$ ，与平面 $B D C_{1}$ 的交点为 $N ， O$ 为线段 $B_{1} D_{1}$ 的中点，则下列结论错误的是（）

A、 $A ， O ， M$ 三点共线 B、 $N ， O ， A_{1} ， A$ 四点共面 C、 $M ， N$ 为线段 $A_{1} C$ 的四等分点 D、线段 $M N$ 的中点在平面 $B B_{1} D_{1} D$ 上

查看试题解析
6. 设等差数列 ${a_{n}}$ 的前 $n$ 项的和为 $S_{n} ， a_{5} = 9 ， a_{2} + a_{7} = 16$ ，则下列结论不正确的是（）

A、 $a_{n} = 2 n - 1$ B、 $a_{3} + a_{6} = 16$ C、 $S_{n} = n^{2} + n$ D、数列 ${\frac{1}{a_{n} a_{n + 1}}}$ 的前 $n$ 和为 $\frac{n}{2 n + 1}$

查看试题解析
7. 已知函数 $f (x) = l o g_{2} x + 2^{x}$ ，若 $f (3 x - 2) < 5$ ，则实数 $x$ 的取值范围（）

A、 $(\frac{2}{3} ， \frac{7}{3})$ B、 $(\frac{2}{3} ， \frac{4}{3})$ C、 $(- \infty ， \frac{7}{3})$ D、 $(- \infty ， \frac{4}{3})$

查看试题解析
8. 设半径为 $R$ 的球面上有 $A ， B ， C ， D$ 四点，且 $A B ， A C ， A D$ 两两垂直，若 $S_{△ A B C} + S_{△ A C D} + S_{△ A B D} = 8$ ，则球半径 $R$ 的最小值是（）

A、2 B、 $\sqrt{2}$ C、 $2 \sqrt{2}$ D、4

查看试题解析

二、多选题

9. 若 $a > b > 0 ， c \neq 0$ ，则下列不等式中恒成立的是（）

A、 $\frac{1}{a} > \frac{1}{b}$ B、 $l g a > l g b$ C、 $a c > b c$ D、 $202 2^{a - b} > 1$

查看试题解析
10. 已知函数 $f (x) = x^{3} - 3 x + 1$ ，则（）

A、函数 $f (x)$ 有两个极值点 B、函数 $f (x)$ 有三个零点 C、若 $g (x) = f^{'} (x)$ ，则 $g (x)$ 是偶函数 D、点 $(1 ， 1)$ 是函数 $y = f (x + 1)$ 的对称中心

查看试题解析
11. 已知函数 $f (x) = A s i n (ω x + \frac{π}{4}) (ω > 0 ， A > 0)$ ，若 $x = \frac{3 π}{2}$ 为 $f (x)$ 的一个极值点，且 $f (x)$ 的最小正周期为 $T$ ，若 $π < T < 2 π$ ，则（）

A、 $ω = \frac{3}{2}$ B、 $A = f (\frac{3 π}{2})$ C、 $f (x + \frac{π}{3})$ 为偶函数 D、 $f (x)$ 的图象关于点 $(\frac{7 π}{6} ， 0)$ 对称

查看试题解析
12. 已知函数 $f (x)$ 的定义域为 $R$ ，满足 $f (x + 3) + f (x + 1) = 0$ ，且 $f (x + 1)$ 为偶函数，则（）

A、 $f (2) = 0$ B、 $f (x)$ 为偶函数 C、 $f (x)$ 为周期函数 D、 $f (x + 4)$ 为偶函数

查看试题解析

三、填空题

13. 已知函数 $f (x) = e^{x} + x^{2} - a x$ 在点 $(1 ， f (1))$ 处切线的斜率是3，则实数 $a =$ .

查看试题解析
14. 在 $△ A B C$ 中，若 $a^{2} + b^{2} - \frac{1}{2} a b = c^{2} ， a b = 4$ ，则 $△ A B C$ 的面积是.

查看试题解析
15. 若 $3 s i n α + s i n β = \sqrt{10}$ ，且 $α + β = \frac{3 π}{2}$ ，则 $s i n α =$ .

查看试题解析
16. 已知函数 $g (x) = a e^{x} - l n x + l n a$ ，若在其定义域内总有 $g (x) \geq 0$ 成立，则实数 $a$ 的取值范围为.

查看试题解析

四、解答题

17. 已知不等式 $\frac{2 x - 1}{x - 2} \geq 1$ 的解集是集合 $A$ ，函数 $f (x) = l g [x^{2} - (2 a + 1) x + a^{2} + a]$ 的定义域是集合 $B$ .

(1)、分別求集合 $A ， B$ ；

(2)、若 $x ∈ B$ 是 $x ∈ A$ 成立的必要不充分条件，试求实数 $a$ 的取值范围.

查看试题解析
18. 现有一张半径为2米的圆形铁皮，从中裁剪出一块扇形铁皮（如图1中阴影部分），并卷成一个深度为h米的圆锥筒（如图2的）容器.

(1)、若所裁剪的扇形铁皮的弧长为 $2 π$ 米，求圆锥简容器的容积；

(2)、当圆锥简容器的深度h为多少米时，其容积最大？并求其容积的最大值.

查看试题解析
19. 如图，已知 $\vec{O M} = \vec{a} ， \vec{O N} = \vec{b}$ ，平面内任意点 $A$ 关于点 $M$ 的对称点为 $B$ ，点 $B$ 关于点 $N$ 的对称点为 $C$ .设 $\vec{a} - \vec{b} = \vec{e}$ （ $\vec{e}$ 为单位向量）.

(1)、求 $A C$ 的长；

(2)、在 $△ A B C$ 中，若 $A B s i n 2 B = A C s i n C$ ，试求 $A B + B C$ 的取值范围.

查看试题解析
20. 已知数列 ${a_{n}} ， a_{1} = 2$ ，且满足 $n \in N^{*}$ ，有 $a_{n} \cdot a_{n + 1} = 2^{2 n + 1}$ .

(1)、求数列 ${a_{n}}$ 的通项公式 $a_{n}$ ：

(2)、若 $b_{n} = a_{n} (a_{n} - 1)$ ，设数列 ${b_{n}}$ 的前 $n$ 项和为 $S_{n}$ ，试求和： $\frac{2}{S_{1}} + \frac{2^{2}}{S_{2}} + \frac{2^{3}}{S_{3}} + ⋯ + \frac{2^{n}}{S_{n}}$ .

查看试题解析
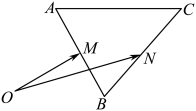21. 2022中国国际智能产业博览会于8月22~24日在重庆隆重举办，主题延续“智能化：为经济赋能，为生活添彩”，某企业遵循国家发展战略目标，进一步优化内部结构，深入拓展大数据智能化建设，据悉，该企业研发部原有80人，年人均投入a（ $a > 0$ ）万元，现把研发部人员分成两类：技术人员和研发人员，其中技术人员有x名（ $x \in N^{*}$ 且 $45 \leq x \leq 75$ ），调整后，研发人员的年人均投入增加 $4 x %$ ，技术人员的年人均投入为 $a (m - \frac{2 x}{25})$ （其中 $m \in R$ 且 $m > 0$ ）万元.

(1)、要使调整后的研发人员的年总投入不低于调整前的80人的年总投入，则优化结构调整后的技术人员x的取值范围是多少？

(2)、若研发部新招聘1名员工，原来的研发部人员调整策略不变，且同时满足下列两个条件：①技术人员的年人均投入始终不减少；②调整后研发人员的年总投入始终不低于调整后技术人员的年总投入.请分析是否存在满足上述条件的正实数m，若存在，则求出m的值；若不存在，则说明理由.

查看试题解析
22. 已知函数 $f (x) = l n x ， f^{'} (x)$ 是函数 $f (x)$ 的导函数.

(1)、求函数 $g (x) = f (x) + a f^{'} (x) (a \in R)$ 的单调区问；

(2)、设 $b > a > 0$ ，试比较 $\frac{b + a}{2}$ 与 $\frac{b - a}{f (b) - f (a)}$ 的大小，并说明理由；

(3)、若数列 ${a_{n}}$ 的通项 $a_{n} = 1 + \frac{1}{2} + \frac{1}{3} + ⋯ + \frac{1}{n}$ ，求证： $l n (2 n + 1) > a_{n}$ .

查看试题解析