四川省泸州市泸县2022-2023学年九年级上学期12月第一次教学质量诊断性模拟考试数学试题

试卷更新日期：2022-12-30 类型：月考试卷

进入出卷网下载

一、选择题：本大题共12小题，每小题3分，共36分．

1. 一元二次方程 $4 x^{2} - 2 x + \frac{1}{4} = 0$ 根的情况是（　　）

A、没有实数根 B、只有一个实数根 C、有两个相等的实数根 D、有两个不相等的实数根

查看试题解析
2. 2020年2月11日，世卫组织在日内瓦召开发布会，宣布将新型冠状病毒肺炎正式命名为“ $COVID-19$ ”；“ $COVID$ ”中将每一个字母看成一个图形，那么是中心对称图形的个数为（）

A、0 B、1 C、2 D、3

查看试题解析
3. 已知 $x = 1$ 是关于x的一元二次方程 $x^{2} + m x = 0$ 的一个根，则m的值是（）

A、-1 B、0 C、1 D、2

查看试题解析
4. 点 $P (2 ， - 5)$ 关于原点的对称点的坐标是（）

A、 $(- 2 ， - 5)$ B、 $(2 ， 5)$ C、 $(- 2 ， 5)$ D、 $(- 5，2)$

查看试题解析
5. 一元二次方程 $x^{2} - 6 x - 11 = 0$ 配方后是（）

A、 ${(x - 3)}^{2} = 2$ B、 ${(x - 3)}^{2} = 20$ C、 ${(x + 3)}^{2} = 2$ D、 ${(x + 3)}^{2} = 20$

查看试题解析
6. 下列所给的事件中，是必然事件的是（）

A、某校的300名学生中，至少有2名学生的生日是同一天 B、正方形的对角线互相垂直 C、某抽奖活动的中奖概率是 $\frac{1}{10}$ ，那么连续抽10次，必然会中奖 D、2023年的元旦顺德会下雪

查看试题解析
7. 肆虐的冠状病毒肺炎具有人传人性，调查发现：1人感染病毒后如果不隔离，那么经过两轮传染将累计会有225人感染，若设1人平均感染 $x$ 人，依题意可列方程

A、 $1 + x = 225$ B、 $1 + x^{2} = 225$ C、 $1 + x + x^{2} = 225$ D、 ${(1 + x)}^{2} = 225$

查看试题解析
8. 如图， $△ A B C$ 和 $△ D E F$ 是以点 $O$ 为位似中心的位似图形，若 $O A ： A D = 2 ： 3$ ，则 $△ A B C$ 与 $△ D E F$ 的周长比是（）

A、2：3 B、3：2 C、2：5 D、5：2

查看试题解析
9. 如图，在 $⊙ O$ 中， $A B = A C$ ，若 $∠ A B C = 65 °$ ，则 $∠ B O C$ 的度数为（）

A、 $130 °$ B、 $100 °$ C、 $120 °$ D、 $110 °$

查看试题解析
10. 二次函数 $y = x^{2} - 2 x - 3$ ．若 $y > - 3$ ，则自变量x的取值范围是（）

A、 $x < 0$ 或 $x > 2$ B、 $x < 1$ 或 $x > 3$ C、 $0 < x < 2$ D、 $1 < x < 3$

查看试题解析
11. 如图，半圆O的直径 $A B = 20$ ，弦 $A C = 12$ ，弦 $A D$ 平分 $∠ B A C$ ， $A D$ 的长为（）

A、 $4 \sqrt{5}$ B、 $6 \sqrt{5}$ C、 $8 \sqrt{5}$ D、 $10 \sqrt{5}$

查看试题解析
12. 如图是二次函数 $y = a x^{2} + b x + c$ 图象的一部分，图象过点 $A (- 3 ， 0)$ ，对称轴为直线 $x = - 1$ ， ① $b^{2} - 4 a c > 0$ ② $4 a + c < 0$ ③当 $- 3 \leq x \leq 1$ 时， $y \geq 0$ ④若 $B (- \frac{5}{2} ， y_{1})$ ， $C (- \frac{1}{2} ， y_{2})$ 为函数图象上的两点，则 $y_{1} > y_{2}$ ，以上结论中正确的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题(3分每题，共12分)

13. 二次函数 $y = x^{2} - 2 x + m$ 的图象与 $x$ 轴只有一个公共点，则 $m$ 的值为．

查看试题解析
14. 若 $a$ ， $b$ 是方程 $2 x^{2} + 4 x - 3 = 0$ 的两根，则 $a^{2} + a b - 2 b =$ .

查看试题解析
15. 如图， $A B$ 是 $⊙ O$ 的弦，C是 $A B$ 的中点， $O C$ 交 $\overset{⏜}{A B}$ 于点D．若 $A B = 8$ cm， $C D = 2$ cm，则 $⊙ O$ 的半径为 cm．

查看试题解析
16. 如图，在平面直角坐标系中，点A在y轴的正半轴上， $O A = 1$ ，将 $O A$ 绕点O顺时针旋转 $45^{°}$ 到 $O A_{1}$ ，扫过的面积记为 $S_{1}$ ， $A_{1} A_{2} ⊥ O A_{1}$ 交x轴于点 $A_{2}$ ；将 $O A_{2}$ 绕点O顺时针旋转 $45^{°}$ 到 $O A_{3}$ ，扫过的面积记为 $S_{2}$ ， $A_{3} A_{4} ⊥ O A_{3}$ 交y轴于点 $A_{4}$ ；将 $O A_{4}$ 绕点O顺时针旋转 $45^{°}$ 到 $O A_{5}$ ，扫过的面积记为 $S_{3}$ ， $A_{5} A_{6} ⊥ O A_{5}$ 交x轴于点 $A_{6}$ ；…；按此规律，则 $S_{2022}$ 的值为．

查看试题解析

三、解答题(每小题6分，共18分)

17. 解方程： $2 {(x + 3)}^{2} = x (x + 3)$ ．

查看试题解析
18. 已知二次函数的图象顶点为 $P (- 2 ， 2)$ ．且过点为 $A (0 ， - 2)$ ，求该抛物线的解析式．

查看试题解析
19. 如图， $∠ C A B = ∠ C B D$ ， $A B = 4$ ， $A C = 6$ ， $B D = 7.5$ ， $B C = 5$ ，求 $C D$ 的长．

查看试题解析

四、解答题(每小题7分，共14分)

20. 如图方格纸中每个小正方形的边长都是1个单位长度，在方格纸中建立如图所示的平面直角坐标系， $Δ A B C$ 的顶点都在格点上，且三个顶点的坐标分别为 $A (0 ， 3)$ ， $B (3 ， 4)$ ， $C (2 ， 2)$ ．

⑴画出 $△ A B C$ 关于原点O的中心对称图形 $△ A^{'} B^{'} C^{'}$ ，并写出点B的对应点 $B^{'}$ 的坐标．

⑵画出将 $△ A B C$ 绕原点O逆时针方向旋转90度后的图形 $△ A^{''} B^{''} C^{''}$ ．

查看试题解析
21. 某商场以每件20元的价格购进一种商品，经市场调查发现：该商品每天的销售量 $y$ （件）与每件售价 $x$ （元）之间满足一次函数关系，其图象如图所示.设该商场销售这种商品每天获利 $w$ （元）.

(1)、求 $y$ 与之间的函数关系式；

(2)、求 $w$ 与 $x$ 之间的函数关系式；

(3)、该商场规定这种商品每件售价不低于进价且不高于38元，商品要想获得600元的利润，每件商品的售价应定为多少元？

查看试题解析

五、解答题(每小题8分，共16分)

22. 为了解市区A校落实双减政策的情况，有关部门抽查了A校901班同学，以该班同学参加课外活动的情况为样本，对参加“球类”、“绘画类”、“舞蹈类”、“音乐类”、“棋类”活动的情况进行调查统计，并绘制了如图所示的统计图.

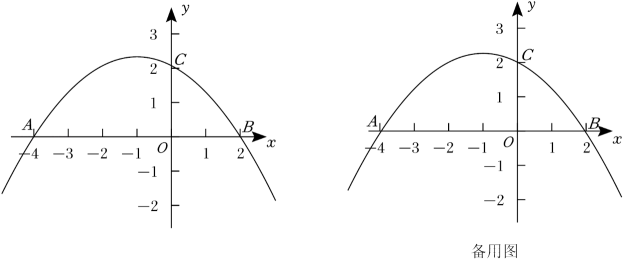
(1)、该班参加球类活动的学生占班级人数的百分比是；

(2)、请把图2（条形统计图）补充完整：

(3)、该校学生共720人，则参加棋类活动的人数约为.

(4)、该班参加舞蹈类活动的4位同学中，恰有2位男生（分别用 $E ， F$ 表示）和2位女生（分别用 $G ， H$ 表示），现准备从中选取两名同学组成舞伴，请用列表或画树状图的方法求恰好选中一男一女的概率.

查看试题解析
23. 抛物线 $y ＝ x^{2} + b x + c$ 经过点 $A (- 1 ， 0)$ ，点 $B (2 ， - 3)$ ，与y轴交于点C，抛物线的顶点为D．

(1)、求抛物线的解析式；

(2)、当 $0 < x < 4$ 时，y的取值范围是；

(3)、抛物线上是否存在点P，使 $△ PBC$ 的面积是 $△ B C D$ 面积的4倍，若存在，点P的坐标；若不存在，请说明理由．

查看试题解析

六、解答题(24小题12分，25小题12分，共24分)

24. 在Rt△ABC中，∠ACB＝90°，以AC为直径的⊙O交AB于点D，点E是边BC的中点，连结DE.

(1)、求证：DE是⊙O的切线；

(2)、若AD＝4，BD＝9，求⊙O的半径.

查看试题解析
25. 如图，抛物线y＝ax²+bx+c与x轴交于A（﹣4，0），B（2，0），与y轴交于点C（0，2）.

(1)、求这条抛物线所对应的函数的表达式；

(2)、若点D为该抛物线上的一个动点，且在直线AC上方，求点D到直线AC的距离的最大值及此时点D的坐标；

(3)、点P为抛物线上一点，连接CP，直线CP把四边形CBPA的面积分为1：5两部分，求点P的坐标.

查看试题解析