浙江省杭州市余杭区、临平区、富阳区等多区2022-2023学年九年级上学期12月月考数学试题

试卷更新日期：2022-12-30 类型：月考试卷

进入出卷网下载

一、选择题：本大题有10个小题，每小题3分，共30分．

1. 若2x＝5y，则 $\frac{x}{y}$ 的值是（）

A、 $\frac{2}{5}$ B、 $\frac{5}{2}$ C、 $\frac{4}{5}$ D、 $\frac{5}{4}$

查看试题解析
2. 将函数y＝－(x＋4)²＋1的图象向右平移4个单位所得新的函数图象的对称轴是（）

A、y轴 B、直线x＝8 C、直线x＝－4 D、直线x＝4

查看试题解析
3. 下列一定相似的两个图形是（）

A、有一个角是45°的等腰三角形 B、有一个角是60°的三角形 C、等腰三角形 D、有一个角是120°的等腰三角形

查看试题解析
4. 如图，已知AB∥CD∥EF，那么下列结论中正确的是（）

A、 $\frac{A D}{D F} = \frac{B C}{C E}$ B、 $\frac{B C}{C E} = \frac{D F}{A D}$ C、 $\frac{C D}{E F} = \frac{B C}{B E}$ D、 $\frac{C D}{E F} = \frac{A D}{A F}$

查看试题解析
5. 一个不透明的布袋里装有4个白球，2个红球，1个黄球，它们只有颜色不同．从布袋里任意摸出一个球是红球的概率为（）

A、 $\frac{4}{7}$ B、 $\frac{3}{7}$ C、 $\frac{2}{7}$ D、 $\frac{1}{7}$

查看试题解析
6. 已知⊙O的半径为6，点P在⊙O内，则线段OP长（）

A、小于6 B、大于6 C、等于6 D、等于12

查看试题解析
7. 如图，下列条件不能判定△ADB∽△ABC的是（）

A、∠ABD＝∠ACB B、∠ADB＝∠ABC C、 $A B^{2} = A D \cdot A C$ D、 $\frac{A D}{A B} = \frac{A B}{B C}$

查看试题解析
8. 已知二次函数 $y = a {(x - m)}^{2} (a > 0)$ 的图象经过点 $A (- 1 ， p)$ ， $B (3 ， q)$ ，且 $p < q$ ，则 $m$ 的值不可能是（）

A、-2 B、 $- \sqrt{2}$ C、0 D、 $\frac{5}{2}$

查看试题解析
9. 如图，已知圆的内接四边形ABDC，边DC与BA的延长线交于点Q，对角线AD与CB交于点P．有下列结论：①△CPD∽△APB；②△APC∽△BPD；③△DCA∽△BAC；④△QCA∽△QBD，其中正确的是（）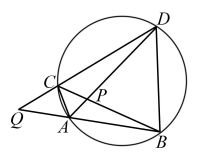

A、②③④ B、①③ C、①②④ D、②③

查看试题解析
10. 已知，二次函数 $y = a x^{2} + b x + c (a ， b ， c$ 是常数，且 $a \neq 0)$ 图象的对称轴为直线 $x = 1$ ，点 $A (x_{1} ， y_{1}) ， B (x_{2} ， y_{2}) (y_{1} < y_{2})$ 在该函数的图象上.（）

A、若 $x_{1} < x_{2}$ ，则 $x_{1} + x_{2} - 2 < 0$ B、若 $x_{1} < x_{2}$ ，则 $x_{1} + x_{2} - 2 > 0$ C、若 $x_{1} > x_{2}$ ，则 $a (x_{1} + x_{2} - 2) > 0$ D、若 $x_{1} > x_{2}$ ，则 $a (x_{1} + x_{2} - 2) < 0$

查看试题解析

二、填空题：本题有6个小题，每小题4分，共24分．

11. 四边形ABCD内接于⨀O．若∠A＝50°，则∠BCD＝°．

查看试题解析
12. 已知点P是线段AB的黄金分割点，AP＞PB．若AB＝2，则AP＝．

查看试题解析
13. 如图，在⊙O中，OC⊥AB于点C．若⊙O的半径为10，AB＝16，则OC＝．

查看试题解析
14. 在平面直角坐标系xOy中，将二次函数y＝ax²－4ax＋c(a为常数，且a＜0)的图象沿着y轴向下平移，交x轴于O，A两点，则OA的长为．

查看试题解析
15. 如图，在△ABC中，点D，E分别在边AB，AC上，AD∶DB＝3∶2，AE∶EC＝1∶2，直线ED和CB的延长线交于点F，则 $\frac{F B}{F C} =$ ．

查看试题解析
16. 若实数a，b满足a＋b²＝2，则a满足的范围是， a²＋5b²的最小值为．

查看试题解析

三、解答题：本题有7小题，共66分．

17. 已知 $\frac{a}{b} = \frac{c}{d}$ .
判断 $\frac{a - b}{a} = \frac{c - d}{c}$ 是否成立，并说明理由.

查看试题解析
18. 有4张正面分别写着数字－1，1，2，3的不透明卡片，它们除数字外完全相同，将它们背面朝上洗均匀．

(1)、随机抽取一张，记下数字后放回洗均匀，再随机抽取一张记下数字，前后两次抽取的数字分别记为m，n．用列表或画树状图法求点P(m，n)在第二象限的概率．

(2)、随机抽取一张记下数字(不放回)，再从余下的3张中随机抽取一张记下数字，前后两次抽取的数字分别记为m，n，求点P(m，n)在第二象限的概率．

查看试题解析
19. 如图，四边形ABCD，DCFE，EFGH是三个边长为1的正方形，连结AC，AF，AG．

(1)、求证：△ACF∽△GCA．

(2)、求∠1＋∠2＋∠3的度数．

查看试题解析
20. 如图，在△ABC中，AB＝AC，以AB为直径的半圆O分别交BC，AC于点D，E，连接DE，OD．

(1)、求证： $\overset{⌢}{B D} = \overset{⌢}{E D}$ ．

(2)、当 $\overset{⌢}{A E}$ ， $\overset{⌢}{B E}$ 的度数之比为4∶5时，求四边形ABDE四个内角的度数．

查看试题解析
21. 已知，在平面直角坐标系内，二次函数y＝-x²+px+q的图象与一次函数y＝mx+n的图象交于点B(3，0)，C(0，－3)．

(1)、求二次函数图象顶点坐标；

(2)、若-x²+px+q＞mx+n，结合函数图象回答x的取值范围．

查看试题解析
22. 如图，△ABC内接于⊙O，AE为直径，AD⊥BC于点D，EF⊥BC于点F．

(1)、求证：∠DAC＝∠BAE；

(2)、当点C是 $\overset{⌢}{A E}$ 的中点时，求证：FC＝AD．

查看试题解析
23. 在平面直角坐标系xOy中，二次函数y＝ax²＋bx＋c的图象经过点A(0，－4)和B(2，0)．

(1)、①求a，b之间的等量关系式．
②若0＜x₁＜x₂＜2时，总有y₁＜y₂ ，求a的取值范围．

(2)、函数y₁的图象经过两个不同的点M(p，m)，N(－2－p，n)．①若m＝n，求a的值；②若m＝－2p－3，n＝2p＋1，请说明点M和点N都在函数y₂＝－2x－3的图象上，并求出a的值．

查看试题解析