四川省达州市通川区蒲家中学2022-2023学年九年级上学期数学第三次月考测试题

试卷更新日期：2022-12-30 类型：月考试卷

进入出卷网下载

一、单项选择题（共30分）

1. 下列计算正确的是（）

A、2x+3y＝5xy B、（2x²）³＝3x⁶ C、x⁶÷x²＝x⁴ D、（x+y）²＝x²+y²

查看试题解析
2. 如图所示的立体图形，它的主视图是（）

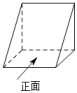A、 B、 C、 D、

查看试题解析
3. 如图，一个梯子靠在垂直水平地面的墙上，梯子AB的长是2米．若梯子与地面的夹角为 $α$ ，则梯子顶端到地面的距离（BC的长）为（）

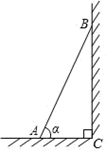A、 $2 \sin α$ 米 B、 $2 \cos α$ 米 C、 $\frac{2}{\sin α}$ 米 D、 $\frac{2}{\cos α}$ 米

查看试题解析
4. 下列命题是真命题的是（）

A、对边相等的四边形是平行四边形 B、有一个角是90°的平行四边形是矩形 C、邻边相等的四边形是菱形 D、对角线互相垂直的平行四边形为正方形

查看试题解析
5. 如图是交警在一个路口统计的某个时段来往车辆的车速（单位：千米/时）情况．则这些车的车速的众数、中位数分别是（）

A、8，6 B、8，5 C、52，53 D、52，52

查看试题解析
6. 在以下三个图形中，根据尺规作图的痕迹，能判断射线AD平分∠BAC的是（）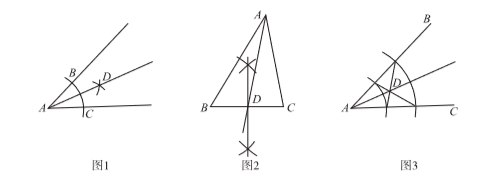

A、图2 B、图1与图2 C、图1与图3 D、图2与图3

查看试题解析
7. 在△ABC中， $(\sqrt{3} t a n A - 3)^{2} + | 2 c o s B - \sqrt{3} | = 0$ ，则△ABC为（）

A、等腰直角三角形 B、有60°角的直角三角形 C、等边三角形 D、顶角为120°的等腰三角形

查看试题解析
8. 已知点（﹣2，a），（2，b），（3，c）在函数y＝ $\frac{k}{x}$ （k＞0）的图象上，则下列判断正确的是（　　）

A、a＜b＜c B、b＜a＜c C、a＜c＜b D、c＜b＜a

查看试题解析
9. 如图，菱形ABCD中，∠BAD＝60°，AC、BD交于点O，E为CD延长线上的一点，且CD＝DE，连接BE分别交AC，AD于点F、G，连接OG、AE.则下列结论：①OG＝ $\frac{1}{2}$ AB； ②四边形ABDE是菱形；③S_四边形_ODGF＝S_△_ABF；其中正确的是（）

A、①② B、①③ C、②③ D、①②③

查看试题解析
10. 如图，矩形ABCD的顶点A、C分别在x、y轴的正半轴上，点D（-2，3），AD＝5，若反比例函数y＝ $\frac{k}{x}$ （x＞0）的图象经过点B，则k的值为（）

A、4 B、 $\frac{16}{3}$ C、10 D、 $\frac{32}{2}$

查看试题解析

二、填空题（共18分）

11. 如图，用两个可自由转动的转盘做“配紫色”游戏：分别转动两个转盘，若其中一个转出红色，另一个转出蓝色即可配出紫色，那么可配成紫色的概率是.

查看试题解析
12. 如图，大坝横截面的迎水坡AB的坡比为1：2（即BC：AC＝1：2），若坡面AB的水平宽度AC为12米，则斜坡AB的长为米.

查看试题解析
13. 如图，△ABC的顶点是正方形网格的顶点，则sinA的值为.

查看试题解析
14. 已知实数m，n满足m²+3m-2＝0，n²+3n-2＝0，则 $\frac{n}{m} + \frac{m}{n}$ 的值为.

查看试题解析
15. 如图，△OB₁A₁ ， △A₁B₂A₂ ， △A₂B₃A₃ ， …△A_n_-₁B_nA_n均为等边三角形，其中点A₁ ， A₂ ， A₃ ， …A_n都在x轴上，点B₁ ， B₂ ， B₃ ， …，B_n都在反比例函数 $y = \frac{4 \sqrt{3}}{x} (x > 0)$ 的图象上，则A_n的坐标为.

查看试题解析
16. 如图，长方形ABCD中，AB＝3，AD＝4，沿对角线BD折叠，使点A落在点E处，过点E作EF∥CD交BD于点F，连接CF，则CF的长为.

查看试题解析

三、解答题：（共72分）

17. 计算： $\sqrt{12} - (4 - π)^{0} - 2 s i n 6 0^{°} - \sqrt{{(1 - t a n 6 0^{°})}^{2}}$ .

查看试题解析
18. 已知点p（m，n）是反比例函数 $y = \frac{2}{x}$ 图象上一动点，且m≠n，将代数式 $(\frac{1}{m - n} + \frac{1}{m + n}) \div \frac{m^{2} n}{m^{2} - n^{2}}$ 化简并求值.

查看试题解析
19. 为了解市民对全市创卫工作的满意程度，某中学数学兴趣小组在全市甲、乙两个区内进行了调查统计，将调查结果分为不满意，一般，满意，非常满意四类，回收、整理好全部问卷后，得到下列不完整的统计图．
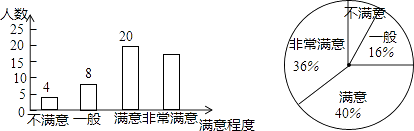
请结合图中信息，解决下列问题：

(1)、求此次调查中接受调查的人数．

(2)、求此次调查中结果为非常满意的人数．

(3)、兴趣小组准备从调查结果为不满意的4位市民中随机选择2位进行回访，已知4位市民中有2位来自甲区，另2位来自乙区，请用列表或用画树状图的方法求出选择的市民均来自甲区的概率．

查看试题解析
20. 已知关于x的方程x²-4x+3a-1＝0有两个实数根.

(1)、求实数a的取值范围；

(2)、若a为正整数，求方程的根.

查看试题解析
21. 如图，海中有两个小岛C、D，某渔船在海中的A处测得小岛D位于东北方向上，且相距30 $\sqrt{2}$ 海里，该渔船自西向东航行一段时间到达B处，此时测得小岛C恰好在点B的正北方向上，且相距75海里，又测得点B与小岛D相距30 $\sqrt{5}$ 海里.

(1)、求sin∠ABD的值；

(2)、求小岛C、D之间的距离（计算过程中的数据不取近似值）.

查看试题解析
22. 如图，点F在平行四边形ABCD的对角线AC上，过点F、B分别作AB、AC的平行线相交于点E，连接BF，已知∠ABF＝∠FBC+∠DAC.

(1)、求证：四边形ABEF是菱形；

(2)、若BE＝6，AD＝10，tan∠CBE＝ $\frac{1}{2}$ ，求AC的长.

查看试题解析
23. 某蔬菜生产基地的气温较低时，用装有恒温系统的大棚栽培一种新品种蔬菜.如图是试验阶段的某天恒温系统从开启到关闭后，大棚内的温度y（℃）与时间x（h）之间的函数关系，其中线段AB、BC表示恒温系统开启阶段，双曲线的一部分CD表示恒温系统关闭阶段.
请根据图中信息解答下列问题：

(1)、求这天的温度y与时间x（0≤x≤24）的函数关系式；

(2)、恒温系统设定的恒定温度为；

(3)、若大棚内的温度低于10℃时，蔬菜会受到伤害.问这天内，为避免蔬菜受到伤害，恒温系统最多可以关闭多少小时？

查看试题解析
24. 已知：如图，一次函数y＝-2x+10的图象与反比例函数y＝ $\frac{k}{x}$ 的图象相交于A、B两点（A在B的右侧），点A横坐标为4.

(1)、求反比例函数解析式及点B的坐标；

(2)、观察图象，直接写出关于x的不等式-2x+10- $\frac{k}{x}$ ＞0的解集；

(3)、反比例函数图象的另一支上是否存在一点P，使△PAB是以AB为直角边的直角三角形？若存在，求出所有符合条件的点P的坐标；若不存在，请说明理由.

查看试题解析
25. 如图

(1)、问题发现：如图1，△ABC是等腰直角三角形，∠BAC＝90°，AB＝AC，四边形ADEF是正方形，点B、C分别在AD、AF上，此时BD与CF的数量关系是，位置关系是；

(2)、拓展探究：如图2，当△ABC绕点A逆时针旋转θ（0°＜θ＜90°）时，BD＝CF成立吗？若成立，请证明；若不成立，请说明理由.

(3)、解决问题：当△ABC绕点A逆时针旋转45°时，如图3，延长BD交CF于点H.已知AB＝2，AD＝ $3 \sqrt{2}$ ，求线段DH的长.

查看试题解析