浙江省温州市鹿城区2022-2023学年九年级上学期期末数学试题

试卷更新日期：2022-12-30 类型：期末考试

进入出卷网下载

一、单选题

1. 已知 $\frac{a}{b} = \frac{2}{3}$ ，则 $\frac{a + b}{b}$ 的值为（）

A、 $\frac{5}{2}$ B、 $\frac{5}{3}$ C、 $\frac{3}{2}$ D、 $\frac{2}{3}$

查看试题解析
2. 两道单选题都含有A、B、C、D四个选项，小明同学在不会做的情况下，两题都答对的概率是(　　)

A、 $\frac{1}{8}$ B、 $\frac{1}{4}$ C、 $\frac{1}{16}$ D、 $\frac{3}{8}$

查看试题解析
3. 抛物线y＝-（x- $\frac{1}{2}$ ）²-2的顶点坐标是（）

A、（ $\frac{1}{2}$ ， 2） B、（- $\frac{1}{2}$ ， 2） C、（- $\frac{1}{2}$ ， -2） D、（ $\frac{1}{2}$ ， -2）

查看试题解析
4. 如图，在⊙O中，AB是弦，OC⊥AB，垂足为C，若AB＝16，OC＝6，则⊙O的半径OA等于（）

A、16 B、12 C、10 D、8

查看试题解析
5. 如图，已知⊙O的直径为4，∠ACB＝45°，则AB的长为（）

A、4 B、2 C、4 $\sqrt{2}$ D、2 $\sqrt{2}$

查看试题解析
6. 如图，在Rt△ABC中，∠ACB＝90°，AC＝24，AB＝25，CD是斜边AB上的高，则cos∠BCD的值为（）

A、 $\frac{7}{25}$ B、 $\frac{24}{25}$ C、 $\frac{7}{24}$ D、 $\frac{24}{7}$

查看试题解析
7. 已知二次函数 $y = 2 m x^{2} + (2 - m) x$ ，它的图象可能是（　　　）

A、 B、 C、 D、

查看试题解析
8. 如图，身高1.5米的小西站在点D处，此时路灯M照射的影子AD为2.5米，小西沿着 $A \to B$ 的方向行走4.5米至点F，此时影子 $N F$ 为1米，则路灯BM的高度为（）

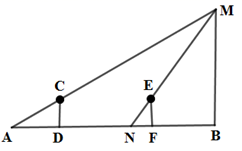A、3米 B、3.5米 C、4.5米 D、6米

查看试题解析
9. 如图，在Rt△ABC中，∠A＝20°，AC＝6，将△ABC绕直角顶点C按顺时针方向旋转得到△A′B′C，当点B′第一次落在AB边上时，点A经过的路径长（即 $\hat{A A'}$ 的长）为（）

A、 $\frac{2}{3} π$ B、 $\frac{4}{3} π$ C、2π D、 $\frac{7}{3} π$

查看试题解析
10. 二次函数y＝ax²+bx+c（a≠0）的大致图象如图所示，顶点坐标为(1，﹣4a)，点A(4，y₁)是该抛物线上一点，若点D(x₂ ， y₂)是抛物线上任意一点，有下列结论：①4a﹣2b+c＞0；②若y₂＞y₁ ，则x₂＞4；③若0≤x₂≤4，则0≤y₂≤5a；④若方程a(x+1)(x﹣3)＝﹣1有两个实数根x₁和x₂ ，且x₁＜x₂ ，则﹣1＜x₁＜x₂＜3．其中正确结论的个数是（）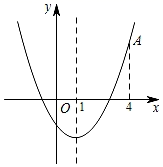

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

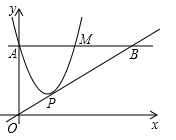
11. 已知抛物线y＝（x+1）²向右平移2个单位，再向上平移1个单位，得到的抛物线表达式为．

查看试题解析
12. 已知一扇形，半径为6，圆心角为120°，则所对的弧长为.

查看试题解析
13. 把只有颜色不同的1个白球和2个红球装入一个不透明的口袋里搅匀，从中随机地摸出1个球后放回搅匀，再次随机地摸出1个球，两次都摸到红球的概率为

查看试题解析
14. 某工厂1月份的产值是200万元，平均每月产值的增长率为 $x (x > 0)$ ，则该工厂第一季度的产值y关于x的函数解析式为.

查看试题解析
15. 如图，在平面直角坐标系中，抛物线 $y = a x^{2} - 2 a x + 3 (a > 0)$ 与y轴交于点A，过点A作x轴的平行线交抛物线于点M，P为抛物线的顶点，若直线OP交直线AM于点B，且M为线段AB的中点，则a的值为.

查看试题解析
16. 如图， $△ A B C$ 内接于 $⊙ O$ ， $∠ B A C = 60 °$ ， D是 $B C$ 的中点，且 $∠ A O D = 166 °$ ， $A E ， C F$ 分别是 $B C ， A B$ 边上的高，则 $∠ B C F$ 的大小 $=$ 度.

查看试题解析

三、解答题

17. 如图，已知△ABO中A（﹣1，3），B（﹣4，0）．

(1)、画出△ABO绕着原点O按顺时针方向旋转90°后的图形，记为△A₁B₁O；

(2)、求第（1）问中线段AO旋转时扫过的面积．

查看试题解析
18. 有A、B、C三种款式的衣服，E、F、G三种款式的裤子，小江任意选一件衣服和一件裤子．

(1)、请用列表法或画树状图的方法表示小江有多少种不同的可能．

(2)、求恰好选中A款衣服和E款裤子的概率．

查看试题解析
19. 如图， $△ A B C$ 中， $A B = A C$ ，以 $A B$ 为直径作⊙O，交 $B C$ 于点 $D$ ，交 $A C$ 于点 $E$ .

(1)、求证： $\overset{⌢}{B D} = \overset{⌢}{D E}$ .

(2)、若 $∠ B A C = 50 °$ ，求 $\overset{⌢}{A E}$ 的度数.

查看试题解析
20. 如图，将矩形ABCD沿EF折叠，使顶点C恰好落在AB边的C₁处，点D落在点D₁处，C₁D₁交线段AE于点G．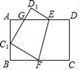

(1)、求证：△BC₁F∽△AGC₁；

(2)、若C₁是AB的中点，AB＝6，BC＝9，求AG的长．

查看试题解析
21. 如图，在矩形 $A B C D$ 中，E是 $B C$ 上一点， $D F ⊥ A E$ 于点F，设 $\frac{A D}{A E} = λ$ $（ λ ＞ 0 ）$ .

(1)、若 $λ = 1$ ，求证： $C E = F E$ ；

(2)、若 $A B = 3$ ， $A D = 4$ ，且D、B、F在同一直线上时，求λ的值.

查看试题解析
22. 已知函数 $y_{1} = (x + m) (x - m - 1)$ ， $y_{2} = a x + m (a \neq 0)$ 在同一平面直角坐标系中.

(1)、若 $y_{1}$ 经过点（1，-2），求 $y_{1}$ 的函数表达式.

(2)、若 $y_{2}$ 经过点（1，m+1），判断 $y_{1}$ 与 $y_{2}$ 图象交点的个数，说明理由.

(3)、若y₁经过点（ $\frac{1}{2}$ ， 0)，且对任意x，都有 $y_{1} > y_{2}$ ，请利用图象求a的取值范围.

查看试题解析
23. 已知钝角三角形 $A B C$ 内接于 $⊙ O ， E 、 D$ 分别为 $A C 、 B C$ 的中点，连接 $D E$ .

(1)、如图1，当点 $A 、 D 、 O$ 在同一条直线上时，求证： $D E = \frac{1}{2} A C$ .

(2)、如图2，当 $A 、 D 、 O$ 不在同一条直线上时，取 $A O$ 的中点 $F$ ，连接 $F D$ 交 $A C$ 于点 $G$ ，当 $A B + A C = 2 A G$ 时.
①求证： $△ D E G$ 是等腰三角形；
②如图3，连 $O D$ 并延长交 $⊙ O$ 于点 $H$ ，连接 $A H$ .求证： $A H ∥ F G$ .

查看试题解析