陕西省西安市2022-2023学年九年级上学期第三次学评数学试卷

试卷更新日期：2022-12-30 类型：月考试卷

进入出卷网下载

一、单选题

1. 一元二次方程 $x^{2} - 2 x = 0$ 的根是（）

A、 $x = 2$ B、 $x = 0$ C、 $x_{1} = 0 ， x_{2} = 2$ D、 $x_{1} = 0 ， x_{2} = - 2$

查看试题解析
2. 如图，矩形 $A B C D$ 中，对角线 $A C 、 B D$ 交于点O，若 $∠ A O B = 60 °$ ， $B D = 8$ ，则 $D C$ 长为（）

A、 $4 \sqrt{3}$ B、4 C、3 D、5

查看试题解析
3. 若 $\frac{x}{y} = \frac{3}{4}$ ，则下列式子不正确的是（）

A、 $\frac{x + y}{y} = \frac{7}{4}$ B、 $\frac{x + 3}{y + 4} = \frac{3}{4}$ C、 $\frac{y}{x - y} = 4$ D、 $\frac{x}{3} = \frac{y}{4}$

查看试题解析
4. 如图： $A B ∥ C D ∥ E F$ ， $A D ： D F = 3 ： 1 ， B E = 12$ ，那么CE的长为（）

A、3 B、4 C、5 D、6

查看试题解析
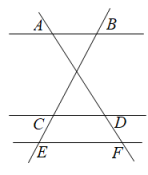5. 已知 $△ A B C ∽ △ A^{'} B^{'} C^{'}$ ， $A D$ 和 $A^{'} D^{'}$ 是它们的对应高线，若 $A D = 4$ ， $A^{'} D^{'} = 2$ ，则 $△ A B C$ 与 $△ A^{'} B^{'} C^{'}$ 的周长比是（）

A、2：1 B、2：3 C、4：1 D、4：9

查看试题解析
6. 若方程 $x^{2} - 2 x - 4 = 0$ 的两个实数根为 $x_{1}$ 、 $x_{2}$ ，则 $(x_{1} - 1) (x_{2} - 1)$ 的值为（）

A、7 B、3 C、－5 D、9

查看试题解析
7. 如图，已知△ABC与△BDE都是等边三角形，点D在边AC上（不与点A、C重合），DE与AB相交于点F，那么与△BFD相似的三角形是（　　　）

A、△BFE； B、△BDC； C、△BDA； D、△AFD．

查看试题解析
8. 菱形的一条对角线长为8，其边长是方程 $x^{2} - 9 x + 20 = 0$ 的一个根，则该菱形的周长为（）

A、40 B、16 C、16或20 D、20

查看试题解析

二、填空题

9. 已知一元二次方程 $x^{2} + 3 x + a^{2} + 1 = 0$ 有一个根为 $x = - 1$ ，则a的值为.

查看试题解析
10. 小颖在地面E处放一面镜子，当他垂直于地面AC站立于点C处时，刚好能从镜子中看到教学楼的顶端B，FE⊥AC，根据光的反射定律有∠FEB=∠FED，此时EA=20米，CE=2.5米．已知眼睛距离地面的高度DC=1.6米，则教学楼的高度为米．

查看试题解析
11. 如图， $△ A B C$ 与 $△ A^{'} B^{'} C^{'}$ 位似，位似中心为点O， $O A = 2 A A^{^{'}}$ ， $△ A B C$ 的面积为4，则 $△ A^{'} B^{'} C^{'}$ 的面积为.

查看试题解析
12. 将矩形OABC如图放置，O为坐标原点，若点A（-1，2），点B的纵坐标是 $\frac{7}{2}$ ，则点C的坐标是.

查看试题解析
13. 如图，在 $△ A B C$ 中， $A B = A C = 4$ ， $∠ C A B = 30 °$ ，以 $A C$ 为斜边作 $R t △ A D C$ .使 $∠ A D C = 90 °$ ， $∠ C A D = ∠ C A B$ ， $E$ 、 $F$ 分别是 $B C$ 、 $A C$ 的中点，连接 $E F$ 、 $D E$ 、 $D F$ ，则 $D E$ 的长为.

查看试题解析

三、解答题

14. 解方程： $x (x + 4) = 8 x + 12$

查看试题解析
15. 如图，在边长为4的正方形ABCD中，P是BC上的点，且BP＝3PC，Q是CD的中点，求证：△ADQ∽△QCP．

查看试题解析
16. 如图，在△ABC中，点D是边AB上的一点，∠ADC=∠ACB，AD=2，BD=6.

(1)、求证：△ACD∽△ABC；

(2)、求边AC的长.

查看试题解析
17. 如图，在边长为1个单位长度的小正方形组成的网格中，给出了格点 $△ A B C$ （顶点是网格线的交点）及平面直角坐标系xOy．

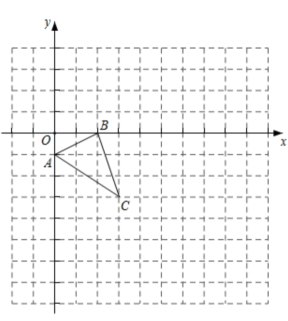(1)、将 $△ A B C$ 绕O点逆时针旋转90°得到 $△ A_{1} B_{1} C_{1}$ ，请画出 $△ A_{1} B_{1} C_{1}$ ；

(2)、以点O为位似中心，在第四象限将 $△ A B C$ 放大2倍得到 $△ A_{2} B_{2} C_{2}$ ，请画出 $△ A_{2} B_{2} C_{2}$ 并求 $△ A_{2} B_{2} C_{2}$ 的面积．

查看试题解析
18. 新冠病毒肆虐全球，我国的疫情很快得到了控制，并且研发出安全性、有效性均非常高的疫苗.经调查发现，北京生物制药厂有1条生产线，最大产能是42万支/天，若每增加1条生产线，每条生产线的最大产能将减少2万支/天，现该厂要保证每天生产疫苗144万支，在既增加产能的同时又节省投入的条件下（生产线越多，投入越大），应该增加几条生产线？

查看试题解析
19. 已知关于x的一元二次方程 $m x^{2} - 6 m x + 9 m - 1 = 0$ 有 $x_{1}$ ， $x_{2}$ 两个实数根．

(1)、求m的取值范围；

(2)、若 $x_{1} = 1$ ，求 $x_{2}$ ．

查看试题解析
20. 如图，已知△ABC中，D是AC的中点，过点D作DE⊥AC交BC于点E，过点A作AF∥BC交DE于点F，连接AE，CF.求证：四边形AECF是菱形.

查看试题解析
21. 在建党100周年之际，老红军谢某打算到学校进行一次党史宣讲活动，初步确定从 $A$ 校、 $B$ 校、 $C$ 校、 $D$ 校、 $E$ 校中随机抽签选取.

(1)、若这次党史宣讲准备选取一所学校，则恰好抽到 $A$ 校的概率是.

(2)、若这次党史宣讲准备选取两所学校，请用画树状图的方法表示出所有可能，并求出所选取的两校恰好是 $A$ 校和 $B$ 校的概率.

查看试题解析
22. 某小队在探险过程途中发现一个深坑，小队人员为了测出坑深，采取如下方案：如图所示，在深坑左侧用观测仪 $A B$ 从观测出发点A观测深坑底部P，且观测视线刚好经过深坑边缘点M，在深坑右侧用观测仪 $C D$ 从观测出发点C观测深坑底部P，且观测视线恰好经过深坑边缘点N.（点E，B，M，N，D，F在同一水平线上）
已知： $A B ⊥ E M ， C D ⊥ N F$ ，观测仪 $A B$ 高 $2 m$ ，观测仪 $C D$ 高 $1 m$ ， $B M = 1.6 m ， N D = 0.8 m$ ，深坑宽度 $M N = 8.8 m$ .请根据以上数据计算深坑深度多少米？

查看试题解析
23. 如图，在平行四边形 $A B C D$ 中，过点 $D$ 作 $D E ⊥ A B$ 于 $E$ ，点 $F$ 在边 $C D$ 上， $D F = B E$ ，连接 $A F$ 、 $B F$ .

(1)、求证：四边形 $B F D E$ 是矩形.

(2)、若 $A F$ 平分 $∠ D A B$ ，且 $D F = 5$ ， $A E = 3$ ，求 $D E$ 的长.

查看试题解析
24. 如图，在菱形ABCD中，点M，N分别是边BC，DC上的点， $∠ E = ∠ B A M$ .连接AM，AN，延长AN交线段BC延长线于点E.

(1)、求证： $△ A B M ≌ △ A D N$ ；

(2)、若 $A D = 5$ ， $C M = 2$ 则ME的长是.

查看试题解析
25. 有长为30米的篱笆，一面利用墙（墙的最大可用长度为10米），围成中间隔有一道篱笆（平行于 $A B$ ）的矩形花圃，设花圃的一边 $A B$ 为 $x$ 米.

(1)、如果要围成面积为63平方米的花圃，那么 $A B$ 的长是多少米？

(2)、能围成面积为78平方米的花圃吗？若能，求出 $A B$ 的长，若不能，请说明理由.

查看试题解析
26. 如图，矩形 $A B C D$ 中， $A B = 15 c m$ ， $B C = 10 c m$ ，动点 $P$ 从点 $A$ 出发，沿 $A B$ 边以 $2 c m / s$ 的速度向点 $B$ 匀速移动，动点 $Q$ 从点 $D$ 出发，沿 $D A$ 边以 $1 c m / s$ 的速度向点 $A$ 匀速移动，一个动点到达端点时，另一个动点也停止运动，点 $P$ ， $Q$ 同时出发，设运动时间为 $t s$ .

(1)、当 $t$ 为何值时， $△ A P Q$ 的面积为 $16 c m^{2}$ ？

(2)、 $t$ 为何值时，以A， $P$ ， $Q$ 为顶点的三角形与 $△ A B C$ 相似.

查看试题解析