吉林省白城市大安市多校联考2022-2023学年九年级上学期第三次月考数学试卷

试卷更新日期：2022-12-30 类型：月考试卷

进入出卷网下载

一、单选题

1. 下列图形是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 下列所给的事件中，是必然事件的是（）

A、随机买一张电影票，座位号是奇数号 B、某校的400名学生中，至少有2名学生的生日是同一天 C、连续4次投掷质地均匀的硬币，会有1次硬币正面朝上 D、2023年的春节假期长春市会下雪

查看试题解析
3. 若关于x的一元二次方程 $x^{2} + 4 x + a = 0$ 有两个相等实数根，则a的值是（）

A、4 B、-4 C、-2 D、2

查看试题解析
4. 若点 $A (3 ， y_{1}) 、 B (0 ， y_{2})$ 是抛物线 $y = {(x - 2)}^{2} + 3$ 上的两点，则 $y_{1} 、 y_{2}$ 的大小关系是（）

A、 $y_{1} > y_{2}$ B、 $y_{1} \geq y_{2}$ C、 $y_{1} < y_{2}$ D、 $y_{1} \leq y_{2}$

查看试题解析
5. 如图， $A B$ 是 $⊙ O$ 的直径，点 $C$ ， $D$ 在圆上， $∠ B A C = 35 °$ ，则 $∠ A D C$ 等于（）

A、 $45 °$ B、 $55 °$ C、 $60 °$ D、 $65 °$

查看试题解析
6. 抛物线 $y = a x^{2} + b x + c$ 经过点 $(1 ， 0)$ ，且对称轴为直线 $x = - 1$ ，其部分图象如图所示，下面结论中正确的是（）

A、 $a b c < 0$ B、 $2 a + b = 0$ C、 $9 a - 3 b + c = 0$ D、 $4 a + 2 b + c > 0$

查看试题解析

二、填空题

7. 一元二次方程 $x^{2} + x - 2 = 0$ 的根的判别式的值为．

查看试题解析
8. 若抛物线y＝（a－1）x²（a为常数）开口向上，则a的取值范围是．

查看试题解析
9. 如图，四边形 $A B C D$ 为 $⊙ O$ 的内接四边形，若 $∠ A D C = 85 °$ ，则 $∠ B =$ ．

查看试题解析
10. 如图，在 $△ A B C$ 中，P为 $B C$ 边上一点．连接 $A P$ ，将线段 $A P$ 绕点A顺时针旋转 $120 °$ 至 $A P^{^{'}}$ ．连接 $P P^{'}$ ，则 $∠ P^{'} =$ ．

查看试题解析
11. 在一个不透明的盒子里装有5个黑色棋子和若干白色棋子，每个棋子除颜色外都相同，任意摸出一个棋子，记下颜色后再放回盒子，通过大量重复摸棋实验后发现，摸到黑色棋子的频率稳定在20%，估计白色棋子的个数为；

查看试题解析
12. 如图，正五边形 $A B C D E$ 内接于 $⊙ O$ ，则 $∠ D A E =$ ．

查看试题解析
13. 明德洞井中学，龙舞腾盛世，强健学生体魄，传承中华传统龙狮文化，如图，在训练中，龙的尾部由四个同学摆成了一个弧形，这弧形的弧长部分占龙总长的二分之一，已知弧形的半径为2米，圆心角为120°，则整条龙的长是米（结果保留 $π$ ）．

查看试题解析
14. 如图，在平面直角坐标系中，点A在抛物线 $y = x^{2}$ 上，过点A作y轴的垂线，交抛物线于另一点B．点C、D为线段AB的三等分点，分别过点C、D作x轴的垂线，交抛物线于点E、F，连接EF．若CE=16，则线段EF的长为．

查看试题解析

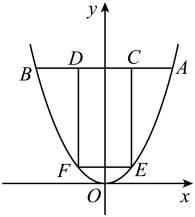
三、解答题

15. 解方程： $x^{2} - 3 x - 5 = 0$

查看试题解析
16. 有3张不透明的卡片，分别标号为A、B、C，它们除正面上的图案不同外，其他均相同．将这3张卡片背面向上洗匀后放在桌面上．若从中随机抽取1张卡片，记下标号后放回洗匀，再随机抽取1张记下标号，请用画树状图或列表的方法求两次所抽取的卡片恰好都是中心对称图形的概率．

查看试题解析
17. 已知二次函数 $y = a x^{2} + b x - 1 (a \neq 0)$ 的图像与 $x$ 轴交于点 $(- 1 ， 0)$ 和 $(4 ， 0)$ ．写出它与 $y$ 轴交点的坐标，并求出它的解析式．

查看试题解析
18. 如图，在 $△ A B C$ 中， $A E$ 平分 $∠ B A C ， B E$ 平分 $∠ A B C ， A E$ 的延长线交 $△ A B C$ 的外接圆于点D，连接 $B D$ ．求证： $D B = D E$ ．

查看试题解析
19. 图①、图②、图③均是4×4的正方形网格，每个小正方形的边长均为1．每个小正方形的顶点叫做格点，△ABC的顶点均在格点上，只用无刻度的直尺，在给定的网格中按要求图，不要求写出画法，保留作图痕迹．

(1)、在图①中画 $△ D E F$ ，使 $△ D E F$ 与 $△ A B C$ 全等，且这两个三角形的对应边互相平行；

(2)、在图②中画 $△ B C G$ ，使 $△ B C G$ 与 $△ A B C$ 关于某条直线对称；

(3)、在图③中画 $△ A B H$ ，使 $△ A B H$ 与 $△ A B C$ 关于某点成中心对称．

查看试题解析
20. 如图，已知二次函数 $y = - x^{2} + b x + c$ 的图像经过点 $A (3 ， 1)$ 、点 $B (0 ， 4)$ ．

(1)、求该二次函数的解析式及顶点坐标；

(2)、已知二次函数的图象与 $x$ 轴交于 $C$ 、 $D$ 两点，求 $△ A C D$ 的面积．

查看试题解析
21. 如图， $A B$ 是 $⊙ O$ 的直径，点C为圆周上一点，连接 $A C 、 B C$ ，点D是 $A B$ 延长线上一点，作 $∠ D C B = ∠ C A B$ ．

(1)、求证： $C D$ 是 $⊙ O$ 的切线；

(2)、若 $∠ A = 30 °$ ， $A B = 6$ ，则CD的长为．

查看试题解析
22. 在美化校园的活动中，某兴趣小组想借助如图所示的直角墙角（两边足够长）、用 $28 m$ 长的篱笆围成一个矩形花园 $A B C D$ （篱笆只围 $A B ， B C$ 两边），设 $A B = x m$ ，花圈的面积为 $S m^{2}$ ．

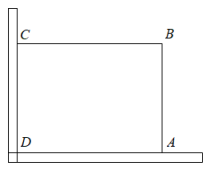(1)、若花园的面积为 $192 m^{2}$ ，求x的值；

(2)、写出花园面积S与x的函数关系式，并求当x为何值时，花园面积S有最大值？最大值为多少？

查看试题解析
23. 如图，以 $△ A B C$ 的边 $A B$ 为直径作 $⊙ O$ ，交 $B C$ 于 $D$ 点，交 $A C$ 于 $E$ 点， $B D = D E$ ．

(1)、求证： $△ A B C$ 是等腰三角形；

(2)、若 $E$ 是 $A C$ 的中点， $⊙ O$ 的半径为2，连接 $B E$ ，求阴影部分的面积（结果保留 $π$ ）．

查看试题解析
24. 如图①，在 $△ A B C$ 中， $A B = A C$ ， $∠ B A C = a$ ， D为 $B C$ 边上一点（不与点B、C重合），将线段 $A D$ 绕点A逆时针旋转a，得到 $A E$ ，连接 $D E$ 、 $C E$ ．

(1)、求证： $C E = B D$ ；

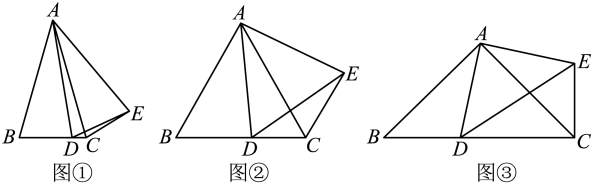(2)、若 $a = 60 °$ ，其他条件不变，如图②，线段 $A C$ 、 $C D$ 、 $C E$ 之间的数量关系为（不用证明）；

(3)、若 $a = 90 °$ ，其他条件不变，如图③，线段 $A D$ 、 $B D$ 、 $C D$ 之间的数量关系为（不用证明）．

查看试题解析
25. 如图，在等腰直角三角形 $A B C$ 中， $∠ A C B = 90 °$ ， $A B = 8 \sqrt{2} c m$ ，点 $P$ （不与 $A$ ， $B$ 重合）从点 $A$ 出发，沿 $A B$ 方向以 $\sqrt{2}$ cm/s的速度向终点 $B$ 运动，在运动过程中，过点 $P$ 作 $P Q ⊥ A B$ 交射线 $B C$ 于点 $Q$ ，以线段 $P Q$ 为边作等腰直角三角形 $P Q R$ ，且 $∠ P Q R = 90 °$ （点 $B$ ， $R$ 位于 $P Q$ 两侧），设 $△ P Q R$ 与 $Δ A B C$ 重叠部分图形的面积为S（cm²），点 $P$ 的运动时间为t（s）．

(1)、当点 $Q$ 与点 $C$ 重合时，t=；

(2)、求 $S$ 与 $t$ 之间的函数关系式；

(3)、直接写出直线 $C R$ 平分 $△ A B C$ 面积时 $t$ 的值．

查看试题解析
26. 如图，在平面直角坐标系中，抛物线 $y = \frac{1}{2} x^{2} + b x + c$ （b，c为常数）的顶点坐标为 $(\frac{3}{2} ， - \frac{25}{8})$ ，与x轴交于A、B两点（点A在点B左侧），与y轴交于点C，点C、点D关于x轴对称，连接 $A D$ ，作直线 $B D$ ．

(1)、求b、c的值；

(2)、求点A、B的坐标；

(3)、求直线 $B D$ 的解析式；

(4)、点P在抛物线上，点Q在直线 $B D$ 上，当以点C、D、P、Q为顶点的四边形为平行四边形时，直接写出点Q的坐标．

查看试题解析