广东省佛山市南海区2022-2023学年九年级上学期12月月考数学试题

试卷更新日期：2022-12-30 类型：月考试卷

进入出卷网下载

一、单选题

1. 在下面的四个几何体中，左视图与主视图不相同的几何体是（）

A、正方体 B、圆柱 C、直三棱柱 D、圆锥

查看试题解析
2. 用配方法解方程 $x^{2} - 6 x + 7 = 0$ ，配方后的方程是（）

A、 $(x + 3)^{2} = 7$ B、 $(x - 3)^{2} = 7$ C、 $(x - 3)^{2} = 2$ D、 $(x + 3)^{2} = 2$

查看试题解析
3. 对于反比例函数 $y = - \frac{2}{x}$ ，下列说法错误的是（）

A、点 $(- 2 ， 1)$ 在它的图象上 B、当 $x > 0$ 时 $y$ 随 $x$ 的增大而增大 C、它的图象在第二、四象限 D、若点 $A (x_{1} ， y_{1})$ ， $B (x_{2} ， y_{2})$ 都在图象上，且 $x_{1} < x_{2}$ ，则 $y_{1} < y_{2}$

查看试题解析
4. 晚上，人在马路上走过一盏路灯的过程中，其影子长度的变化情况是（）

A、先变短后变长 B、先变长后变短 C、逐渐变短 D、逐渐变长

查看试题解析
5. 已知关于x的一元二次方程(k－1)x²－2x＋1＝0有两个实数根，则k的取值范围是（）

A、k≤-2 B、k≤2 C、k≥2 D、k≤2且k≠1

查看试题解析
6. 从甲、乙、丙、丁四名同学中随机选取两名去参加“喜迎二十大”演讲比赛，则恰好抽到乙、丁两位同学的概率是（）

A、 $\frac{1}{8}$ B、 $\frac{1}{6}$ C、 $\frac{1}{4}$ D、 $\frac{1}{2}$

查看试题解析
7. 如图，在平行四边形 $A B C D$ 中． $E$ 为CD上一点． $D E ： C E = 2 ： 3$ ．连接AE，BD交于点 $F$ ，则 $S_{△ D E F} ： S_{△ A B F}$ 等于（）

A、2：5 B、2：25 C、4：5 D、4：25

查看试题解析
8. 已知菱形的面积为 $120 c m^{2}$ ，一条对角线长为 $10 c m$ ，则它的边长为（）

A、 $10 c m$ B、 $12 c m$ C、 $13 c m$ D、 $15 c m$

查看试题解析
9. 如图，将长方形 $A B C D$ 沿对角线 $B D$ 折叠，得到 $△ B D E$ ，点 $C$ 与点 $E$ 对应， $B E$ 交 $A D$ 于 $F$ ，若 $A D = 8$ ， $E F = 3$ ，则 $D F$ 的长为（）

A、5 B、6 C、 $\frac{13}{2}$ D、 $3 \sqrt{3}$

查看试题解析
10. 如图，在平面直角坐标系中，直线 $y = - \frac{2}{3} x$ 与直线 $y = - \frac{2}{3} x + 2$ 分别与函数 $y = \frac{k}{x}$ $(x < 0)$ 的图象交点 $A$ 、 $B$ 两点，连结 $A B$ 、 $O B$ ，若 $△ O A B$ 的面积为 $3$ ，则 $k$ 的值为（）．

A、-2 B、-3 C、-4 D、-6

查看试题解析

二、填空题

11. 已知k是一元二次方程 $x^{2} - x - 2 = 0$ 的一个根，则 $k^{2} - k =$ .

查看试题解析
12. 不透明的袋子中装有8个球，除颜色外无其他差别．每次把球充分搅匀后，随机摸出一个球记下颜色再放回袋子．通过大量重复试验，发现摸到白球的频率稳定于0.25，则袋子中白球的个数约是．

查看试题解析
13. △AOB的顶点坐标分别为A(4，2)、B(3，0)、O(0，0)．若以原点O为位似中心将图形放大2倍，则点A的对应点的坐标为．

查看试题解析
14. 反比例函数 $y = \frac{k}{x}$ 的图像经过点（4，3），若x＞2，则y的取值范围是．

查看试题解析
15. 如图，菱形ABCD中，AB＝2，∠A＝120°，点P是直线BD上一动点，连接PC，当PC＋ $\frac{P B}{2}$ 的值最小时，线段PD的长是．

查看试题解析

三、解答题

16. 解方程：x（5x+4）＝5x+4．

查看试题解析
17. 如图，在△ABC中， $A B = A C$ ，点P在BC上．在线段AC上求作一点D，使 $△ P C D ∽ △ A B P$ ．（保留作图痕迹，不写作法）

查看试题解析
18. 利用镜面反射可以计算旗杆的高度，如图，一名同学（用AB表示），站在阳光下，通过镜子C恰好看到旗杆ED的顶端，已知这名同学的身高是1.60米，他到镜子的距离是2米，镜子到旗杆的距离是8米，求旗杆的高．

查看试题解析
19. 中国空间站作为国家太空实验室，也是重要的太空科普教育基地.2022年3月23日“天宫课”中航天员生动演示了微重力环境下的4个实验，分别是A．太空冰雪实验、B．液桥演示实验、C．水油分离实验、D．太空抛物实验．某中学开展这4个实验为主题的手抄报评比活动，学生会随机抽取部分同学调查他们所感兴趣的主题，数据如下：
根据图中提供的信息，解答下列问题：

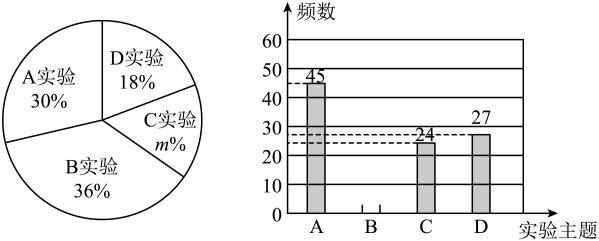(1)、学生会随机调查了名同学；

(2)、补全频数分布直方图；

(3)、扇形中m= ， A实验所对应的圆心角为；

(4)、若4个实验任选其一为主题设计手抄报，利用树状图或列表的方法求大华和小宇选取不同实验的概率．

查看试题解析
20. 某校“研学”活动小组在一次野外实践时，发现一种植物的主干长出若干数目的支干，每个支干又长出同样数目的小分支，主干、支干和小分支的总数是43，求这种植物每个支干长出的小分支个数

查看试题解析
21. 如图，在 $△ A B C$ 中， $∠ B A C = 90 °$ ， AD是中线，E是AD的中点，过点A作 $A F ∥ B C$ 交BE的延长线于F，连接CF．

(1)、求证： $B D = A F$ ；

(2)、如果 $A B = A C$ ，试判断四边形ADCF的形状并证明．

查看试题解析
22. 如图，在平面直角坐标系中，矩形 $A B C D$ 的顶点 $B$ 、 $C$ 在 $x$ 轴的正半轴上， $A B = 8$ ， $B C = 6$ ．对角线 $A C$ ， $B D$ 相交于点 $E$ ，反比例函数 $y = \frac{k}{x} (x > 0)$ 的图象经过点 $E$ ，分别与 $A B$ ， $C D$ 交于点 $F$ ， $G$ ．

(1)、若 $O C = 10$ ，求 $k$ 的值；

(2)、连接 $E G$ ，若 $B F + B E = 11$ ，求 $△ C E G$ 的面积．

查看试题解析
23. 如图，在 $△ A B C$ 中， $∠ C = 90 °$ ， $A C = 6$ ， $B C = 8$ ， $D$ 是 $B C$ 边的中点， $E$ 为 $A B$ 边上的一个动点，作 $∠ D E F = 90 °$ ， $E F$ 交射线 $B C$ 于点 $F$ ．设 $B E = x$ ， $△ B E D$ 的面积为 $y$ ．

(1)、求 $y$ 关于 $x$ 的函数关系式，并写出自变量 $x$ 的取值范围；

(2)、如果以 $B$ 、 $E$ 、 $F$ 为顶点的三角形与 $△ B E D$ 相似，求 $△ B E D$ 的面积．

查看试题解析