广东省佛山市里水镇2022--2023学年九年级上学期第三次质量监测数学试题
试卷更新日期:2022-12-30 类型:月考试卷
一、单选题
-
1. 下列四个函数中是二次函数的是( )A、 B、 C、 D、2. 某学校在八年级开设了数学史、诗词赏析、陶艺三门课程,若小波和小睿两名同学每人随机选择其中一门课程,则小波和小睿选到同一门课程的概率是( )A、 B、 C、 D、3. 如图所示的几何体的左视图是( )
 A、
A、 B、
B、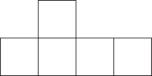 C、
C、 D、
D、 4. 在△ABC中,∠C=90°,AC=6,cosA= ,则BC的长为( )A、6 B、8 C、10 D、95. 若点 , 都在二次函数的图象上,则a与b的大小关系是( )A、 B、 C、 D、无法确定6. 若反比例函数y= 图象经过点(5,-1),该函数图象在( )A、第一、二象限 B、第一、三象限 C、第二、三象限 D、第二、四象限7. 若一元二次方程x2-2x+k=0有两个不相等的实数根,则k的取值范围是( )A、k>1 B、k<1 C、k<1且k≠0 D、k≥18. 在同一直角坐标系中,函数y=kx+1与y=﹣ (k≠0)的图象大致是( )A、
4. 在△ABC中,∠C=90°,AC=6,cosA= ,则BC的长为( )A、6 B、8 C、10 D、95. 若点 , 都在二次函数的图象上,则a与b的大小关系是( )A、 B、 C、 D、无法确定6. 若反比例函数y= 图象经过点(5,-1),该函数图象在( )A、第一、二象限 B、第一、三象限 C、第二、三象限 D、第二、四象限7. 若一元二次方程x2-2x+k=0有两个不相等的实数根,则k的取值范围是( )A、k>1 B、k<1 C、k<1且k≠0 D、k≥18. 在同一直角坐标系中,函数y=kx+1与y=﹣ (k≠0)的图象大致是( )A、 B、
B、 C、
C、 D、
D、 9. 如图,在△ABC中,点D,E分别在边AB,AC上, , 若CE=2AE,则( )
9. 如图,在△ABC中,点D,E分别在边AB,AC上, , 若CE=2AE,则( ) A、 B、 C、 D、10. 如图,在△ABC中,AD=AC,延长CD至B,使BD=CD,DE⊥BC交AB于点E,EC交AD于点F.下列四个结论:①EB=EC;②BC=2AD;③△ABC∽△FCD;④若AC=6,则DF=3.其中正确的个数有( )
A、 B、 C、 D、10. 如图,在△ABC中,AD=AC,延长CD至B,使BD=CD,DE⊥BC交AB于点E,EC交AD于点F.下列四个结论:①EB=EC;②BC=2AD;③△ABC∽△FCD;④若AC=6,则DF=3.其中正确的个数有( ) A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
11. 若 ,则 .12. 一只不透明的袋子中装有红球和白球共30个,这些球除了颜色外都相同,校课外学习小组做摸球试验,将球搅匀后任意摸出一个球,记下颜色后放回、搅匀,通过多次重复试验,算得摸到红球的频率是20%,则袋中有红球个数是 .13. 若 , , 的面积为 , 则的面积为14. 若m是方程的一个根,则的值为 .15. 如图,菱形ABCD的对角线AC,BD相交于点O,过点D作于点H,连接OH,若 , , 则菱形ABCD的面积为 .

三、解答题
-
16.(1)、计算: .(2)、解方程: .17. 为做好疫情防控工作,确保师生生命安全,学校每日都在学生进校前进行体温检测.某学校大门高6.5米,学生身高1.5米,当学生准备进入体温检测有效识别区域时,在点D处测得摄像头A的仰角为 , 当学生刚好离开体温检测有效识别区域段时,在点C处测得摄像头A的仰角为 , 求体温检测有效识别区域段的长(结果保留根号)
 18. 如图,D是AC上一点,DE∥AB,∠B=∠DAE.
18. 如图,D是AC上一点,DE∥AB,∠B=∠DAE. (1)、求证:△ABC∽△DAE;(2)、若AB=4,AD=3,AE=6,求BC的长.19. 如图,正方形ABCD,点P在边BC的延长线上,连接AP交BD于点F,过点C作CG//AP交BD于点G,连接AG、CF.
(1)、求证:△ABC∽△DAE;(2)、若AB=4,AD=3,AE=6,求BC的长.19. 如图,正方形ABCD,点P在边BC的延长线上,连接AP交BD于点F,过点C作CG//AP交BD于点G,连接AG、CF. (1)、求证:△ADF≌△CBG;(2)、判断四边形AGCF是什么特殊四边形?请说明理由.20. 目前新型冠状病毒变种奥密克戎,仍在全世界范围肆虐.在我国疫情中高风险地区,仍需要采取以下防护措施:戴口罩;勤洗手;少聚集;重隔离;打疫苗等.某公司为了解员工对防护措施的了解程度(包括不了解、了解很少、基本了解和很了解),通过网上问卷调查的方式进行了随机抽样调查(每名员工必须且只能选择一项),并将调查结果绘制如下两幅统计图.
(1)、求证:△ADF≌△CBG;(2)、判断四边形AGCF是什么特殊四边形?请说明理由.20. 目前新型冠状病毒变种奥密克戎,仍在全世界范围肆虐.在我国疫情中高风险地区,仍需要采取以下防护措施:戴口罩;勤洗手;少聚集;重隔离;打疫苗等.某公司为了解员工对防护措施的了解程度(包括不了解、了解很少、基本了解和很了解),通过网上问卷调查的方式进行了随机抽样调查(每名员工必须且只能选择一项),并将调查结果绘制如下两幅统计图.
请你根据上面的信息,解答下列问题
(1)、本次共调查了名员工,条形统计图中;(2)、若该公司共有员工1000名,请你估计对防护措施达到“基本了解”和“很了解”程度的员工总人数;(3)、在调查中,发现有4名员工对防护措施“很了解”,其中有3名男员工、1名女员工.若准备从他们中随机抽取2名,让其在公司群内普及防护措施,用画树状图或列表法求恰好抽中一男一女的概率(要求画出树状图或列出表格).21. “玫瑰香”葡萄品种是农科院研制的优质新品种,在被广泛种植,某葡萄种植基地2019年种植64亩,到2021年的种植面积达到100亩.(1)、求该基地这两年“玫瑰香”种植面积的平均增长率.(2)、某超市调查发现,当“玫瑰香”的售价为8元/千克时,每周能售出400千克,售价每上涨1元,每周销售量减少20千克,已知该超市“玫瑰香”的进价为6元/千克,为了维护消费者利益,物价部门规定,该水果售价不能超过15元.若使销售“玫瑰香”每周获利2240元,则售价应上涨多少元?22. 如图,一次函数的图象与反比例函数的图象交于点 , 与y轴交于点B.
 (1)、求a,k的值;(2)、直线CD过点A,与反比例函数图象交于点C,与x轴交于点D,AC=AD,连接CB.
(1)、求a,k的值;(2)、直线CD过点A,与反比例函数图象交于点C,与x轴交于点D,AC=AD,连接CB.①求△ABC的面积;
②点P在反比例函数的图象上,点Q在x轴上,若以点A,B,P,Q为顶点的四边形是平行四边形,请求出所有符合条件的点P坐标.
23. 如图,在中, , 于点D,且 . 点M从点A出发,沿的方向匀速运动,速度为;同时直线由点B出发,沿的方向匀速运动,速度为 , 运动过程中始终保持 , 直线交于点P、交于点Q、交于点F.连接 , 设运动时间为 . (1)、填空:cm,cm(用含t的代数式表示)(2)、当t为何值时,四边形是平行四边形?(3)、连接 , 是否存在某一时刻t,使点M在线段的垂直平分线上?若存在,求出此时t的值;若不存在,说明理由.
(1)、填空:cm,cm(用含t的代数式表示)(2)、当t为何值时,四边形是平行四边形?(3)、连接 , 是否存在某一时刻t,使点M在线段的垂直平分线上?若存在,求出此时t的值;若不存在,说明理由.