北京市通州区北关中学2022-2023学年九年级上学期数学第三次月考测试题

试卷更新日期：2022-12-30 类型：月考试卷

进入出卷网下载

一、单选题

1. 中国传统扇文化有着深厚的底蕴，下列扇面图形是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 方程x²﹣x=0的解是（）

A、x=0 B、x=1 C、x₁=0，x₂=﹣1 D、x₁=0，x₂=1

查看试题解析
3. 有一个可以自由转动且质地均匀的转盘，被分成6 个大小相同的扇形．在转盘的适当地方涂上灰色，未涂色部分为白色．为了使转动的转盘停止时，指针指向灰色的概率为 $\frac{2}{3}$ ，则下列各图中涂色方案正确的是（　　）

A、 B、 C、 D、

查看试题解析
4. 下列关于二次函数y＝2x²的说法正确的是（）

A、它的图象经过点（-1，-2） B、当x＜0时，y随x的增大而减小 C、它的图象的对称轴是直线x＝2 D、当x＝0时，y有最大值为0

查看试题解析
5. 如图，△ABC∽△A′B′C′，AD 和 A′D′分别是△ABC 和△A′B′C′的高，若 AD＝2，A′D′＝3，则△ABC 与△A′B′C′的面积的比为（）

A、4：9 B、9：4 C、2：3 D、3：2

查看试题解析
6. 如图，在平面直角坐标系xOy中，以原点O为位似中心，把线段AB放大后得到线段CD．若点A（1，2），B（2，0），D（5，0），则点A的对应点C的坐标是（）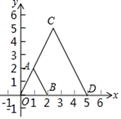

A、(2，5) B、( $\frac{5}{2}$ ，5) C、(3，5) D、(3，6)

查看试题解析
7. 如图，数轴上有A，B，C三点，点A，C关于点B对称，以原点O为圆心作圆，若点A，B，C分别在 $⊙ O$ 外， $⊙ O$ 内， $⊙ O$ 上，则原点O的位置应该在（）

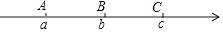A、点A与点B之间靠近A点 B、点A与点B之间靠近B点 C、点B与点C之间靠近B点 D、点B与点C之间靠近C点

查看试题解析
8. 如图，AB是半圆O的直径，按以下步骤作图：
（1）分别以A，B为圆心，大于AO长为半径作弧，两弧交于点P，连接OP与半圆交于点C；（2）分别以A，C为圆心，大于 $\frac{1}{2}$ AC长为半径作弧，两弧交于点Q，连接OQ与半圆交于点D；（3）连接AD，BD，BC，BD与OC交于点 E．根据以上作图过程及所作图形，下列结论：①BD平分∠ABC；②BC∥OD；③CE＝OE；④AD²＝OD•CE；所有正确结论的序号是（）

A、①② B、①④ C、②③ D、①②④

查看试题解析

二、填空题

9. 如图，△ABC中，点D，E分别在AB，AC边上，DE∥BC，若AD＝2，DB＝3，DE＝1，则BC的长是．

查看试题解析
10. 如图，点A、B、C、D、O都在方格纸上，若△COD是由△AOB绕点O按逆时针方向旋转而得，则旋转的角度为．

查看试题解析
11. 已知反比例函数y= $\frac{m - 2}{x}$ ，当x＞0时，y随x增大而减小，则m的取值范围是．

查看试题解析
12. 若一个扇形的半径为3，圆心角是120°，则它的面积是．

查看试题解析
13. 小宇调查了初一年级三个班学生的身高，并进行了统计，列出如频数分布表：若要从每个班级中选取10名身高在 $160 c m$ 和 $170 c m$ 之间同学参加学校的广播操展示，不考虑其他因素的影响，则（填“1班”，“2班”或“3班”）的可供挑选的空间最大．
身高/厘米
频数
班级
$150 \leq x < 155$
$155 \leq x < 160$
$160 \leq x < 165$
$165 \leq x < 170$
$170 \leq x < 175$
合计
1班
1
8
12
14
5
40
2班
10
15
10
3
2
40
3班
5
10
10
8
7
40

查看试题解析
14. 如图，在平面直角坐标系xOy中，函数y＝ $\frac{2}{x}$ （x＞0）的图象经过点A，B，AC⊥x轴于点C，BD⊥y轴于点D，连接OA，OB，则△OAC与△OBD的面积之和为.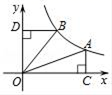

查看试题解析
15. 测量附中国旗杆的高度，小宇的测量方法如下：如图，将直角三角形硬纸板△DEF的斜边DF与地面保持平行，并使边DE与旗杆顶点A在同一直线上．测得DE＝0.5米，EF＝0.25米，目测点D到地面的距离DG＝1.6米，到旗杆的水平距离DC＝18米．按此方法，可计算出旗杆的高度为米．

查看试题解析
16. 如图，在Rt△ABC中，∠C＝90°，记x＝AC，y＝BC-AC，在平面直角坐标系xOy中，定义（x，y）为这个直角三角形的坐标，Rt△ABC为点（x，y）对应的直角三角形．有下列结论：①在x轴正半轴上的任意点（x，y）对应的直角三角形均满足AB＝ $\sqrt{2}$ BC；②在函数y＝ $\frac{2019}{x}$ （x＞0）的图象上存在两点P，Q，使得它们对应的直角三角形相似；③对于函数y＝（x-2020）²-1（x＞0）的图象上的任意一点P，都存在该函数图象上的另一点Q，使得这两个点对应的直角三角形相似；④在函数y＝-2x+2020（x＞0）的图象上存在无数对点P，Q（P与Q不重合），使得它们对应的直角三角形全等．所有正确结论的序号是．

查看试题解析

三、解答题

17. 解方程：x²-2x＝2（x+1）．

查看试题解析
18. 如图，已知∠B＝∠C＝90°，点E在BC上，且满足AB＝4，BE＝2，CE＝6，CD＝3．求证：AE⊥DE．

查看试题解析
19. 已知二次函数 $y = x^{2} - 4 x + 3$ ．

(1)、把二次函数化成 $y = a (x - h)^{2} + k$ 的形式；

(2)、在平面直角坐标系xOy中画出该函数的图象；

(3)、当0≤x≤3时，y的取值范围是．

查看试题解析
20. 如图，四边形ABCD内接于⊙O，OC＝2，AC＝2 $\sqrt{2}$ ．

(1)、求点O到AC的距离；

(2)、求∠ADC的度数．

查看试题解析
21. 某市计划建设一项水利工程，运输公司接到任务后，计划每天运输土方2000 $m^{3}$ ，共计50天运完，但由于受到各种因素的影响，实际平均每天运输土方v $m^{3}$ ，共计t天运输完成．

(1)、请直接写出v关于t的函数关系式；

(2)、为了给后续工程节省出时间，这批土方需要在40天内运输完成，求实际平均每天至少需要比原计划增加多少土方运输量？

查看试题解析
22. 已知关于x的一元二次方程 $\frac{1}{4}$ x²+bx+c＝0．

(1)、c＝2b-1时，求证：方程一定有两个实数根．

(2)、有甲、乙两个不透明的布袋，甲袋中装有3个除数字外完全相同的小球，分别标有数字1，2，3，乙袋中装有4个除数字外完全相同的小球，分别标有数字1，2，3，4，从甲袋中随机抽取一个小球，记录标有的数字为b，从乙袋中随机抽取一个小球，记录标有的数字为c，利用列表法或者树状图，求b、c的值使方程 $\frac{1}{4}$ x²+bx+c＝0有两个相等的实数根的概率．

查看试题解析
23. 如图，在平面直角坐标系xOy中，直线l：y＝kx-1（k≠0）与函数y＝ $\frac{m}{x}$ （x＞0）的图象交于点A（3，2）．

(1)、求k，m的值；

(2)、将直线l沿y轴向上平移t（t＞0）个单位后，所得直线与x轴，y轴分别交于点P，Q，与函数y＝ $\frac{m}{x}$ （x＞0）的图象交于点C．
①当t＝2时，求线段QC的长；
②若2＜ $\frac{Q C}{P Q}$ ＜3，结合函数图象，直接写出t的取值范围．

查看试题解析
24. 如图，在弧 $A B$ 和弦 $A B$ 所组成的图形中，P是弦 $A B$ 上一动点，过点P作弦 $A B$ 的垂线，交弧 $A B$ 于点C，连接 $A C$ ．已知 $A B = 6 c m$ ，设A，P两点间的距离为 $x c m$ ， P，C两点间的距离为 $y_{1} c m$ ， A，C两点间的距离为 $y_{2} c m$ ．
小宇根据学习函数的经验，分别对函数 $y_{1} ， y_{2}$ 随自变量x的变化而变化的规律进行了探究．下面是小宇的探究过程，请补充完整：

(1)、按照下表中自变量x的值进行取点、画图、测量，分别得到了 $y_{1} ， y_{2}$ 与x的几组对应值： $x / c m$
x/cm
0
1
2
3
4
5
6
y₁/cm
0
2.24
2.83
3.00
2.83
2.24
0
y₂/cm
0
2.45
3.46
4.24
5.48
6

(2)、在同一平面直角坐标系 $x O y$ 中，描出补全后的表中各组数值所对应的点 $(x ， y_{1}) ， (x ， y_{2})$ ，并画出函数 $y_{1} ， y_{2}$ 的图象；

(3)、结合函数图象，解决问题：当 $△ A P C$ 有一个角是 $60 °$ 时， $A P$ 的长度约为

查看试题解析
25. 如图， $⊙ O$ 是 $△ A B C$ 的外接圆，直径 $B D$ 与 $A C$ 交于点E，过点D作 $⊙ O$ 的切线，与 $B C$ 的延长线交于点F．

(1)、求证： $∠ F = ∠ B A C$ ；

(2)、若 $D F ∥ A C$ ，若 $A B = 8$ ， $C F = 2$ ，求 $A C$ 的长．

查看试题解析
26. 在平面直角坐标系 $x O y$ 中，抛物线 $y = x^{2} - 2 a x + a^{2} - a + 4$ 的顶点为A，点B，C为直线 $y = 3$ 上的两个动点（点B在点C的左侧），且 $B C = 3$ ．

(1)、求点A的坐标（用含a的代数式表示）；

(2)、若 $△ A B C$ 是以 $B C$ 为直角边的等腰直角三角形，求抛物线的解析式；

(3)、过点A作x轴的垂线，交直线 $y = 3$ 于点D，点D恰好是线段BC三等分点且满足 $B C = 3 B D$ ，若抛物线与线段 $B C$ 只有一个公共点，结合函数的图象，直接写出a的取值范围．

查看试题解析
27. 如图，在Rt△ABC中，∠ACB＝90°，点C关于直线AB的对称点为D，连接BD，CD，过点B作BE∥AC交直线AD于点E．

(1)、依题意补全图形；

(2)、找出一个图中与△CDB相似的三角形，并证明；

(3)、延长BD交直线AC于点F，过点F作FH∥AE交直线BE于点H，请补全图形，猜想BC，CF，BH之间的数量关系并证明．

查看试题解析
28. 新定义：在平面直角坐标系xOy中，若几何图形G与⊙A有公共点，则称几何图形G为⊙A的关联图形，特别地，若⊙A的关联图形G为直线，则称该直线为⊙A的关联直线．如图1，∠M为⊙A的关联图形，直线l为⊙A的关联直线．

(1)、已知⊙O是以原点为圆心，2为半径的圆，下列图形：
①直线y＝2x+2；②直线y＝-x+3；③双曲线y＝ $\frac{2}{x}$ ，是⊙O的关联图形的是（请直接写出正确的序号）．

(2)、如图2，⊙T的圆心为T（1，0），半径为1，直线l：y＝-x+b与x轴交于点N，若直线l是⊙T的关联直线，求点N的横坐标的取值范围．

(3)、如图3，已知点B（0，2），C（2，0），D（0，-2），⊙I经过点C，⊙I的关联直线HB经过点B，与⊙I的一个交点为P；⊙I的关联直线HD经过点D，与⊙I的一个交点为Q；直线HB，HD交于点H，若线段PQ在直线x＝6上且恰为⊙I的直径，请直接写出点H横坐标h的取值范围．

查看试题解析

身高/厘米频数班级	$150 \leq x < 155$	$155 \leq x < 160$	$160 \leq x < 165$	$165 \leq x < 170$	$170 \leq x < 175$	合计
1班	1	8	12	14	5	40
2班	10	15	10	3	2	40
3班	5	10	10	8	7	40

x/cm	1	2	3	4	5	6
y₁/cm	2.24	2.83	3.00	2.83	2.24	0
y₂/cm	2.45	3.46	4.24		5.48	6