安徽省蒙城县2022-2023学年九年级上学期质量调研三数学试卷

试卷更新日期：2022-12-30 类型：月考试卷

进入出卷网下载

一、单选题

1. 若∠A为锐角，且sinA＝ $\frac{\sqrt{3}}{2}$ ，则cosA的值是（）

A、1 B、 $\frac{\sqrt{3}}{2}$ C、 $\frac{\sqrt{2}}{2}$ D、 $\frac{1}{2}$

查看试题解析
2. 对于二次函数y＝3（x-2）²+1的图象，下列说法正确的是（）

A、开口向下 B、对称轴是直线x＝-2 C、顶点坐标是（2，1） D、与x轴有两个交点

查看试题解析
3. 在Rt△ABC中，∠C=90°，AB=5，AC=4．下列四个选项，正确的是（）

A、tanB= $\frac{3}{4}$ B、sinB= $\frac{4}{3}$ C、sinB= $\frac{4}{5}$ D、cosB= $\frac{4}{5}$

查看试题解析
4. 如图，一块等腰直角三角板，它的斜边BC=8cm，内部△DEF的各边与△ABC的各边分别平行，且它的斜边EF=4cm，则△DEF 的面积与阴影部分的面积比为（）

A、1：2 B、1：3 C、1：4 D、1：8

查看试题解析
5. 如图，DE∥BC，且EC：BD=2：3，AD=6，则AE的长为（）

A、1 B、2 C、3 D、4

查看试题解析
6. 一次函数y₁=mx+n(m≠0)与二次函数y₂=ax²+bx+c(a≠0)的图象如图所示，则不等式ax²+bx+c＞mx+n的解集为（）

A、3＜x＜－4 B、x＜－4 C、－4＜x＜3 D、x ＞3或x＜－4

查看试题解析
7. 已知 $\frac{1}{2}$ <cosA< sin80° ，则锐角A的取值范围是（）

A、60°<A<80° B、30°<A<80° C、10°<A<60° D、10°<A<30°

查看试题解析
8. 如图，等腰三角形 $△$ ABC的顶点A在原点固定，且始终有 $A C = B C$ ，当顶点C在函数 $y = \frac{k}{x} (x > 0)$ 的图象上从上到下运动时，顶点B在x轴的正半轴上移动，则 $△$ ABC的面积大小变化情况是（）

A、先减小后增大 B、先增大后减小 C、一直不变 D、先增大后不变

查看试题解析
9. 将进货单价为30元的某种商品按零售价100元1件卖出时，每天能卖出20件．若这种商品的零售价在一定范围内每降价1元，其日销售量就增加1件，为了获得最大的利润，则应降价（）

A、5元 B、15元 C、25元 D、35元

查看试题解析
10. 如图，在 $R t △ A B C$ 中， $∠ C = 90 °$ ， $B C = \sqrt{5}$ ，点D是AC上一点，连接BD.若 $t a n ∠ A = \frac{1}{2}$ ， $t a n ∠ A B D = \frac{1}{3}$ ，则CD的长为（）

A、 $2 \sqrt{5}$ B、3 C、 $\sqrt{5}$ D、2

查看试题解析

二、填空题

11. 若 $\frac{a}{b} = \frac{3}{2}$ ，则 $\frac{a + b}{b}$ ＝.

查看试题解析
12. 若三角形三个内角的比为1：2：3，则它的最长边与最短边的比为

查看试题解析
13. 如图， $Δ A B C$ 的顶点都在正方形网格纸的格点上，则 $s i n C =$ ．

查看试题解析
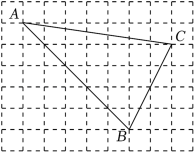14. 我国魏晋时期的数学家赵爽在为天文学著作《周髀算经》作注解时，用4个全等的直角三角形和中间的小正方形拼成一个大正方形，这个图被称为“弦图”．它体现了中国古代数学的成就．如图，已知大正方形 $A B C D$ 的面积是100，小正方形 $E F G H$ 的面积是4．则：（1） $A F =$ ；（2） $t a n ∠ A D F =$ ．

查看试题解析

三、解答题

15. 计算： $2 \tan 45 ° - \frac{1}{\sin 30 °} - 2 \sin^{2} 60 °$ .

查看试题解析
16. 如图，AD是△ABC中BC边上的高，且∠B=30°，∠C=45°，CD=2．求BC的长．

查看试题解析
17. 如图，在平面直角坐标系中， $△ A B C$ 的三个顶点坐标分别为 $A (1 ， - 3)$ ， $B (- 2 ， - 3)$ ， $C (2 ， - 1)$ ．

(1)、画出 $△ A B C$ 关于x轴对称的 $△ A_{1} B_{1} C_{1}$ ，点 $C_{1}$ 的坐标为 ▲ ；

(2)、以原点O为位似中心，在x轴上方画出 $△ A B C$ 放大2倍后的 $△ A_{2} B_{2} C_{2}$ ，点 $C_{2}$ 的坐标为 ▲ ．

查看试题解析
18. 如图，上午9时，一条船从A处出发，以每小时40海里的速度向正东方向航行，9时30分到达B处，从A，B两处分别测得小岛C在北偏东45°和北偏东15°．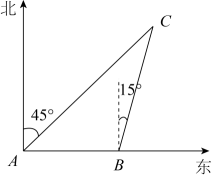

(1)、求∠C的度数；

(2)、求B处船与小岛C的距离（结果保留根号）．

查看试题解析
19. 如图，在平面直角坐标系xOy中， $△ A B C$ 是等腰直角三角形， $∠ B A C = 90 °$ ， $A (1 ， 0)$ ， $B (0 ， 2)$ ，抛物线 $y = \frac{1}{2} x^{2} + b x - 2$ 过点C．求抛物线的表达式．

查看试题解析
20. 如图，已知∠ABC和射线BD上一点P(点P与点B不重合)，且点P到BA、BC的距离为PE、PF．

(1)、若∠EBP＝40°，∠FBP＝20°，PB＝m，试比较PE、PF的大小；

(2)、若∠EBP＝α，∠FBP＝β，α，β都是锐角，且α＞β．试判断PE、PF的大小，并给出证明．

查看试题解析
21. 在2022年北京冬奥会上，为了得出一名滑雪运动员从山坡滑下时滑行距离 $s$ （单位： $m$ ）与滑行时间 $t$ （单位： $s$ ）之间的函数关系式，测得一组相关数据如下表．
滑行时间 $t / s$
0
1
2
3
4
滑行距离 $s / m$
0
4.5
14
28.5
48

(1)、以 $t$ 为横坐标， $s$ 为纵坐标建立平面直角坐标系（如图所示）．请描出表中数据对应的5个点，并用平滑的曲线连接它们；

(2)、观察图象，请你选用恰当的函数模型近似地表示 $s$ 与 $t$ 之间的函数关系，并求出这个函数关系式；

(3)、如果该滑雪运动员滑行了 $1040 m$ ，请你用（2）中的函数模型推算他滑行的时间．（参考数据： $10 2^{2} = 10404$ ）

查看试题解析
22. 如图，在平面直角坐标系xOy中，一次函数 $y = - x + 5$ 的图象与反比例函数 $y = \frac{k}{x} (k > 0)$ 的图象相交于A，B两点，与x轴相交于点C，连接OB，且 $△ B O C$ 的面积为 $\frac{5}{2}$ ．

(1)、求反比例函数的表达式；

(2)、将直线AB向下平移，若平移后的直线与反比例函数的图象只有一个交点，试说明直线AB向下平移了几个单位长度？

查看试题解析
23. 在四边形 $A B C D$ 中， $∠ A D C = ∠ A C B$ ， $A C$ 为对角线， $A D \cdot C B = D C \cdot A C$ ．

(1)、如图1，求证： $A C$ 平分 $∠ D A B$ ；

(2)、如图1，求 $A C = 8$ ， $A B = 12$ ，求 $A D$ 的长；

(3)、如图2，若 $∠ A D C = ∠ A C B = 90 °$ ， E为 $A B$ 的中点，连接 $C E$ 、 $D E$ ， $D E$ 与 $A C$ 交于点F， $C B = 6$ ， $C E = 5$ ，求 $\frac{D F}{E F}$ 的值．

查看试题解析

滑行时间 $t / s$	0	1	2	3	4
滑行距离 $s / m$	0	4.5	14	28.5	48