山西省临汾市2022-2023学年七年级上学期月考数学试卷（12月份）

试卷更新日期：2022-12-30 类型：月考试卷

进入出卷网下载

一、单选题

1. 数 $1 ， 0 ， - \frac{1}{2} ， - 3$ 中最大的是（）

A、1 B、-3 C、 $- \frac{1}{2}$ D、0

查看试题解析
2. 下列说法错误的是（）

A、没有最大的有理数 B、没有最小的有理数 C、有最小的正有理数 D、有绝对值最小的有理数

查看试题解析
3. 如图，房间地面的图案是用大小相同的黑、白正方形镶嵌而成．图中，第1个黑色形由3个正方形组成，第2个黑色形由7个正方形组成，那么组成第12个黑色形的正方形个数是（）

A、44 B、45 C、46 D、47

查看试题解析
4. 下列结论中，正确的是（）

A、若 $a b > 0$ ，则 $a > 0 ， b > 0$ B、若 $a b < 0$ ，则 $a < 0 ， b < 0$ C、若 $a b = 0$ ，则 $a = 0$ 且 $b = 0$ D、若 $a b > 0$ ，则 $a ， b$ 同号

查看试题解析
5. 如果 $\frac{1}{3}$ +=0，则“”表示的数应是（）

A、-3 B、3 C、 $\frac{1}{3}$ D、 $- \frac{1}{3}$

查看试题解析
6. 若 $x < 0$ 且 $| x | < 1$ ，则 $| \frac{| x - 1 |}{| x | + 1} |$ 的值（）

A、1 B、小于0 C、-1 D、大于0

查看试题解析
7. 质检员抽查4个足球，其中超过标准质量的克数记为正数，不足标准质量的克数记为负数，从轻重的角度看，最接近标准质量的足球是（）

A、 B、 C、 D、

查看试题解析
8. 在简便运算时，把 $24 \times (- 99 \frac{47}{48})$ 变形成最合适的形式是（）

A、 $24 \times (- 100 + \frac{1}{48})$ B、 $24 \times (- 100 - \frac{1}{48})$ C、 $24 \times (- 99 - \frac{47}{48})$ D、 $24 \times (- 99 + \frac{47}{48})$

查看试题解析
9. 下列运算正确的是（）

A、 $- 2 + (- 7) = - (7 - 2) = - 5$ B、 $(+ 3) + (- 8) = - (8 - 3) = - 5$ C、 $(- 9) - (- 2) = - (9 + 2) = - 11$ D、 $(+ 6) + (- 4) = + (6 + 4) = + 10$

查看试题解析
10. 如下图，数轴上一动点A向左移动2个单位长度到达点B，再向右移动5个单位度到达点C，若点C表示的数为1，则点A表示的数为（）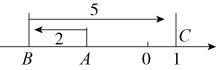

A、-1 B、+1 C、-2 D、-3

查看试题解析

二、填空题

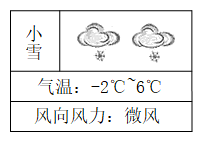
11. 小红和小花在玩一种计算的游戏，计算的规则是 $| \begin{array}{l} a b \\ c d \end{array} | = a d - b c$ ，现在轮到小红计算 $| \begin{array}{l} 1 - 1 \\ 2 8 \end{array} |$ 的值，请你帮忙算一算，结果是．

查看试题解析
12. 已知a，b互为相反数，c、d互为倒数，则 $2 (a + b) - 3 (- c d)^{100}$ 的值是．

查看试题解析
13. 某城市一月份日平均温度大约是零下4.5℃，用负数表示这个温度为℃．

查看试题解析
14. 用科学记数法表示13050000，应记作．

查看试题解析
15. 据中央台昨天报道，我国北方某城市天气情况如下图所示，则这个城市当天的温差是：℃．

查看试题解析

三、解答题

16. 西安市出租车公司司机小李某天下午的营运全是在南北走向的长安路上进行的，如果规定向南为正，向北为负，他这天下午行程如下（单位：km）
15，-2，5，-1，-10，-3，-2，12，4，-5，6

(1)、将最后一名乘客送到目的地时，小李距出发点多远？在出发点的南边还是北边？

(2)、若汽车耗气量为0.4L/km，这天下午小李开车共耗气多少升？

查看试题解析
17. 计算：

(1)、 $0.35 + (- 0.6) + 0.25 + (- 5.4)$

(2)、 $- 2.5 \div \frac{5}{16} \times (- \frac{1}{8}) \div (- 4)$ ；

(3)、 $(\frac{1}{6} - \frac{2}{3} + \frac{5}{12}) \div (- \frac{1}{36})$

(4)、 $- 1^{4} \times | 1 - \frac{7}{6} | + \frac{3}{4} \times [{(- \frac{2}{3})}^{2} - 2]$ ．

查看试题解析
18. 如图，数轴上A、B两点对应的有理数分别为20和30，点P和点Q分别同时从点A和点O出发，以每秒2个单位长度，每秒4个单位长度的速度向数轴正方向运动，设运动时间为t秒．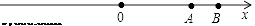

(1)、当t=2时，则P、Q两点对应的有理数分别是；PQ=；

(2)、点C是数轴上点B左侧一点，其对应的数是x，且CB=2CA，求x的值；

(3)、在点P和点Q出发的同时，点R以每秒8个单位长度的速度从点B出发，开始向左运动，遇到点Q后立即返回向右运动，遇到点P后立即返回向左运动，与点Q相遇后再立即返回，如此往返，直到P、Q两点相遇时，点R停止运动，求点R运动的路程一共是多少个单位长度？点R停止的位置所对应的数是多少？

查看试题解析
19. （阅读理解）数轴是一个非常重要的数学工具，它使数和数轴上的点建立起对应关系，揭示了数与点之间的内在联系，它是“数形结合”的基础．
例如：从“形”的角度看： $| 3 - 1 |$ 表示3与1差的绝对值，也可理解为数轴上表示3和1的两点之间的距离： $| 3 + 1 |$ 可以看做 $| 3 - (- 1) |$ ，表示3与-1的差的绝对值，也可理解为数轴上表示3与-1的两点之间的距离．
从“数”的角度看：数轴上表示4和-3的两点之间的距离可用代数式表示为： $| 4 - (- 3) |$ ．
根据以上阅读材料探索下列问题：

(1)、数轴上表示3和8的两点之间的距离是；数轴上表示3和-3的两点之间的距离是；

(2)、①若数轴上表示的数 $x$ 和-2的两点之间的距离是3，求 $x$ 的值；
②若数轴上某动点表示的数为 $x$ ，当式子 $| x - 1 | + | x + 2 |$ 取得最小值时，求相应整数 $x$ 的值．

查看试题解析
20. 粮库三天内发生粮食进出库的吨数如下：+26，-32，-15，+34，-38，-20．（其中“+”表示进库，“-”表示出库）

(1)、经过这三天，库里的粮食是增多（或是减少）了多少？

(2)、经过这三天，仓库管理员结算发现库里还存粮480吨，那么三天前库里存粮多少吨？

(3)、如果进出的装卸费都是每吨5元，那么这三天要付多少装卸费？

查看试题解析
21. 设a，b在数轴上表示的实数到原点的距离相等，且位于原点的两侧，c，d互为倒数，e的绝对值为1，请求出下列代数式的值：2a+2b- $\frac{c d}{3}$ +e．

查看试题解析
22. 有理数a、b、c在数轴上的位置如图所示，

(1)、判断a-b0，a-c0，b-c0；

(2)、化简|a-b|＋|a-c|-|b-c|．

查看试题解析
23. 计算：

(1)、 $- 2 \times (- \frac{1}{2})^{2} + | - 2 |^{3} - (- \frac{1}{2})$

(2)、 $- 1^{4} - (0.5 - \frac{2}{3}) \times [- 2 - (- 3)^{3}]$

(3)、 $4 x - 3 (20 - x) = 5 x - 7 (20 - x)$

(4)、 $1 - \frac{2 x - 5}{6} = \frac{3 - x}{4}$

查看试题解析
24. 足球的球面由若干个五边形和正六边形拼接而成，已知有12块正五边形，则正六边形的块数是？

查看试题解析