山西省吕梁市临县2022—2023学年八年级上学期数学期末测试题
试卷更新日期:2022-12-30 类型:期末考试
一、单选题
-
1. 下列长度的三条线段,能构成三角形的是( )A、3 ,10 ,5 B、4 ,8 ,4 C、5 ,13 ,12 D、2 ,7 ,42. 下列各组图形中,是全等形的是( )A、两个含30°角的直角三角形 B、一个钝角相等的两个等腰三角形 C、边长为5和6的两个等腰三角形 D、腰对应相等的两个等腰直角三角形3. 已知:在△ABC中,∠A=60°,如要判定△ABC是等边三角形,还需添加一个条件.现有下面三种说法:
①如果添加条件“AB=AC”,那么△ABC是等边三角形;
②如果添加条件“∠B=∠C”,那么△ABC是等边三角形;
③如果添加条件“边AB、BC上的高相等”,那么△ABC是等边三角形.
上述说法中,正确的有( )
A、3个 B、2个 C、1个 D、0个4. 计算 的结果为( )A、-4x6 B、-4x7 C、4x8 D、-4x85. 图(1)是一个长为2a,宽为的长方形,用剪刀沿图中虚线(对称轴)剪开,把它分成四块形状和大小完全相同的小长方形,然后按图(2)那样拼成一个正方形,则中间空余的部分的面积是( )
 A、ab B、 C、 D、6. 化简 的结果是( )A、 +1 B、 C、 D、7. 在△ABC中,∠B=∠C,与△ABC全等的三角形有一个角是100° , 那么△ABC中与这个角对应的角是( )A、∠A B、∠B C、∠C D、∠D8. 如图,是等边三角形, , 于点,于点, , 则四个结论:①点在的平分线上;②;③;④≌ , 正确的结论是( ).
A、ab B、 C、 D、6. 化简 的结果是( )A、 +1 B、 C、 D、7. 在△ABC中,∠B=∠C,与△ABC全等的三角形有一个角是100° , 那么△ABC中与这个角对应的角是( )A、∠A B、∠B C、∠C D、∠D8. 如图,是等边三角形, , 于点,于点, , 则四个结论:①点在的平分线上;②;③;④≌ , 正确的结论是( ). A、①②③④ B、①② C、只有②③ D、只有①③9. 已知x2+2(m-1)x+9是一个完全平方式,则m的值为( )A、4 B、4或-2 C、±4 D、-210. 对于非零实数 ,规定 ,若 ,则 的值为( )A、 B、 C、 D、
A、①②③④ B、①② C、只有②③ D、只有①③9. 已知x2+2(m-1)x+9是一个完全平方式,则m的值为( )A、4 B、4或-2 C、±4 D、-210. 对于非零实数 ,规定 ,若 ,则 的值为( )A、 B、 C、 D、二、填空题
-
11. 如图所示,三角形ABC的面积为1cm2 . AP垂直∠B的平分线BP于点P.则三角形PBC的面积是
 12. 因式分解:x3﹣4x= .
12. 因式分解:x3﹣4x= .
13. 如果关于x的分式方程无解,则m的值为14. 如图, , 若 , 则的度数为 .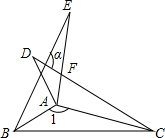 15. 如图,点B在射线AN上,以为边作等边 , M为中点,且 , P为中点,当最小时, .
15. 如图,点B在射线AN上,以为边作等边 , M为中点,且 , P为中点,当最小时, .
三、解答题
-
16. 先化简,再求值: ,其中x是从﹣2,﹣1,1,2中选取的一个合适的数.17. 在△ABC中,BC=8,AB=1;(1)、若AC是整数,求AC的长;(2)、已知BD是△ABC的中线,若△ABD的周长为10,求△BCD的周长.18. 已知:如图,在四边形中, , 点是的中点.
 (1)、求证:是等腰三角形:(2)、当°时,是等边三角形.19. 从边长为 a 的正方形剪掉一个边长为 b 的正方形(如图 1),然后将剩余部分拼成一个长方形(如图 2).
(1)、求证:是等腰三角形:(2)、当°时,是等边三角形.19. 从边长为 a 的正方形剪掉一个边长为 b 的正方形(如图 1),然后将剩余部分拼成一个长方形(如图 2).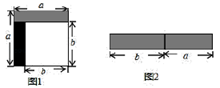 (1)、上述操作能验证的等式是 (请选择正确的一个)A、a ﹣2ab+b =(a﹣b) B、a ﹣b =(a+b)(a﹣b) C、a +ab=a(a+b)(2)、若 x ﹣9y =12,x+3y=4,求 x﹣3y 的值;(3)、计算: .20. 若我们规定三角“
(1)、上述操作能验证的等式是 (请选择正确的一个)A、a ﹣2ab+b =(a﹣b) B、a ﹣b =(a+b)(a﹣b) C、a +ab=a(a+b)(2)、若 x ﹣9y =12,x+3y=4,求 x﹣3y 的值;(3)、计算: .20. 若我们规定三角“ ”表示为:abc;方框“
”表示为:abc;方框“ ”表示为: . 例如:
”表示为: . 例如: . 请根据这个规定解答下列问题: (1)、计算:
. 请根据这个规定解答下列问题: (1)、计算: =; (2)、代数式
=; (2)、代数式 为完全平方式,则k=; (3)、解方程:
为完全平方式,则k=; (3)、解方程: . 21. 某商场计划购进一批甲、乙两种玩具,已知一件甲种玩具的进价与一件乙种玩具的进价的和为40元,用90元购进甲种玩具的件数与用150元购进乙种玩具的件数相同.(1)、求每件甲种、乙种玩具的进价分别是多少元?(2)、商场计划购进甲、乙两种玩具共48件,其中甲种玩具的件数少于乙种玩具的件数,商场决定此次进货的总资金不超过1000元,求商场共有几种进货方案?22. 如图
. 21. 某商场计划购进一批甲、乙两种玩具,已知一件甲种玩具的进价与一件乙种玩具的进价的和为40元,用90元购进甲种玩具的件数与用150元购进乙种玩具的件数相同.(1)、求每件甲种、乙种玩具的进价分别是多少元?(2)、商场计划购进甲、乙两种玩具共48件,其中甲种玩具的件数少于乙种玩具的件数,商场决定此次进货的总资金不超过1000元,求商场共有几种进货方案?22. 如图 (1)、已知 , , O为中点,过O点的直线分别与相交于点M,N,如图1,那么与有什么关系?请说明理由.(2)、若将过O点的直线旋转至图2、3的情况时,其它条件不变,那么图1中的与的关系还成立吗?请说明理由.23. 如图
(1)、已知 , , O为中点,过O点的直线分别与相交于点M,N,如图1,那么与有什么关系?请说明理由.(2)、若将过O点的直线旋转至图2、3的情况时,其它条件不变,那么图1中的与的关系还成立吗?请说明理由.23. 如图 (1)、如图①,在四边形中, , , , 分别是边 , 上的点,且 . 请直接写出线段 , , 之间的数量关系:;(2)、如图②,在四边形中, , , , 分别是边 , 上的点,且 , (1)中的结论是否仍然成立?请写出证明过程;(3)、在四边形中, , , , 分别是边 , 所在直线上的点,且 . 请画出图形(除图②外),并直接写出线段 , , 之间的数量关系.
(1)、如图①,在四边形中, , , , 分别是边 , 上的点,且 . 请直接写出线段 , , 之间的数量关系:;(2)、如图②,在四边形中, , , , 分别是边 , 上的点,且 , (1)中的结论是否仍然成立?请写出证明过程;(3)、在四边形中, , , , 分别是边 , 所在直线上的点,且 . 请画出图形(除图②外),并直接写出线段 , , 之间的数量关系.