2022年全国中考数学真题分类汇编25 数据统计与分析
试卷更新日期：2022-12-29 类型：二轮复习
一、单选题
-
1. 为深入落实“立德树人”的根本任务，坚持德、智、体、美、劳全面发展，某学校积极推进学生综合素质评价改革，某同学在本学期德智体美劳的评价得分如图所示，则该同学五项评价得分的众数，中位数，平均数分别为（ ）
A、8，8，8 B、7，7，7.8 C、8，8，8.6 D、8，8，8.42. 某公司对25名营销人员4月份销售某种商品的情况统计如下：销售量（件）
60
50
40
35
30
20
人数
1
4
4
6
7
3
则这25名营销人员销售量的众数是（ ）
A、50 B、40 C、35 D、303. 如图是某品牌运动服的S号，M号，L号，XL号的销售情况统计图，则厂家应生产最多的型号为（ ）
A、S号 B、M号 C、L号 D、XL号4. 在一次中学生运动会上，参加男子跳高的8名运动员的成绩分别为（单位：m）：1.75 1.80 1.75 1.70 1.70 1.65 1.75 1.60本组数据的众数是（ ）A、1.65 B、1.70 C、1.75 D、1.805. 若一组数据1，2，4，3， ， 0的平均数是2，则众数是（ ）A、1 B、2 C、3 D、46. 我国近十年的人口出生率及人口死亡率如图所示．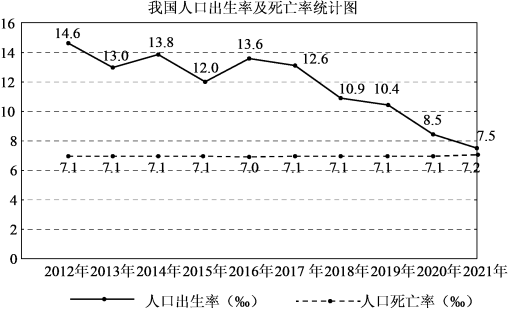
已知人口自然增长率=人口出生率—人口死亡率，下列判断错误的是（ ）
A、与2012年相比，2021年的人口出生率下降了近一半 B、近十年的人口死亡率基本稳定 C、近五年的人口总数持续下降 D、近五年的人口自然增长率持续下降7. 某学习小组做摸球试验，在一个不透明的袋子里装有红、黄两种颜色的小球共20个，除颜色外都相同．将球搅匀后，随机摸出5个球，发现3个是红球，估计袋中红球的个数是（ ）A、12 B、9 C、8 D、68. 我市某校开展共创文明班，一起向未来的古诗文朗诵比赛活动，有10位同学参加了初赛，按初赛成绩由高到低取前5位进入决赛．如果小王同学知道了自己的成绩后，要判断能否进入决赛，他需要知道这10位同学成绩的（ ）A、平均数 B、众数 C、中位数 D、方差9. 一组数据-2，0，3，1，-1的极差是（ ）A、2 B、3 C、4 D、510. 已知一组数据：111，113，115，115，116，这组数据的平均数和众数分别是（ ）A、114，115 B、114，114 C、115，114 D、115，11511. 为迎接党的二十大胜利召开，某校开展了“学党史，悟初心”系列活动.学校对学生参加各项活动的人数进行了调查，并将数据绘制成如下统计图.若参加“书法”的人数为80人，则参加“大合唱”的人数为（ ）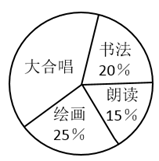
A、60人 B、100人 C、160人 D、400人12. 在体育测试中，7名女生仰卧起坐的成绩如下（次/分钟）：38，42，42，45，43，45，45，则这组数据的众数是（ ）A、38 B、42 C、43 D、45二、填空题
-
13. 一组数据3、-2、4、1、4的平均数是.14. 某班40名学生体重的频数分布直方图（不完整）如图所示，组距为 ．
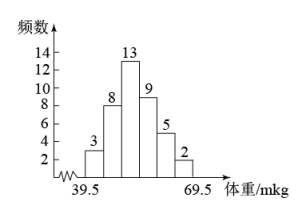15. 为了了解“双减”背景下全国中小学生完成课后作业的时间情况，比较适合的调查方式是（填“全面调查”或“抽样调查”）．16. 学校要从王静，李玉两同学中选拔一人参加运动会志愿者工作，选拔项目为普通话，体育知识和旅游知识.并将成绩依次按4∶3∶3计分. 两人的各项选拔成绩如右表所示，则最终胜出的同学是.普通话
体育知识
旅游知识
王静
80
90
70
李玉
90
80
70
17. 某射击运动队进行了五次射击测试，甲、乙两名选手的测试成绩如图所示，甲、乙两选手成绩的方差分别记为 ， 则.（填“>”“<”或“=”）
18. 已知一组数据：4，5，5，6，5，4，7，8，则这组数据的众数是.三、综合题
-
19. 某校计划成立学生体育社团，为了解学生对不同体育项目的喜爱情况，学校随机抽取了部分学生进行“我最喜爱的一个体育项目”问卷调查，规定每人必须并且只能在“篮球”“足球”“乒乓球”“健美操”“跑步”五个项目中选择一项，并根据统计结果绘制了两幅不完整的统计图.
请解答下列问题：
(1)、在这次调查中，该校一共抽样调查了名学生，扇形统计图中“跑步”项目所对应的扇形圆心角的度数是°；(2)、请补全条形统计图；(3)、若该校共有1200名学生，试估计该校学生中最喜爱“篮球”项目的人数.20. 为提高学生阅读兴趣，培养良好阅读习惯，2021年3月31日，教育部印发了《中小学生课外读物进校园管理办法》的通知.某学校根据通知精神，积极优化校园阅读环境，推动书香校园建设，开展了“爱读书、读好书、善读书”主题活动，随机抽取部分学生同时进行“你最喜欢的课外读物”（只能选一项）和“你每周课外阅读的时间”两项问卷调查，并绘制成如图1，图2的统计图.图1中A代表“喜欢人文类”的人数，B代表“喜欢社会类”的人数，C代表“喜欢科学类”的人数，D代表“喜欢艺术类”的人数.已知A为56人，且对应扇形圆心角的度数为126°.请你根据以上信息解答下列问题：
(1)、在扇形统计图中，求出“喜欢科学类”的人数；(2)、补全条形统计图；(3)、该校共有学生3200人，估计每周课外阅读时间不低于3小时的人数.21. 【新知学习】在气象学上，“入夏”由两种平均气温与22℃比较来判断：衢州市2021年5月5日~5月14日的两种平均气温统计表 （单位：℃）
注：“五天滑动平均气温”指某一天及其前后各两天的日平均气温的平均数，如：
(℃)．
已知2021年的从5月8日起首次连续五天大于或等于22℃，而对应着~ ， 其中第一个大于或等于22℃的是 ， 则5月7日即为我市2021年的“入夏日”．
【新知应用】已知我市2022年的“入夏日”为下图中的某一天，请根据信息解决问题：
衢州市2022年5月24日~6月2日的两种平均气温折线统计图
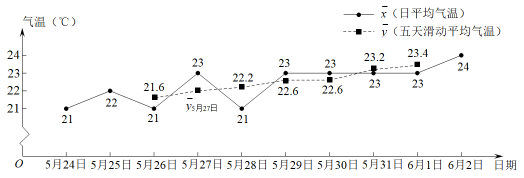(1)、求2022年的.(2)、写出从哪天开始，图中的连续五天都大于或等于22℃．并判断今年的“入夏日”．(3)、某媒体报道：“夏天姗姗来迟，衢州2022年的春天比去年长．”你认为这样的说法正确吗？为什么？（我市2021年和2022年的入春时间分别是2月1日和2月27日）22. 教育部在《大中小学劳动教育指导纲要（试行）》中明确要求：初中生每周课外生活和家庭生活中，劳动时间不少于3小时．某走读制初级中学为了解学生劳动时间的情况，对学生进行了随机抽样调查，并将调查结果制成不完整的统计图表，如图：平均每周劳动时间的频数统计表
劳动时间小时
频数
t＜3
9
3≤t＜4
a
4≤t＜5
66
t≥5
15
请根据图表信息，回答下列问题．
(1)、参加此次调查的总人数是人，频数统计表中a＝；(2)、在扇形统计图中，D组所在扇形的圆心角度数是°；(3)、该校准备开展以“劳动美”为主题的教育活动，要从报名的2男2女中随机挑选2人在活动中分享劳动心得，请用树状图或列表法求恰好抽到一名男生和一名女生的概率．23. 为扎实推进“五育并举”工作，某校利用课外活动时间开设了舞蹈、篮球、围棋和足球四个社团活动，每个学生只选择一项活动参加．为了解活动开展情况，学校随机抽取部分学生进行调查，将调查结果绘成如下表格和扇形统计图．参加四个社团活动人数统计表
社团活动
舞蹈
篮球
围棋
足球
人数
50
30
80
参加四个社团活动人数扇形统计图
请根据以上信息，回答下列问题：
(1)、抽取的学生共有人，其中参加围棋社的有人；(2)、若该校有3200人，估计全校参加篮球社的学生有多少人？(3)、某班有3男2女共5名学生参加足球社，现从中随机抽取2名学生参加学校足球队，请用树状图或列表法说明恰好抽到一男一女的概率．24. 某地交警在一个路口对某个时段来往的车辆的车速进行监测，统计数据如下表：车速（）
40
41
42
43
44
45
频数
6
8
15
3
2
其中车速为40、43（单位：）的车辆数分别占监测的车辆总数的12%、32%．
(1)、求出表格中的值；(2)、如果一辆汽车行驶的车速不超过的10%，就认定这辆车是安全行驶．若一年内在该时段通过此路口的车辆有20000辆，试估计其中安全行驶的车辆数．25. 某中学为了解学生每学期诵读经典的情况，在全校范围内随机抽查了部分学生上一学期阅读量，学校将阅读量分成优秀、良好、较好、一般四个等级，绘制如下统计表：等级
一般
较好
良好
优秀
阅读量/本
3
4
5
6
频数
12
a
14
4
频率
0.24
0.40
b
c
请根据统计表中提供的信息，解答下列问题：
(1)、本次调查一共随机抽取了名学生；表中 ， ， ．(2)、求所抽查学生阅读量的众数和平均数．(3)、样本数据中优秀等级学生有4人，其中仅有1名男生．现从中任选派2名学生去参加读书分享会，请用树状图法或列表法求所选2名同学中有男生的概率26. 在“双减”背景下，某区教育部门想了解该区A，B两所学校九年级各500名学生的课后书面作业时长情况，从这两所学校分别随机抽取50名九年级学生的课后书面作业时长数据（保留整数），整理分析过程如下：【收集数据】A学校50名九年级学生中，课后书面作业时长在70.5≤x＜80.5组的具体数据如下：
74，72，72，73，74，75，75，75，75，
75，75，76，76，76，77，77，78，80
【整理数据】不完整的两所学校的频数分布表如下，不完整的A学校频数分布直方图如图所示：
组别
50.5≤x＜60.5
60.5≤x＜70.5
70.5≤x＜80.5
80.5≤x＜90.5
90.5≤x＜100.5
A学校
5
15
x
8
4
B学校
7
10
12
17
4
【分析数据】两组数据的平均数、众数、中位数、方差如下表：特征数
平均数
众数
中位数
方差
A学校
74
75
y
127.36
B学校
74
85
73
144.12
根据以上信息，回答下列问题：
(1)、本次调查是调查（选填“抽样”或“全面”）；(2)、统计表中，x＝ ， y＝；(3)、补全频数分布直方图；(4)、在这次调查中，课后书面作业时长波动较小的是学校（选填“A”或“B”）；(5)、按规定，九年级学生每天课后书面作业时长不得超过90分钟，估计两所学校1000名学生中，能在90分钟内（包括90分钟）完成当日课后书面作业的学生共有人．27. 宁夏某枸杞育种改良试验基地对新培育的甲、乙两个品种各试种一亩，从两块试验地中各随机抽取10棵，对其产量（千克/棵）进行整理分析．下面给出了部分信息：甲品种：2.0，3.2，3.1，3.2，3.1，2.5，3.2，3.6，3.8，3.9
乙品种：如图所示
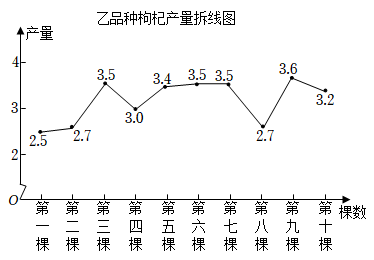
平均数
中位数
众数
方差
甲品种
3.16
3.2
0.29
乙品种
3.16
3.3
0.15
根据以上信息，完成下列问题：(1)、填空： ， ；(2)、若乙品种种植棵，估计其产量不低于千克的棵数；(3)、请从某一个方面简要说明哪个品种更好．28. 某学校为满足学生多样化学习需求，准备组建美术、劳动、科普、阅读四类社团．学校为了解学生的参与度，随机抽取了部分学生进行调查，将调查结果绘制成如图所示的不完整的统计图．请根据图中的信息，解答下列问题：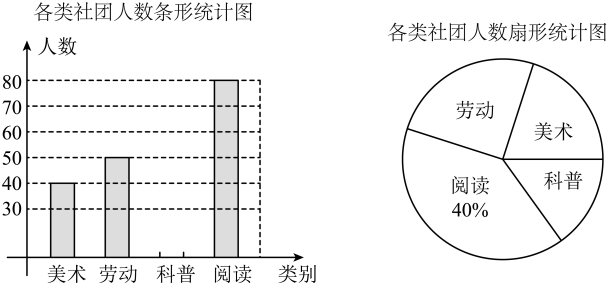
(1)、求本次调查的学生人数，并补全条形统计图；(2)、若全校共有学生3600人，求愿意参加劳动类社团的学生人数；(3)、甲、乙两名同学决定在阅读、美术、劳动社团中选择参加一种社团，请用树状图或列表法表示出所有等可能结果，并求出恰好选中同一社团的概率．29. 为了了解八年级学生本学期参加社会实践活动的天数情况，A，B两个县区分别随机抽查了200名八年级学生．根据调查结果绘制了统计图表，部分图表如下：
A，B两个县区的统计表
平均数
众数
中位数
A县区
3.85
3
3
B县区
3.85
4
2.5
(1)、若A县区八年级共有约5000名学生，估计该县区八年级学生参加社会实践活动不少于3天的学生约为名；(2)、请对A，B两个县区八年级学生参加社会实践活动的天数情况进行比较，做出判断，并说明理由．30. 合理的膳食可以保证青少年体格和智力的正常发育．综合实践小组为了解某校学生膳食营养状况，从该校1380名学生中调查了100名学生的膳食情况，调查数据整理如下：
中国营养学会推荐的三大营养素供能比参考值
蛋白质
10%~15%
脂肪
20%~30%
碳水化合物
50%~65%
注：供能比为某物质提供的能量占人体所需总能量的百分比．
(1)、本次调查采用的调查方法；（填“普查”或“抽样调查”）(2)、通过对调查数据的计算，样本中的蛋白质平均供能比约为14.6%，请计算样本中的脂肪平均供能比和碳水化合物平均供能比；(3)、结合以上的调查和计算，对照下表中的参考值，请你针对该校学生膳食状况存在的问题提一条建议．31. 为减少传统塑料袋对生态环境的破坏，国家提倡使用可以在自然环境下（特定微生物、温度、湿度）较快完成降解的环保塑料袋.调查小组就某小区每户家庭1周内环保塑料袋的使用情况进行了抽样调查，使用情况为（不使用）、（1~3个）、（4~6个）、（7个及以上），以下是根据调查结果绘制的统计图的一部分.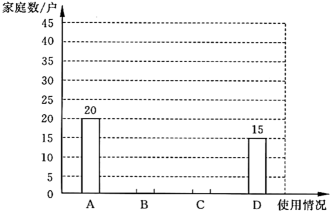
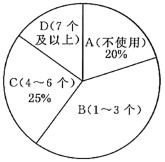(1)、本次调查的样本容量是 ， 请补全条形统计图；(2)、已知该小区有1500户家庭，调查小组估计：该小区1周内使用7个及以上环保塑料袋的家庭约有225户.调查小组的估计是否合理？请说明理由.32. 农业、工业和服务业统称为“三产”，2021年泰州市“三产”总值增长率在全省排名第一.观察下列两幅统计图，回答问题.
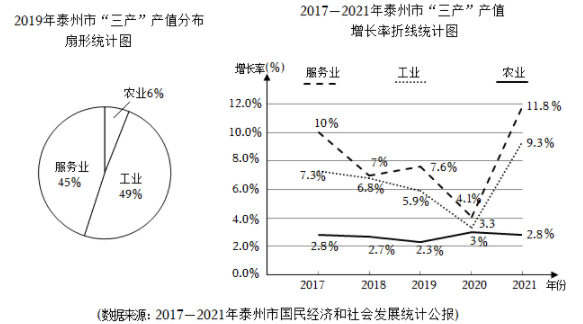(1)、2017—2021年农业产值增长率的中位数是%﹔若2019年“三产”总值为5200亿元，则2020年服务业产值比2019年约增加亿元（结果保留整数）.(2)、小亮观察折线统计图后认为：这五年中，每年服务业产值都比工业产值高，你同意他的说法吗?请结合扇形统计图说明你的理由.33. 育人中学初二年级共有200名学生，2021年秋学期学校组织初二年级学生参加30秒跳绳训练，开学初和学期末分别对初二年级全体学生进行了摸底测试和最终测试，两次测试数据如下：育人中学初二学生30秒跳绳测试成绩的频数分布表
跳绳个数（x）
x≤50
50＜x≤60
60＜x≤70
70＜x≤80
x＞80
频数（摸底测试）
19
27
72
a
17
频数（最终测试）
3
6
59
b
c
育人中学初二学生30秒跳绳最终测试成绩的扇形统计图
(1)、表格中a＝；(2)、请把下面的扇形统计图补充完整；（只需标注相应的数据）(3)、请问经过一个学期的训练，该校初二年级学生最终测试30秒跳绳超过80个的人数有多少？34. 某校九年级640名学生在“信息素养提升”培训前、后各参加了一次水平相同的测试，并以同一标准折算成“6分”、“7分”、“8分”、“9分”、“10分”5个成绩.为了解培训效果，用抽样调查的方式从中抽取了32名学生的2次测试成绩，并用划记法制成了如下表格：培训前
成绩（分）
6
7
8
9
10
划记
正正
正
正
人数（人）
12
4
7
5
4
培训后
成绩（分）
6
7
8
9
10
划记
一
正
正正正
人数（人）
4
1
3
9
15
(1)、这32名学生2次测试成绩中，培训前测试成绩的中位数是m，培训后测试成绩的中位数是n，则mn；（填“＞”、“＜”或“＝”）(2)、这32名学生经过培训，测试成绩为“6分”的百分比比培训前减少了多少？(3)、估计该校九年级640名学生经过培训，测试成绩为“10分”的学生增加了多少人？35. 为了解某校九年级学生开展“综合与实践”活动的情况，抽样调查了该校名九年级学生上学期参加“综合与实践”活动的天数，并根据调查所得的数据绘制了如下尚不完整的两幅统计图.根据图表信息，解答下列问题：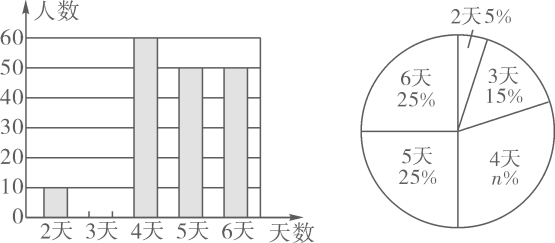
(1)、 ， ；(2)、补全条形统计图；(3)、根据抽样调查的结果，请你估计该校九年级2000名学生中上学期参加“综合与实践”活动4天及以上的人数.36. 某校初一年级有600名男生 ，为增强体质，拟在初一男生中开展引体向上达标测试活动.为制定合格标准，开展如下调查统计活动.(1)、A调查组从初一体育社团中随机抽取20名男生进行引体向上测试，B调查组从初一所有男生中随机抽取20名男生进行引体向上测试，其中（填“A”或“B”），调查组收集的测试成绩数据能较好地反映该校初一男生引体向上的水平状况；(2)、根据合理的调查方式收集到的测试成绩数据记录如下：成绩/个
2
3
4
5
7
13
14
15
人数/人
1
1
1
8
5
1
2
1
这组测试成绩的平均数为个，中位数为个；
(3)、若以（2）中测试成绩的中位数作为该校初一男生引体向上的合格标准，请估计该校初一有多少名男生不能达到合格标准.37. 为落实国家“双减”政策，某校为学生开展了课后服务，其中在体育类活动中开设了四种运动项目： 乒乓球， 排球， 篮球， 跳绳.为了解学生最喜欢哪一种运动项目，随机抽取部分学生进行调查（每位学生仅选一种），并将调查结果制成如下尚不完整的统计图表.问卷情况统计表
运动项目
人数
乒乓球
排球
10
篮球
80
跳绳
70
(1)、本次调查的样本容量是 ， 统计表中 ；(2)、在扇形统计图中，“ 排球”对应的圆心角的度数是 ；(3)、若该校共有2000名学生，请你估计该校最喜欢“ 乒乓球”的学生人数.