2022年全国中考数学真题分类汇编24 几何图形综合题
试卷更新日期:2022-12-29 类型:二轮复习
一、单选题
-
1. 如图,在中, , 将以点为中心逆时针旋转得到 , 点在边上,交于点.下列结论:①;②平分;③ , 其中所有正确结论的序号是( )
 A、①② B、②③ C、①③ D、①②③2. 如图,小明家仿古家具的一块三角形形状的玻璃坏了,需要重新配一块.小明通过电话给玻璃店老板提供相关数据,为了方便表述,将该三角形记为 , 提供了下列各组元素的数据,配出来的玻璃不一定符合要求的是( )
A、①② B、②③ C、①③ D、①②③2. 如图,小明家仿古家具的一块三角形形状的玻璃坏了,需要重新配一块.小明通过电话给玻璃店老板提供相关数据,为了方便表述,将该三角形记为 , 提供了下列各组元素的数据,配出来的玻璃不一定符合要求的是( ) A、 B、 C、 D、3. 若等腰三角形的两边长分别是3cm和5cm,则这个等腰三角形的周长是( )A、8cm B、13cm C、8cm或13cm D、11cm或13cm4. 如图,将矩形 沿着 、 、 翻折,使得点 、 、 恰好都落在点 处,且点 、 、 在同一条直线上,同时点 、 、 在另一条直线上.小炜同学得出以下结论:
A、 B、 C、 D、3. 若等腰三角形的两边长分别是3cm和5cm,则这个等腰三角形的周长是( )A、8cm B、13cm C、8cm或13cm D、11cm或13cm4. 如图,将矩形 沿着 、 、 翻折,使得点 、 、 恰好都落在点 处,且点 、 、 在同一条直线上,同时点 、 、 在另一条直线上.小炜同学得出以下结论:① ;② ;③ ;④ ;⑤ .
其中正确的是( )
 A、①②③ B、①③④ C、①④⑤ D、②③④
A、①②③ B、①③④ C、①④⑤ D、②③④二、填空题
-
5. 【阅读材料】如图①,四边形 中, , ,点 , 分别在 , 上,若 ,则 .

【解决问题】如图②,在某公园的同一水平面上,四条道路围成四边形 .已知 , , , ,道路 , 上分别有景点 , ,且 , ,若在 , 之间修一条直路,则路线 的长比路线 的长少 (结果取整数,参考数据: ).
 6. 如图,在矩形ABCD中 .动点M从点A出发,沿边AD向点D匀速运动,动点N从点B出发,沿边BC向点C匀速运动,连接MN.动点M,N同时出发,点M运动的速度为 ,点N运动的速度为 ,且 .当点N到达点C时,M,N两点同时停止运动.在运动过程中,将四边形MABN沿MN翻折,得到四边形 .若在某一时刻,点B的对应点 恰好在CD的中点重合,则 的值为.
6. 如图,在矩形ABCD中 .动点M从点A出发,沿边AD向点D匀速运动,动点N从点B出发,沿边BC向点C匀速运动,连接MN.动点M,N同时出发,点M运动的速度为 ,点N运动的速度为 ,且 .当点N到达点C时,M,N两点同时停止运动.在运动过程中,将四边形MABN沿MN翻折,得到四边形 .若在某一时刻,点B的对应点 恰好在CD的中点重合,则 的值为.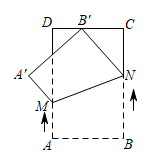 7. 如图,在平行四边形ABCD中, , , ,分别以A,C为圆心,大于 的长为半径画弧,两弧相交于点M,N,过M,N两点作直线,与BC交于点E,与AD交于点F,连接AE,CF,则四边形AECF的周长为.
7. 如图,在平行四边形ABCD中, , , ,分别以A,C为圆心,大于 的长为半径画弧,两弧相交于点M,N,过M,N两点作直线,与BC交于点E,与AD交于点F,连接AE,CF,则四边形AECF的周长为.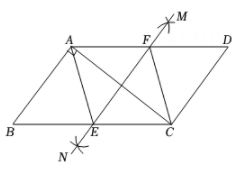 8. 定义:一个三角形的一边长是另一边长的2倍,这样的三角形叫做“倍长三角形”.若等腰△ABC是“倍长三角形”,底边BC的长为3,则腰AB的长为.9. “做数学”可以帮助我们积累数学活动经验.如图,已知三角形纸片 , 第1次折叠使点落在边上的点处,折痕交于点;第2次折叠使点落在点处,折痕交于点.若 , 则.
8. 定义:一个三角形的一边长是另一边长的2倍,这样的三角形叫做“倍长三角形”.若等腰△ABC是“倍长三角形”,底边BC的长为3,则腰AB的长为.9. “做数学”可以帮助我们积累数学活动经验.如图,已知三角形纸片 , 第1次折叠使点落在边上的点处,折痕交于点;第2次折叠使点落在点处,折痕交于点.若 , 则.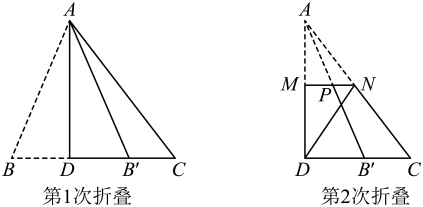 10. 在中, , 分别为的对边,若 , 则的值为.
10. 在中, , 分别为的对边,若 , 则的值为.三、综合题
-
11. 如图,二次函数的图象与x轴交于O(O为坐标原点),A两点,且二次函数的最小值为 , 点是其对称轴上一点,y轴上一点.
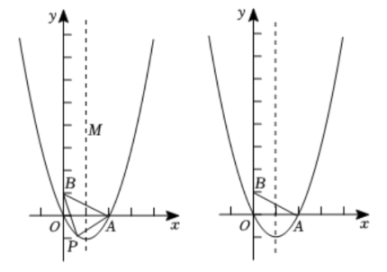 (1)、求二次函数的表达式;(2)、二次函数在第四象限的图象上有一点P,连结 , , 设点P的横坐标为t,的面积为S,求S与t的函数关系式;(3)、在二次函数图象上是否存在点N,使得以A、B、M、N为顶点的四边形是平行四边形?若存在,直接写出所有符合条件的点N的坐标,若不存在,请说明理由.12. 在平面直角坐标系中,抛物线L1:y=ax2+2x+b与x轴交于两点A,B(3,0),与y轴交于点C(0,3).
(1)、求二次函数的表达式;(2)、二次函数在第四象限的图象上有一点P,连结 , , 设点P的横坐标为t,的面积为S,求S与t的函数关系式;(3)、在二次函数图象上是否存在点N,使得以A、B、M、N为顶点的四边形是平行四边形?若存在,直接写出所有符合条件的点N的坐标,若不存在,请说明理由.12. 在平面直角坐标系中,抛物线L1:y=ax2+2x+b与x轴交于两点A,B(3,0),与y轴交于点C(0,3).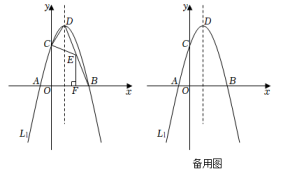 (1)、求抛物线L1的函数解析式,并直接写出顶点D的坐标;(2)、如图,连接BD,若点E在线段BD上运动(不与B,D重合),过点E作EF⊥x轴于点F,设EF=m,问:当m为何值时,△BFE与△DEC的面积之和最小;(3)、若将抛物线L1绕点B旋转180°得抛物线L2 , 其中C,D两点的对称点分别记作M,N.问:在抛物线L2的对称轴上是否存在点P,使得以B,M,P为顶点的三角形为等腰三角形?若存在,直接写出所有符合条件的点P的坐标;若不存在,请说明理由.13. 已知抛物线 与x轴相交于点 , ,与y轴相交于点C.
(1)、求抛物线L1的函数解析式,并直接写出顶点D的坐标;(2)、如图,连接BD,若点E在线段BD上运动(不与B,D重合),过点E作EF⊥x轴于点F,设EF=m,问:当m为何值时,△BFE与△DEC的面积之和最小;(3)、若将抛物线L1绕点B旋转180°得抛物线L2 , 其中C,D两点的对称点分别记作M,N.问:在抛物线L2的对称轴上是否存在点P,使得以B,M,P为顶点的三角形为等腰三角形?若存在,直接写出所有符合条件的点P的坐标;若不存在,请说明理由.13. 已知抛物线 与x轴相交于点 , ,与y轴相交于点C.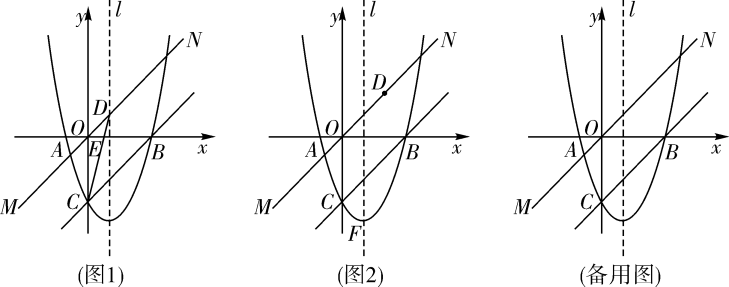 (1)、求抛物线的表达式;(2)、如图1,将直线BC间上平移,得到过原点O的直线MN.点D是直线MN上任意一点.
(1)、求抛物线的表达式;(2)、如图1,将直线BC间上平移,得到过原点O的直线MN.点D是直线MN上任意一点.①当点D在抛物线的对称轴l上时,连接CD,关x轴相交于点E,求线段OE的长;
②如图2,在抛物线的对称轴l上是否存在点F,使得以B,C,D,F为顶点的四边形是平行四边形?若存在,求出点F与点D的坐标;若不存在,请说明理由.
14. 如图,抛物线y=ax2+bx+c与x轴交于A(﹣4,0),B(2,0),与y轴交于点C(0,2).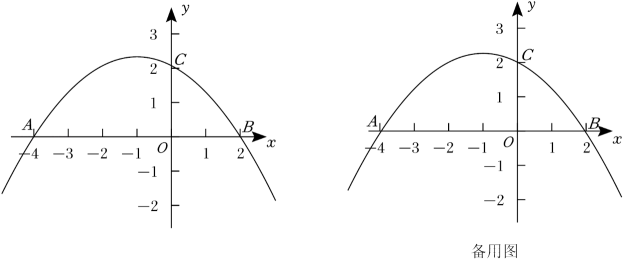 (1)、求这条抛物线所对应的函数的表达式;(2)、若点D为该抛物线上的一个动点,且在直线AC上方,求点D到直线AC的距离的最大值及此时点D的坐标;(3)、点P为抛物线上一点,连接CP,直线CP把四边形CBPA的面积分为1:5两部分,求点P的坐标.15. 已知抛物线经过A(-1,0)、B(0、3)、 C(3,0)三点,O为坐标原点,抛物线交正方形OBDC的边BD于点E,点M为射线BD上一动点,连接OM ,交BC于点F
(1)、求这条抛物线所对应的函数的表达式;(2)、若点D为该抛物线上的一个动点,且在直线AC上方,求点D到直线AC的距离的最大值及此时点D的坐标;(3)、点P为抛物线上一点,连接CP,直线CP把四边形CBPA的面积分为1:5两部分,求点P的坐标.15. 已知抛物线经过A(-1,0)、B(0、3)、 C(3,0)三点,O为坐标原点,抛物线交正方形OBDC的边BD于点E,点M为射线BD上一动点,连接OM ,交BC于点F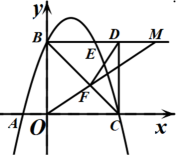 (1)、求抛物线的表达式;(2)、求证:∠BOF=∠BDF :(3)、是否存在点M使△MDF为等腰三角形?若不存在,请说明理由;若存在,求ME的长16. 已知二次函数y=ax2+bx+c的图象过点A(﹣1,0),B(3,0),且与y轴交于点C(0,﹣3).
(1)、求抛物线的表达式;(2)、求证:∠BOF=∠BDF :(3)、是否存在点M使△MDF为等腰三角形?若不存在,请说明理由;若存在,求ME的长16. 已知二次函数y=ax2+bx+c的图象过点A(﹣1,0),B(3,0),且与y轴交于点C(0,﹣3). (1)、求此二次函数的表达式及图象顶点D的坐标;(2)、在此抛物线的对称轴上是否存在点E,使△ACE为Rt△,若存在,试求点E的坐标,若不存在,请说明理由;(3)、在平面直角坐标系中,存在点P,满足PA⊥PD,求线段PB的最小值.17. 如图,抛物线 过点 ,与y轴交于点C.
(1)、求此二次函数的表达式及图象顶点D的坐标;(2)、在此抛物线的对称轴上是否存在点E,使△ACE为Rt△,若存在,试求点E的坐标,若不存在,请说明理由;(3)、在平面直角坐标系中,存在点P,满足PA⊥PD,求线段PB的最小值.17. 如图,抛物线 过点 ,与y轴交于点C.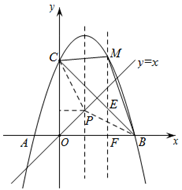 (1)、求抛物线的解析式;(2)、点P为抛物线对称轴上一动点,当 是以BC为底边的等腰三角形时,求点P的坐标;(3)、在(2)条件下,是否存在点M为抛物线第一象限上的点,使得 ?若存在,求出点M的横坐标;若不存在,请说明理由.18. 已知抛物线 与x轴交于A,B两点(点A在点B的左侧).
(1)、求抛物线的解析式;(2)、点P为抛物线对称轴上一动点,当 是以BC为底边的等腰三角形时,求点P的坐标;(3)、在(2)条件下,是否存在点M为抛物线第一象限上的点,使得 ?若存在,求出点M的横坐标;若不存在,请说明理由.18. 已知抛物线 与x轴交于A,B两点(点A在点B的左侧).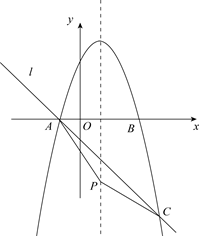 (1)、求点A,点B的坐标;(2)、如图,过点A的直线 与抛物线的另一个交点为C,点P为抛物线对称轴上的一点,连接 ,设点P的纵坐标为m,当 时,求m的值;(3)、将线段AB先向右平移1个单位长度,再向上平移5个单位长度,得到线段MN,若抛物线 与线段MN只有一个交点,请直接写出a的取值范围.19. 如图1,抛物线经过点 , 并交x轴于另一点B,点在第一象限的抛物线上,交直线于点D.
(1)、求点A,点B的坐标;(2)、如图,过点A的直线 与抛物线的另一个交点为C,点P为抛物线对称轴上的一点,连接 ,设点P的纵坐标为m,当 时,求m的值;(3)、将线段AB先向右平移1个单位长度,再向上平移5个单位长度,得到线段MN,若抛物线 与线段MN只有一个交点,请直接写出a的取值范围.19. 如图1,抛物线经过点 , 并交x轴于另一点B,点在第一象限的抛物线上,交直线于点D.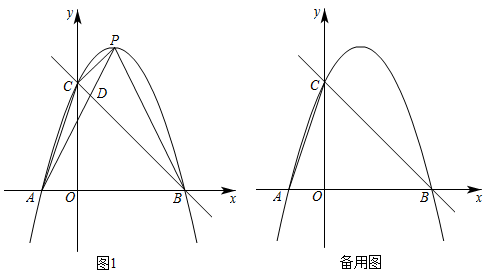 (1)、求该抛物线的函数表达式;(2)、当点P的坐标为时,求四边形的面积;(3)、点Q在抛物线上,当的值最大且是直角三角形时,求点Q的横坐标;20. 某数学兴趣小组运用《几何画板》软件探究y=ax2(a>0)型抛物线图象.发现:如图1所示,该类型图象上任意一点M到定点 F(0,)的距离MF,始终等于它到定直线l:y=﹣上的距离MN(该结论不需要证明),他们称:定点F为图象的焦点,定直线l为图象的准线,y=﹣叫做抛物线的准线方程.其中原点O为FH的中点,FH=2OF= , 例如,抛物线y=x2 , 其焦点坐标为F(0,),准线方程为l:y=﹣.其中MF=MN,FH=2OH=1.
(1)、求该抛物线的函数表达式;(2)、当点P的坐标为时,求四边形的面积;(3)、点Q在抛物线上,当的值最大且是直角三角形时,求点Q的横坐标;20. 某数学兴趣小组运用《几何画板》软件探究y=ax2(a>0)型抛物线图象.发现:如图1所示,该类型图象上任意一点M到定点 F(0,)的距离MF,始终等于它到定直线l:y=﹣上的距离MN(该结论不需要证明),他们称:定点F为图象的焦点,定直线l为图象的准线,y=﹣叫做抛物线的准线方程.其中原点O为FH的中点,FH=2OF= , 例如,抛物线y=x2 , 其焦点坐标为F(0,),准线方程为l:y=﹣.其中MF=MN,FH=2OH=1.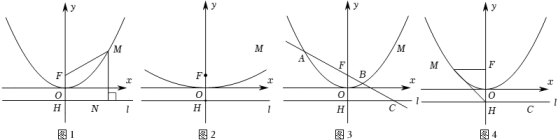 (1)、【基础训练】
(1)、【基础训练】请分别直接写出抛物线y=2x2的焦点坐标和准线l的方程: , .
(2)、【技能训练】如图2所示,已知抛物线y=x2上一点P到准线l的距离为6,求点P的坐标;
(3)、【能力提升】如图3所示,已知过抛物线y=ax2(a>0)的焦点F的直线依次交抛物线及准线l于点A、B、C.若BC=2BF,AF=4,求a的值;
(4)、【拓展升华】古希腊数学家欧多克索斯在深入研究比例理论时,提出了分线段的“中末比”问题:点C将一条线段AB分为两段AC和CB,使得其中较长一段AC是全线段AB与另一段CB的比例中项,即满足:==.后人把这个数称为“黄金分割”把点C称为线段AB的黄金分割点.
如图4所示,抛物线y=x2的焦点F(0,1),准线l与y轴交于点H(0,﹣1),E为线段HF的黄金分割点,点M为y轴左侧的抛物线上一点.当=时,请直接写出△HME的面积值.
21. 如图,和的顶点重合, , , , .

 (1)、特例发现:如图1,当点 , 分别在 , 上时,可以得出结论: , 直线与直线的位置关系是;(2)、探究证明:如图2,将图1中的绕点顺时针旋转,使点恰好落在线段上,连接 , (1)中的结论是否仍然成立?若成立,请证明;若不成立,请说明理由;(3)、拓展运用:如图3,将图1中的绕点顺时针旋转 , 连接、 , 它们的延长线交于点 , 当时,求的值.22. 如图,在平面直角坐标系中,平行四边形ABCD的边AB在x轴上,顶点D在y轴的正半轴上,M为BC的中点,OA、OB的长分别是一元二次方程的两个根 , , 动点P从点D出发以每秒1个单位长度的速度沿折线向点B运动,到达B点停止.设运动时间为t秒,的面积为S.
(1)、特例发现:如图1,当点 , 分别在 , 上时,可以得出结论: , 直线与直线的位置关系是;(2)、探究证明:如图2,将图1中的绕点顺时针旋转,使点恰好落在线段上,连接 , (1)中的结论是否仍然成立?若成立,请证明;若不成立,请说明理由;(3)、拓展运用:如图3,将图1中的绕点顺时针旋转 , 连接、 , 它们的延长线交于点 , 当时,求的值.22. 如图,在平面直角坐标系中,平行四边形ABCD的边AB在x轴上,顶点D在y轴的正半轴上,M为BC的中点,OA、OB的长分别是一元二次方程的两个根 , , 动点P从点D出发以每秒1个单位长度的速度沿折线向点B运动,到达B点停止.设运动时间为t秒,的面积为S.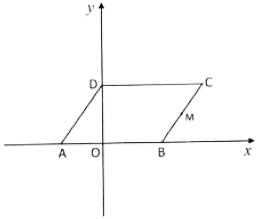 (1)、求点C的坐标;(2)、求S关于t的函数关系式,并写出自变量t的取值范围;(3)、在点P的运动过程中,是否存在点P,使是等腰三角形?若存在,请直接写出点P的坐标;若不存在,请说明理由.23. 我们可以通过面积运算的方法,得到等腰三角形底边上的任意一点到两腰的距离之和与一腰上的高之间的数量关系,并利用这个关系解决相关问题.
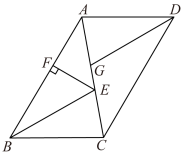
(1)、求点C的坐标;(2)、求S关于t的函数关系式,并写出自变量t的取值范围;(3)、在点P的运动过程中,是否存在点P,使是等腰三角形?若存在,请直接写出点P的坐标;若不存在,请说明理由.23. 我们可以通过面积运算的方法,得到等腰三角形底边上的任意一点到两腰的距离之和与一腰上的高之间的数量关系,并利用这个关系解决相关问题. (1)、如图一,在等腰中, , 边上有一点D,过点D作于E,于F,过点C作于G.利用面积证明: .(2)、如图二,将矩形沿着折叠,使点A与点C重合,点B落在处,点G为折痕上一点,过点G作于M,于N.若 , , 求的长.(3)、如图三,在四边形中,E为线段上的一点, , , 连接 , 且 , , , , 求的长.24. 回顾:用数学的思维思考
(1)、如图一,在等腰中, , 边上有一点D,过点D作于E,于F,过点C作于G.利用面积证明: .(2)、如图二,将矩形沿着折叠,使点A与点C重合,点B落在处,点G为折痕上一点,过点G作于M,于N.若 , , 求的长.(3)、如图三,在四边形中,E为线段上的一点, , , 连接 , 且 , , , , 求的长.24. 回顾:用数学的思维思考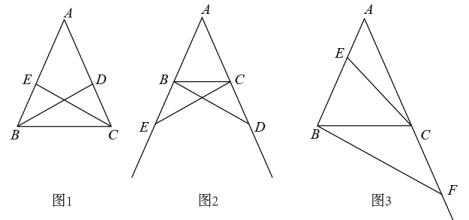 (1)、如图1,在△ABC中,AB=AC.
(1)、如图1,在△ABC中,AB=AC.①BD,CE是△ABC的角平分线.求证:BD=CE.
②点D,E分别是边AC,AB的中点,连接BD,CE.求证:BD=CE.
(从①②两题中选择一题加以证明)
(2)、猜想:用数学的眼光观察经过做题反思,小明同学认为:在△ABC中,AB=AC,D为边AC上一动点(不与点A,C重合).对于点D在边AC上的任意位置,在另一边AB上总能找到一个与其对应的点E,使得BD=CE.进而提出问题:若点D,E分别运动到边AC,AB的延长线上,BD与CE还相等吗?请解决下面的问题:
如图2,在△ABC中,AB=AC,点D,E分别在边AC,AB的延长线上,请添加一个条件(不再添加新的字母),使得BD=CE,并证明.
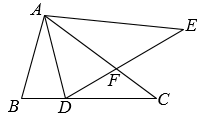
(3)、探究:用数学的语言表达如图3,在△ABC中,AB=AC=2,∠A=36°,E为边AB上任意一点(不与点A,B重合),F为边AC延长线上一点.判断BF与CE能否相等.若能,求CF的取值范围;若不能,说明理由.
25. 和都是等边三角形. (1)、将绕点A旋转到图①的位置时,连接BD,CE并延长相交于点P(点P与点A重合),有(或)成立;请证明.(2)、将绕点A旋转到图②的位置时,连接BD,CE相交于点P,连接PA,猜想线段PA、PB、PC之间有怎样的数量关系?并加以证明;(3)、将绕点A旋转到图③的位置时,连接BD,CE相交于点P,连接PA,猜想线段PA、PB、PC之间有怎样的数量关系?直接写出结论,不需要证明.26. 已知 ,在 内部作等腰 , , .点 为射线 上任意一点(与点 不重合),连接 ,将线段 绕点 逆时针旋转 得到线段 ,连接 并延长交射线 于点 .
(1)、将绕点A旋转到图①的位置时,连接BD,CE并延长相交于点P(点P与点A重合),有(或)成立;请证明.(2)、将绕点A旋转到图②的位置时,连接BD,CE相交于点P,连接PA,猜想线段PA、PB、PC之间有怎样的数量关系?并加以证明;(3)、将绕点A旋转到图③的位置时,连接BD,CE相交于点P,连接PA,猜想线段PA、PB、PC之间有怎样的数量关系?直接写出结论,不需要证明.26. 已知 ,在 内部作等腰 , , .点 为射线 上任意一点(与点 不重合),连接 ,将线段 绕点 逆时针旋转 得到线段 ,连接 并延长交射线 于点 .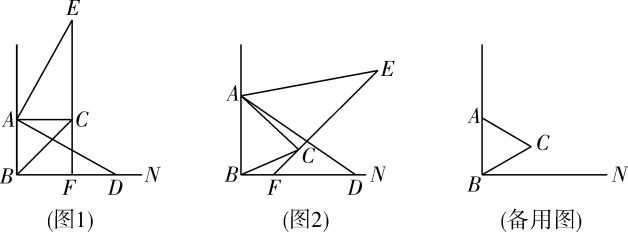 (1)、如图1,当 时,线段 与 的数量关系是;(2)、如图2,当 时,(1)中的结论是否还成立?若成立,请给予证明;若不成立,请说明理由;(3)、若 , , ,过点 作 ,垂足为 ,请直接写出 的长(用含有 的式子表示).27. 如图, 中, , 相交于点 , , 分别是 , 的中点.
(1)、如图1,当 时,线段 与 的数量关系是;(2)、如图2,当 时,(1)中的结论是否还成立?若成立,请给予证明;若不成立,请说明理由;(3)、若 , , ,过点 作 ,垂足为 ,请直接写出 的长(用含有 的式子表示).27. 如图, 中, , 相交于点 , , 分别是 , 的中点. (1)、求证: ;(2)、设 ,当 为何值时,四边形 是矩形?请说明理由.28. 已知抛物线 与 轴交于点 和点 两点,与 轴交于点 .
(1)、求证: ;(2)、设 ,当 为何值时,四边形 是矩形?请说明理由.28. 已知抛物线 与 轴交于点 和点 两点,与 轴交于点 . (1)、求抛物线的解析式;(2)、点 是抛物线上一动点(不与点 , , 重合),作 轴,垂足为 ,连接 .
(1)、求抛物线的解析式;(2)、点 是抛物线上一动点(不与点 , , 重合),作 轴,垂足为 ,连接 .①如图1,若点 在第三象限,且 ,求点 的坐标;
②直线 交直线 于点 ,当点 关于直线 的对称点 落在 轴上时,求四边形 的周长.
29. 综合与实践综合与实践课上,老师让同学们以“矩形的折叠”为主题开展数学活动.


 (1)、操作判断
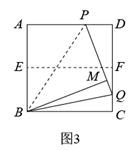
(1)、操作判断操作一:对折矩形纸片ABCD,使AD与BC重合,得到折痕EF,把纸片展平;
操作二:在AD上选一点P,沿BP折叠,使点A落在矩形内部点M处,把纸片展平,连接PM,BM.
根据以上操作,当点M在EF上时,写出图1中一个30°的角:.
(2)、迁移探究小华将矩形纸片换成正方形纸片,继续探究,过程如下:
将正方形纸片ABCD按照(1)中的方式操作,并延长PM交CD于点Q,连接BQ.
①如图2,当点M在EF上时,∠MBQ=▲ °,∠CBQ=▲ °;
②改变点P在AD上的位置(点P不与点A,D重合),如图3,判断∠MBQ与∠CBQ的数量关系,并说明理由.
(3)、拓展应用在(2)的探究中,已知正方形纸片ABCD的边长为8cm,当FQ=1cm时,直接写出AP的长.
30. 如图,是平行四边形的对角线,平分 , 交于点. (1)、请用尺规作的角平分线 , 交于点(要求保留作图痕迹,不写作法,在确认答案后,请用黑色笔将作图痕迹再填涂一次):(2)、根据图形猜想四边形为平行四边形,请将下面的证明过程补充完整.
(1)、请用尺规作的角平分线 , 交于点(要求保留作图痕迹,不写作法,在确认答案后,请用黑色笔将作图痕迹再填涂一次):(2)、根据图形猜想四边形为平行四边形,请将下面的证明过程补充完整.证明:∵四边形是平行四边形,
∴
∵ ▲ .(两线平行,内错角相等).
又∵平分 , 平分 ,
∴ ,
∴.
∴ ▲ ( )(填推理的依据)
又∵四边形是平行四边形.
∴.
∴四边形为平行四边形( )(填推理的依据),
31. 问题背景:一次数学综合实践活动课上,小慧发现并证明了关于三角形角平分线的一个结论.如图1,已知是的角平分线,可证小慧的证明思路是:如图2,过点作 , 交的延长线于点 , 构造相似三角形来证明.
尝试证明:
 (1)、请参照小慧提供的思路,利用图2证明:;(2)、应用拓展:
(1)、请参照小慧提供的思路,利用图2证明:;(2)、应用拓展:
如图3,在中, , 是边上一点.连接 , 将沿所在直线折叠,点恰好落在边上的点处.若 , , 求的长;
若 , , 求的长用含 , 的式子表示.
32. 为提高耕地灌溉效率,小明的爸妈准备在耕地、、、四个位置安装四个自动喷酒装置(如图1所示),、、、四点恰好在边长为50米的正方形的四个顶点上,为了用水管将四个自动喷洒装置相互连通,爸妈设计了如下两个水管铺设方案(各图中实线为铺设的水管).方案一:如图2所示,沿正方形的三边铺设水管;
方案二:如图3所示,沿正方形的两条对角线铺设水管.
 (1)、请通过计算说明上述两方案中哪个方案铺设水管的总长度更短:(2)、小明看了爸妈的方案后,根据“蜂集原理”重新设计了一个方案(如图4所示),
(1)、请通过计算说明上述两方案中哪个方案铺设水管的总长度更短:(2)、小明看了爸妈的方案后,根据“蜂集原理”重新设计了一个方案(如图4所示),满足 , , 、请将小明的方案与爸妈的方案比较,判断谁的方案中铺设水管的总长度更短,并说明理由.(参考数据: , )
33. 如图,在平面直角坐标系中,已知抛物线经过 , 两点,直线与轴交于点.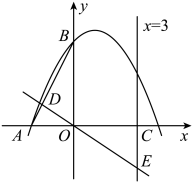 (1)、求 , 的值;(2)、经过点的直线分别与线段 , 直线交于点 , , 且与的面积相等,求直线的解析式;(3)、是抛物线上位于第一象限的一个动点,在线段和直线上是否分别存在点 , , 使 , , , 为顶点的四边形是以为一边的矩形?若存在,求出点的坐标;若不存在,请说明理由.34. 如图,四边形ABCD中, ,∠ABC=90°,∠C=30°,AD=3, ,DH⊥BC于点H . 将△PQM与该四边形按如图方式放在同一平面内,使点P与A重合,点B在PM上,其中∠Q=90°,∠QPM=30°, .
(1)、求 , 的值;(2)、经过点的直线分别与线段 , 直线交于点 , , 且与的面积相等,求直线的解析式;(3)、是抛物线上位于第一象限的一个动点,在线段和直线上是否分别存在点 , , 使 , , , 为顶点的四边形是以为一边的矩形?若存在,求出点的坐标;若不存在,请说明理由.34. 如图,四边形ABCD中, ,∠ABC=90°,∠C=30°,AD=3, ,DH⊥BC于点H . 将△PQM与该四边形按如图方式放在同一平面内,使点P与A重合,点B在PM上,其中∠Q=90°,∠QPM=30°, .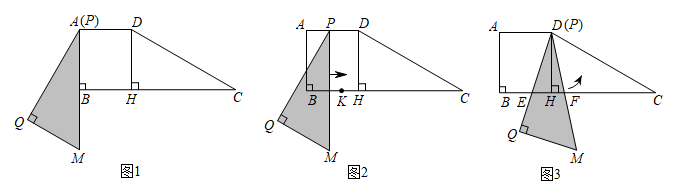 (1)、求证:△PQM≌△CHD;(2)、△PQM从图1的位置出发,先沿着BC方向向右平移(图2),当点P到达点D后立刻绕点D逆时针旋转(图3),当边PM旋转50°时停止.
(1)、求证:△PQM≌△CHD;(2)、△PQM从图1的位置出发,先沿着BC方向向右平移(图2),当点P到达点D后立刻绕点D逆时针旋转(图3),当边PM旋转50°时停止.①边PQ从平移开始,到绕点D旋转结束,求边PQ扫过的面积;
②如图2,点K在BH上,且 .若△PQM右移的速度为每秒1个单位长,绕点D旋转的速度为每秒5°,求点K在△PQM区域(含边界)内的时长;
③如图3.在△PQM旋转过程中,设PQ , PM分别交BC于点E , F , 若BE=d , 直接写出CF的长(用含d的式子表示).
35. 综合与实践(1)、问题情境:在Rt△ABC中,∠BAC=90°,AB=6,AC=8.直角三角板EDF中∠EDF=90°,将三角板的直角顶点D放在Rt△ABC斜边BC的中点处,并将三角板绕点D旋转,三角板的两边DE,DF分别与边AB,AC交于点M,N,猜想证明:
如图①,在三角板旋转过程中,当点M为边AB的中点时,试判断四边形AMDN的形状,并说明理由;
(2)、问题解决:如图②,在三角板旋转过程中,当时,求线段CN的长;
(3)、如图③,在三角板旋转过程中,当AM=AN时,直接写出线段AN的长.36. 如图 (1)、如图1,在△ABC中, ,CD平分 ,交AB于点D, // ,交BC于点E.
(1)、如图1,在△ABC中, ,CD平分 ,交AB于点D, // ,交BC于点E.①若 , ,求BC的长;
②试探究 是否为定值.如果是,请求出这个定值;如果不是,请说明理由.
(2)、如图2, 和 是△ABC的2个外角, ,CD平分 ,交AB的延长线于点D, // ,交CB的延长线于点E.记△ACD的面积为 ,△CDE的面积为 ,△BDE的面积为 .若 ,求 的值.37. 如图,将矩形ABCD沿对角线AC折叠,点B的对应点为E,AE与CD交于点F.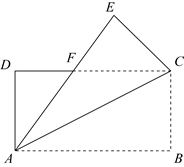 (1)、求证: ;(2)、若 ,求 的度数.38. 如图,二次函数与轴交于 (0,0), (4,0)两点,顶点为 , 连接、 , 若点是线段上一动点,连接 , 将沿折叠后,点落在点的位置,线段与轴交于点 , 且点与、点不重合.
(1)、求证: ;(2)、若 ,求 的度数.38. 如图,二次函数与轴交于 (0,0), (4,0)两点,顶点为 , 连接、 , 若点是线段上一动点,连接 , 将沿折叠后,点落在点的位置,线段与轴交于点 , 且点与、点不重合.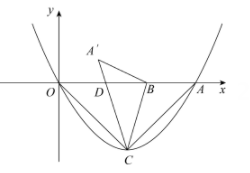 (1)、求二次函数的表达式;(2)、①求证:;
(1)、求二次函数的表达式;(2)、①求证:;②求;
(3)、当时,求直线与二次函数的交点横坐标.