2022年全国中考数学真题分类汇编23 图形的变换(2)
试卷更新日期:2022-12-29 类型:二轮复习
一、单选题
-
1. 下面由北京冬奥会比赛项目图标组成的四个图形中,可看作轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列绿色能源图标中既是轴对称图形又是中心对称图形的是( )A、
2. 下列绿色能源图标中既是轴对称图形又是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 3. 下面用数学家名字命名的图形中,既是轴对称图形,又是中心对称图形的是( )A、
3. 下面用数学家名字命名的图形中,既是轴对称图形,又是中心对称图形的是( )A、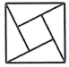 赵爽弦图
B、
赵爽弦图
B、 笛卡尔心形线
C、
笛卡尔心形线
C、 科克曲线
D、
科克曲线
D、 斐波那契螺旋线
4. 如图,在中,是边上的点, , , 则与的周长比是( )
斐波那契螺旋线
4. 如图,在中,是边上的点, , , 则与的周长比是( ) A、 B、 C、 D、5. 2022年2月第24届冬季奥林匹克运动会在我国北京成功举办,以下是参选的冬奥会会徽设计的部分图形,其中既是轴对称图形又是中心对称图形的是( )A、
A、 B、 C、 D、5. 2022年2月第24届冬季奥林匹克运动会在我国北京成功举办,以下是参选的冬奥会会徽设计的部分图形,其中既是轴对称图形又是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 6. 在平面直角坐标系中,点A与点关于轴对称,点A与点关于轴对称.已知点 , 则点的坐标是( )A、 B、 C、 D、7. 如图,若抛物线与x轴交于A、B两点,与y轴交于点C,若.则的值为( )
6. 在平面直角坐标系中,点A与点关于轴对称,点A与点关于轴对称.已知点 , 则点的坐标是( )A、 B、 C、 D、7. 如图,若抛物线与x轴交于A、B两点,与y轴交于点C,若.则的值为( )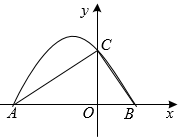 A、 B、 C、 D、8. 已知△ABC与△A1B1C1是位似图形,位似比是1:3,则△ABC与△A1B1C1的面积比( )A、1 :3 B、1:6 C、1:9 D、3:19. 如图,在△ABC中,D,E分别是AB和AC上的点,DE∥BC,若= , 那么=( )
A、 B、 C、 D、8. 已知△ABC与△A1B1C1是位似图形,位似比是1:3,则△ABC与△A1B1C1的面积比( )A、1 :3 B、1:6 C、1:9 D、3:19. 如图,在△ABC中,D,E分别是AB和AC上的点,DE∥BC,若= , 那么=( )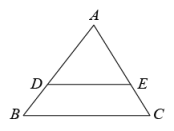 A、 B、 C、 D、10. 在平面直角坐标系中,点与点关于原点成中心对称,则的值为( )A、 B、 C、1 D、311. 如图,相交于点E, , 则的长为( )
A、 B、 C、 D、10. 在平面直角坐标系中,点与点关于原点成中心对称,则的值为( )A、 B、 C、1 D、311. 如图,相交于点E, , 则的长为( ) A、 B、4 C、 D、612. 图中的图形为轴对称图形,该图形的对称轴的条数为( )
A、 B、4 C、 D、612. 图中的图形为轴对称图形,该图形的对称轴的条数为( ) A、1 B、2 C、3 D、513. 下列图案中,不是轴对称图形的是( )A、
A、1 B、2 C、3 D、513. 下列图案中,不是轴对称图形的是( )A、 B、
B、 C、
C、 D、
D、 14. 如图,点 , 将线段先向上平移2个单位长度,再向左平移3个单位长度,得到线段 , 则点的对应点的坐标是( )
14. 如图,点 , 将线段先向上平移2个单位长度,再向左平移3个单位长度,得到线段 , 则点的对应点的坐标是( )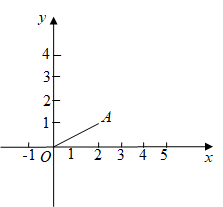 A、 B、 C、 D、15. 如图,中, , 将绕点顺时针旋转得到 , 使点的对应点恰好落在边上,、交于点 . 若 , 则的度数是(用含的代数式表示)( )
A、 B、 C、 D、15. 如图,中, , 将绕点顺时针旋转得到 , 使点的对应点恰好落在边上,、交于点 . 若 , 则的度数是(用含的代数式表示)( )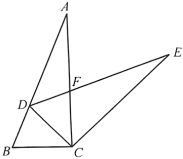 A、 B、 C、 D、16. 下列图形中既是轴对称图形又是中心对称图形的是( )A、
A、 B、 C、 D、16. 下列图形中既是轴对称图形又是中心对称图形的是( )A、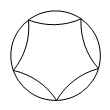 B、
B、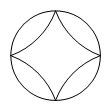 C、
C、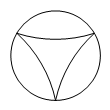 D、
D、 17. 如图,在中, , 将绕点C顺时针旋转得到 , 其中点与点A是对应点,点与点B是对应点.若点恰好落在边上,则点A到直线的距离等于( )
17. 如图,在中, , 将绕点C顺时针旋转得到 , 其中点与点A是对应点,点与点B是对应点.若点恰好落在边上,则点A到直线的距离等于( ) A、 B、 C、3 D、218. 雪花、风车….展示着中心对称的美,利用中心对称,可以探索并证明图形的性质,请思考在下列图形中,是中心对称图形但不一定是轴对称图形的为( )A、扇形 B、平行四边形 C、等边三角形 D、矩形19. 如图,以点O为位似中心,作四边形 的位似图形 ﹐已知 ,若四边形 的面积是2,则四边形 的面积是( )
A、 B、 C、3 D、218. 雪花、风车….展示着中心对称的美,利用中心对称,可以探索并证明图形的性质,请思考在下列图形中,是中心对称图形但不一定是轴对称图形的为( )A、扇形 B、平行四边形 C、等边三角形 D、矩形19. 如图,以点O为位似中心,作四边形 的位似图形 ﹐已知 ,若四边形 的面积是2,则四边形 的面积是( )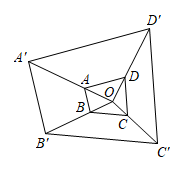 A、4 B、6 C、16 D、1820. 如图,在 中, ,则 的值是( )
A、4 B、6 C、16 D、1820. 如图,在 中, ,则 的值是( )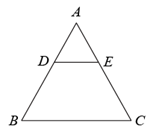 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
21. 希腊数学家海伦给出了挖掘直线隧道的方法:如图,A,B是两侧山脚的入口,从B出发任作线段BC,过C作CD⊥BC,然后依次作垂线段DE,EF,FG,GH,直到接近点A,作AJ⊥GH于点J.每条线段可测量,长度如图所示.分别在BC,AJ上任选点M,N,作MQ⊥BC,NP⊥AJ,使得 , 此时点P,A,B,Q共线.挖隧道时始终能看见P,Q处的标志即可.
 (1)、 km.(2)、 = .22. 如图,在△ABC中,∠C=90°,∠B=30°,AB=6,将△ABC绕点A逆时针方向旋转15°得到△AB′C′,B′C′交AB于点E,则B′E= .
(1)、 km.(2)、 = .22. 如图,在△ABC中,∠C=90°,∠B=30°,AB=6,将△ABC绕点A逆时针方向旋转15°得到△AB′C′,B′C′交AB于点E,则B′E= .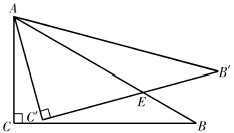 23. 《墨子·天文志》记载:“执规矩,以度天下之方圆.”度方知圆,感悟数学之美.如图,正方形的面积为4,以它的对角线的交点为位似中心,作它的位似图形 , 若 , 则四边形的外接圆的周长为 .
23. 《墨子·天文志》记载:“执规矩,以度天下之方圆.”度方知圆,感悟数学之美.如图,正方形的面积为4,以它的对角线的交点为位似中心,作它的位似图形 , 若 , 则四边形的外接圆的周长为 .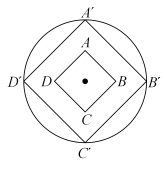 24. 如图,在四边形中,对角线 , 相交于点 , , .若 , 则的面积是 , 度.
24. 如图,在四边形中,对角线 , 相交于点 , , .若 , 则的面积是 , 度. 25. 数学兴趣小组通过测量旗杆的影长来求旗杆的高度,他们在某一时刻测得高为2米的标杆影长为1.2米,此时旗杆影长为7.2米,则旗杆的高度为米.
25. 数学兴趣小组通过测量旗杆的影长来求旗杆的高度,他们在某一时刻测得高为2米的标杆影长为1.2米,此时旗杆影长为7.2米,则旗杆的高度为米. 26. 如图,在矩形中,若 , 则的长为 .
26. 如图,在矩形中,若 , 则的长为 . 27. 如图,为了测量校园内旗杆AB的高度,九年级数学应用实践小组,根据光的反射定律,利用镜子、皮尺和测角仪等工具,按以下方式进行测量:把镜子放在点O处,然后观测者沿着水平直线BO后退到点D,这时恰好能在镜子里看到旗杆顶点A,此时测得观测者观看镜子的俯角α=60°,观测者眼睛与地面距离CD=1.7m,BD=11m,则旗杆AB的高度约为m.(结果取整数,)
27. 如图,为了测量校园内旗杆AB的高度,九年级数学应用实践小组,根据光的反射定律,利用镜子、皮尺和测角仪等工具,按以下方式进行测量:把镜子放在点O处,然后观测者沿着水平直线BO后退到点D,这时恰好能在镜子里看到旗杆顶点A,此时测得观测者观看镜子的俯角α=60°,观测者眼睛与地面距离CD=1.7m,BD=11m,则旗杆AB的高度约为m.(结果取整数,) 28. 如图,在平面直角坐标系中, 为等腰三角形, ,点B到x轴的距离为4,若将 绕点O逆时针旋转 ,得到 ,则点 的坐标为.
28. 如图,在平面直角坐标系中, 为等腰三角形, ,点B到x轴的距离为4,若将 绕点O逆时针旋转 ,得到 ,则点 的坐标为. 29. 古希腊数学家泰勒斯曾利用立杆测影的方法,在金字塔影子的顶部直立一根木杆,借助太阳光测金字塔的高度.如图,木杆EF长2米,它的影长FD是4米,同一时刻测得OA是268米,则金字塔的高度BO是米.
29. 古希腊数学家泰勒斯曾利用立杆测影的方法,在金字塔影子的顶部直立一根木杆,借助太阳光测金字塔的高度.如图,木杆EF长2米,它的影长FD是4米,同一时刻测得OA是268米,则金字塔的高度BO是米.
三、作图题
-
30. 图①,图②均是的正方形网格,每个小正方形的顶点称为格点.其中点 , , 均在格点上.请在给定的网格中按要求画四边形.
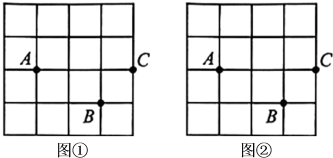 (1)、在图①中,找一格点 , 使以点 , , , 为顶点的四边形是轴对称图形;(2)、在图②中,找一格点 , 使以点 , , , 为顶点的四边形是中心对称图形.31. 如图,方格纸中每个小正方形的边长均为1,的顶点和线段的端点均在小正方形的顶点上.
(1)、在图①中,找一格点 , 使以点 , , , 为顶点的四边形是轴对称图形;(2)、在图②中,找一格点 , 使以点 , , , 为顶点的四边形是中心对称图形.31. 如图,方格纸中每个小正方形的边长均为1,的顶点和线段的端点均在小正方形的顶点上.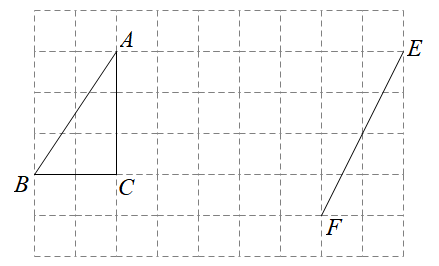
⑴在方格纸中面出 , 使与关于直线对称(点D在小正方形的顶点上);
⑵在方格纸中画出以线段为一边的平行四边形(点G,点H均在小正方形的顶点上),且平行四边形的面积为4.连接 , 请直接写出线段的长.
四、综合题
-
32. 如图,直线分别与x轴、y轴交于点A、B,点C为线段上一动点(不与A、B重合),以C为顶点作 , 射线交线段于点D,将射线绕点O顺时针旋转交射线于点E,连接.
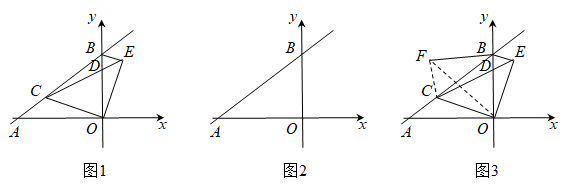 (1)、证明:;(用图1)(2)、当为直角三角形时,求的长度;(用图2)(3)、点A关于射线的对称点为F,求的最小值.(用图3)33. 已知二次函数图象的顶点坐标为 , 且与x轴交于点 .
(1)、证明:;(用图1)(2)、当为直角三角形时,求的长度;(用图2)(3)、点A关于射线的对称点为F,求的最小值.(用图3)33. 已知二次函数图象的顶点坐标为 , 且与x轴交于点 . (1)、求二次函数的表达式;(2)、如图,将二次函数图象绕x轴的正半轴上一点旋转 , 此时点A、B的对应点分别为点C、D.
(1)、求二次函数的表达式;(2)、如图,将二次函数图象绕x轴的正半轴上一点旋转 , 此时点A、B的对应点分别为点C、D.①连结 , 当四边形为矩形时,求m的值;
②在①的条件下,若点M是直线上一点,原二次函数图象上是否存在一点Q,使得以点B、C、M、Q为顶点的四边形为平行四边形,若存在,求出点Q的坐标;若不存在,请说明理由.
34. 在平面直角坐标系中,O为坐标原点,抛物线与y轴交于点. (1)、直接写出抛物线的解析式.(2)、如图,将抛物线向左平移1个单位长度,记平移后的抛物线顶点为Q,平移后的抛物线与x轴交于A、B两点(点A在点B的右侧),与y轴交于点C.判断以B、C、Q三点为顶点的三角形是否为直角三角形,并说明理由.(3)、直线BC与抛物线交于M、N两点(点N在点M的右侧),请探究在x轴上是否存在点T,使得以B、N、T三点为顶点的三角形与相似,若存在,请求出点T的坐标;若不存在,请说明理由.(4)、若将抛物线进行适当的平移,当平移后的抛物线与直线BC最多只有一个公共点时,请直接写出拋物线平移的最短距离并求出此时抛物线的顶点坐标.35. 如图,抛物线y=﹣x2+3x+4与x轴交于A,B两点(点A位于点B的左侧),与y轴交于C点,抛物线的对称轴l与x轴交于点N,长为1的线段PQ(点P位于点Q的上方)在x轴上方的抛物线对称轴上运动.
(1)、直接写出抛物线的解析式.(2)、如图,将抛物线向左平移1个单位长度,记平移后的抛物线顶点为Q,平移后的抛物线与x轴交于A、B两点(点A在点B的右侧),与y轴交于点C.判断以B、C、Q三点为顶点的三角形是否为直角三角形,并说明理由.(3)、直线BC与抛物线交于M、N两点(点N在点M的右侧),请探究在x轴上是否存在点T,使得以B、N、T三点为顶点的三角形与相似,若存在,请求出点T的坐标;若不存在,请说明理由.(4)、若将抛物线进行适当的平移,当平移后的抛物线与直线BC最多只有一个公共点时,请直接写出拋物线平移的最短距离并求出此时抛物线的顶点坐标.35. 如图,抛物线y=﹣x2+3x+4与x轴交于A,B两点(点A位于点B的左侧),与y轴交于C点,抛物线的对称轴l与x轴交于点N,长为1的线段PQ(点P位于点Q的上方)在x轴上方的抛物线对称轴上运动.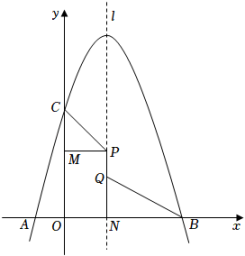 (1)、直接写出A,B,C三点的坐标;(2)、求CP+PQ+QB的最小值;(3)、过点P作PM⊥y轴于点M,当CPM和QBN相似时,求点Q的坐标.36. 在平面直角坐标系中,点O为坐标原点,抛物线经过点 , 点 , 与y轴交于点C.
(1)、直接写出A,B,C三点的坐标;(2)、求CP+PQ+QB的最小值;(3)、过点P作PM⊥y轴于点M,当CPM和QBN相似时,求点Q的坐标.36. 在平面直角坐标系中,点O为坐标原点,抛物线经过点 , 点 , 与y轴交于点C.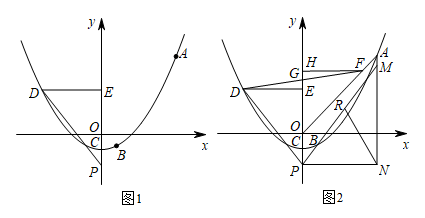 (1)、求a,b的值;(2)、如图1,点D在该抛物线上,点D的横坐标为 , 过点D向y轴作垂线,垂足为点E.点P为y轴负半轴上的一个动点,连接、设点P的纵坐标为t,的面积为S,求S关于t的函数解析式(不要求写出自变量t的取值范围);(3)、如图2,在(2)的条件下,连接 , 点F在上,过点F向y轴作垂线,垂足为点H,连接交y轴于点G,点G为的中点,过点A作y轴的平行线与过点P所作的x轴的平行线相交于点N,连接 , , 延长交于点M,点R在上,连接 , 若 , , 求直线的解析式.37. 已知二次函数 图象的对称轴与x轴交于点A(1,0),图象与y轴交于点B(0,3),C、D为该二次函数图象上的两个动点(点C在点D的左侧),且 .
(1)、求a,b的值;(2)、如图1,点D在该抛物线上,点D的横坐标为 , 过点D向y轴作垂线,垂足为点E.点P为y轴负半轴上的一个动点,连接、设点P的纵坐标为t,的面积为S,求S关于t的函数解析式(不要求写出自变量t的取值范围);(3)、如图2,在(2)的条件下,连接 , 点F在上,过点F向y轴作垂线,垂足为点H,连接交y轴于点G,点G为的中点,过点A作y轴的平行线与过点P所作的x轴的平行线相交于点N,连接 , , 延长交于点M,点R在上,连接 , 若 , , 求直线的解析式.37. 已知二次函数 图象的对称轴与x轴交于点A(1,0),图象与y轴交于点B(0,3),C、D为该二次函数图象上的两个动点(点C在点D的左侧),且 . (1)、求该二次函数的表达式;(2)、若点C与点B重合,求tan∠CDA的值;(3)、点C是否存在其他的位置,使得tan∠CDA的值与(2)中所求的值相等?若存在,请求出点C的坐标;若不存在,请说明理由.38. 如图,已知抛物线: 与x轴交于点A, (A在B的左侧),与y轴交于点C,对称轴是直线 ,P是第一象限内抛物线上的任一点.
(1)、求该二次函数的表达式;(2)、若点C与点B重合,求tan∠CDA的值;(3)、点C是否存在其他的位置,使得tan∠CDA的值与(2)中所求的值相等?若存在,请求出点C的坐标;若不存在,请说明理由.38. 如图,已知抛物线: 与x轴交于点A, (A在B的左侧),与y轴交于点C,对称轴是直线 ,P是第一象限内抛物线上的任一点.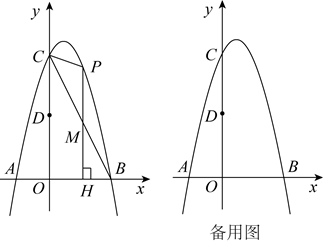 (1)、求抛物线的解析式;(2)、若点D为线段 的中点,则 能否是等边三角形?请说明理由;(3)、过点P作x轴的垂线与线段 交于点M,垂足为点H,若以P,M,C为顶点的三角形与 相似,求点P的坐标.39. 如图,在平面直角坐标系中,直线 分别与x,y轴交于点A,B,抛物线 恰好经过这两点.
(1)、求抛物线的解析式;(2)、若点D为线段 的中点,则 能否是等边三角形?请说明理由;(3)、过点P作x轴的垂线与线段 交于点M,垂足为点H,若以P,M,C为顶点的三角形与 相似,求点P的坐标.39. 如图,在平面直角坐标系中,直线 分别与x,y轴交于点A,B,抛物线 恰好经过这两点. (1)、求此抛物线的解析式;(2)、若点C的坐标是 ,将 绕着点C逆时针旋转90°得到 ,点A的对应点是点E.
(1)、求此抛物线的解析式;(2)、若点C的坐标是 ,将 绕着点C逆时针旋转90°得到 ,点A的对应点是点E.①写出点E的坐标,并判断点E是否在此抛物线上;
②若点P是y轴上的任一点,求 取最小值时,点P的坐标.
40. 如图1,在平面直角坐标系中,Rt△OAB的直角边OA在y轴的正半轴上,且OA=6,斜边OB=10,点P为线段AB上一动点.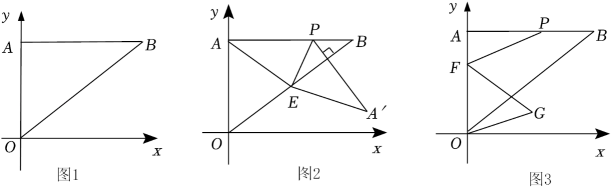 (1)、请直接写出点B的坐标;(2)、若动点P满足∠POB=45°,求此时点P的坐标;(3)、如图2,若点E为线段OB的中点,连接PE,以PE为折痕,在平面内将△APE折叠,点A的对应点为A',当PA'⊥OB时,求此时点P的坐标;(4)、如图3,若F为线段AO上一点,且AF=2,连接FP,将线段FP绕点F顺时针方向旋转60°得线段FG,连接OG,当OG取最小值时,请直接写出OG的最小值和此时线段FP扫过的面积.
(1)、请直接写出点B的坐标;(2)、若动点P满足∠POB=45°,求此时点P的坐标;(3)、如图2,若点E为线段OB的中点,连接PE,以PE为折痕,在平面内将△APE折叠,点A的对应点为A',当PA'⊥OB时,求此时点P的坐标;(4)、如图3,若F为线段AO上一点,且AF=2,连接FP,将线段FP绕点F顺时针方向旋转60°得线段FG,连接OG,当OG取最小值时,请直接写出OG的最小值和此时线段FP扫过的面积.