2022年全国中考数学真题分类汇编23 图形的变换(1)
试卷更新日期:2022-12-29 类型:二轮复习
一、单选题
-
1. 下列图案是轴对称图形但不是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列图形中是轴对称图形的是( )A、
2. 下列图形中是轴对称图形的是( )A、 B、
B、 C、
C、 D、
D、 3. 下列图形是中心对称图形的是( )A、
3. 下列图形是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 4. 如图,在平面直角坐标系中,为的边上一点, , 过作交于点 , 、两点纵坐标分别为1、3,则点的纵坐标为( )
4. 如图,在平面直角坐标系中,为的边上一点, , 过作交于点 , 、两点纵坐标分别为1、3,则点的纵坐标为( )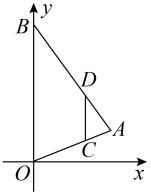 A、4 B、5 C、6 D、75. 七巧板是我国的一种传统智力玩具,下列用七巧板拼成的图形是轴对称图形的是( )A、
A、4 B、5 C、6 D、75. 七巧板是我国的一种传统智力玩具,下列用七巧板拼成的图形是轴对称图形的是( )A、 B、
B、 C、
C、 D、
D、 6. 下面四幅图是我国一些博物馆的标志,其中既是轴对称图形又是中心对称图形的是( )A、温州博物馆
6. 下面四幅图是我国一些博物馆的标志,其中既是轴对称图形又是中心对称图形的是( )A、温州博物馆 B、西藏博物馆
B、西藏博物馆 C、广东博物馆
C、广东博物馆 D、湖北博物馆
D、湖北博物馆 7. 如图,将三角尺直立举起靠近墙面,打开手机手电筒照射三角尺,在墙面上形成影子.则三角尺与影子之间属于以下哪种图形变换( )
7. 如图,将三角尺直立举起靠近墙面,打开手机手电筒照射三角尺,在墙面上形成影子.则三角尺与影子之间属于以下哪种图形变换( )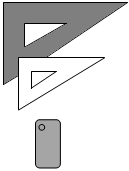 A、平移 B、轴对称 C、旋转 D、位似8. 襄阳市正在创建全国文明城市,某社区从今年6月1日起实施垃扱分类回收.下列图形分别是可回收物、厨余垃圾、有害垃圾及其它垃圾的标志,其中,既是中心对称图形又是轴对称图形的是( )A、
A、平移 B、轴对称 C、旋转 D、位似8. 襄阳市正在创建全国文明城市,某社区从今年6月1日起实施垃扱分类回收.下列图形分别是可回收物、厨余垃圾、有害垃圾及其它垃圾的标志,其中,既是中心对称图形又是轴对称图形的是( )A、 B、
B、 C、
C、 D、
D、 9. 下列汉字中,能看成轴对称图形的是( )A、坡 B、上 C、草 D、原10. 在平面直角坐标系中,点关于y轴对称的点的坐标是( )A、 B、 C、 D、11. 山东省第二十五届运动会将于2022年8月25日在日照市开幕,“全民健身与省运同行”成为日照市当前的运动主题.在下列给出的运动图片中,是轴对称图形的是( )A、
9. 下列汉字中,能看成轴对称图形的是( )A、坡 B、上 C、草 D、原10. 在平面直角坐标系中,点关于y轴对称的点的坐标是( )A、 B、 C、 D、11. 山东省第二十五届运动会将于2022年8月25日在日照市开幕,“全民健身与省运同行”成为日照市当前的运动主题.在下列给出的运动图片中,是轴对称图形的是( )A、 B、
B、 C、
C、 D、
D、 12. 已知 , ,若 ,则 ( )A、4 B、6 C、8 D、1613. 下列分别是2022年北京冬奥会、1998年长野冬奥会、1992年阿尔贝维尔冬奥运会、1984年萨拉热窝冬奥会会徽上的图案,其中是轴对称图形的是( )A、
12. 已知 , ,若 ,则 ( )A、4 B、6 C、8 D、1613. 下列分别是2022年北京冬奥会、1998年长野冬奥会、1992年阿尔贝维尔冬奥运会、1984年萨拉热窝冬奥会会徽上的图案,其中是轴对称图形的是( )A、 B、
B、 C、
C、 D、
D、 14. 下列四幅照片中,主体建筑的构图不对称的是( )A、
14. 下列四幅照片中,主体建筑的构图不对称的是( )A、 B、
B、 C、
C、 D、
D、 15. 下列交通标志中,是轴对称图形的是( )A、
15. 下列交通标志中,是轴对称图形的是( )A、 B、
B、 C、
C、 D、
D、 16. 如图,将△ABC先向右平移1个单位,再绕点P按顺时针方向旋转90°,得到△A′B′C′,则点B的对应点B′的坐标是( )
16. 如图,将△ABC先向右平移1个单位,再绕点P按顺时针方向旋转90°,得到△A′B′C′,则点B的对应点B′的坐标是( ) A、(4,0) B、(2,﹣2) C、(4,﹣1) D、(2,﹣3)17. 下列图形中,是中心对称图形的是( )A、
A、(4,0) B、(2,﹣2) C、(4,﹣1) D、(2,﹣3)17. 下列图形中,是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 18. 秦兵马俑的发现被誉为“世界第八大奇迹”,兵马俑的眼睛到下巴的距离与头顶到下巴的距离之比约为 , 下列估算正确的是( )
18. 秦兵马俑的发现被誉为“世界第八大奇迹”,兵马俑的眼睛到下巴的距离与头顶到下巴的距离之比约为 , 下列估算正确的是( ) A、 B、 C、 D、19. 冬季奥林匹克运动会是世界上规模最大的冬季综合性运动会,下列四个图是历届冬奥会图标中的一部分,其中是轴对称图形的为( )A、
A、 B、 C、 D、19. 冬季奥林匹克运动会是世界上规模最大的冬季综合性运动会,下列四个图是历届冬奥会图标中的一部分,其中是轴对称图形的为( )A、 B、
B、 C、
C、 D、
D、 20. 如图,在直角坐标系中,线段是将绕着点逆时针旋转一定角度后得到的的一部分,则点的对应点的坐标是( )
20. 如图,在直角坐标系中,线段是将绕着点逆时针旋转一定角度后得到的的一部分,则点的对应点的坐标是( )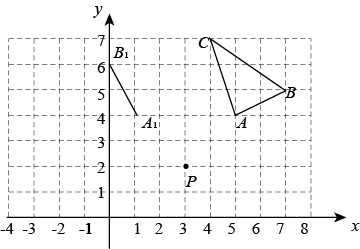 A、(-2,3) B、(-3,2) C、(-2,4) D、(-3,3)21. 如图,一次函数的图象与x轴,y轴分别交于点A,B,点是x轴上一点,点E,F分别为直线和y轴上的两个动点,当周长最小时,点E,F的坐标分别为( )
A、(-2,3) B、(-3,2) C、(-2,4) D、(-3,3)21. 如图,一次函数的图象与x轴,y轴分别交于点A,B,点是x轴上一点,点E,F分别为直线和y轴上的两个动点,当周长最小时,点E,F的坐标分别为( )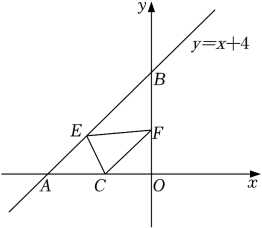 A、 , B、 , C、 , D、 ,22. 如图,点D为边上任一点,交于点E,连接相交于点F,则下列等式中不成立的是( )
A、 , B、 , C、 , D、 ,22. 如图,点D为边上任一点,交于点E,连接相交于点F,则下列等式中不成立的是( ) A、 B、 C、 D、23. 如图,在平面直角坐标系中,点B、C、E在y轴上,点C的坐标为(0,1),AC=2,Rt△ODE是Rt△ABC经过某些变换得到的,则正确的变换是( )
A、 B、 C、 D、23. 如图,在平面直角坐标系中,点B、C、E在y轴上,点C的坐标为(0,1),AC=2,Rt△ODE是Rt△ABC经过某些变换得到的,则正确的变换是( )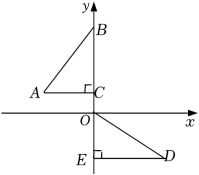 A、△ABC绕点C逆时针旋转90°,再向下平移1个单位 B、△ABC绕点C顺时针旋转90°,再向下平移1个单位 C、△ABC绕点C逆时针旋转90°,再向下平移3个单位 D、△ABC绕点C顺时针旋转90°,再向下平移3个单位
A、△ABC绕点C逆时针旋转90°,再向下平移1个单位 B、△ABC绕点C顺时针旋转90°,再向下平移1个单位 C、△ABC绕点C逆时针旋转90°,再向下平移3个单位 D、△ABC绕点C顺时针旋转90°,再向下平移3个单位二、填空题
-
24. 如图,在平面直角坐标系中,与位似,位似中心是坐标原点O.若点 , 点 , 则与周长的比值是 .
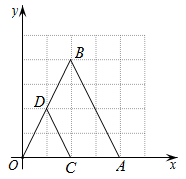 25. 在平面直角坐标系中,已知点P(﹣3,5)与点Q(3,m﹣2)关于原点对称,则m= .26. 如图,在正方形 中, , 是 的中点,点 是正方形内一个动点,且 ,连接 ,将线段 绕点 逆时针旋转 得到线段 ,连接 ,则线段 长的最小值为 .
25. 在平面直角坐标系中,已知点P(﹣3,5)与点Q(3,m﹣2)关于原点对称,则m= .26. 如图,在正方形 中, , 是 的中点,点 是正方形内一个动点,且 ,连接 ,将线段 绕点 逆时针旋转 得到线段 ,连接 ,则线段 长的最小值为 .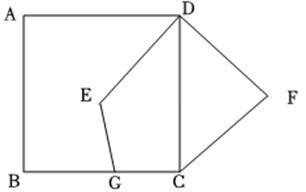 27. 如图,在平面直角坐标系中,点A的坐标是 , 将线段向右平移4个单位长度,得到线段 , 点A的对应点C的坐标是 .
27. 如图,在平面直角坐标系中,点A的坐标是 , 将线段向右平移4个单位长度,得到线段 , 点A的对应点C的坐标是 .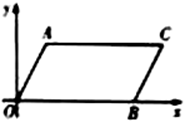 28. 已知是直角三角形,连接以为底作直角三角形且是边上的一点,连接和且则长为 .
28. 已知是直角三角形,连接以为底作直角三角形且是边上的一点,连接和且则长为 . 29. 如图, , , 相交于点 , 若 , , 则的长为 .
29. 如图, , , 相交于点 , 若 , , 则的长为 .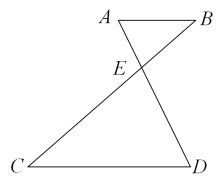 30. 如图,在中,点F、G在上,点E、H分别在、上,四边形是矩形,是的高. , 那么的长为 .
30. 如图,在中,点F、G在上,点E、H分别在、上,四边形是矩形,是的高. , 那么的长为 .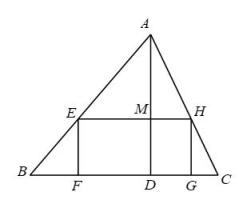
三、解答题
-
31. 如图,在与中,点、分别在边、上,且 , 若 ▲ , 则 . 请从①;②;③这三个选项中选择一个作为条件(写序号),并加以证明.
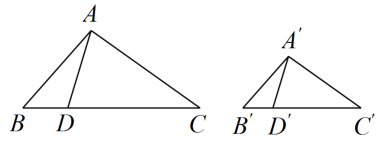 32. 如图,在中, , E是边AC上一点,且 , 过点A作BE的垂线,交BE的延长线于点D,求证: .
32. 如图,在中, , E是边AC上一点,且 , 过点A作BE的垂线,交BE的延长线于点D,求证: .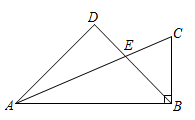
四、综合题
-
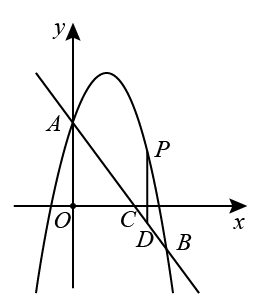
33. 如图(1),二次函数的图象与轴交于、两点,与轴交于点,点的坐标为 , 点的坐标为 , 直线经过、两点.

 (1)、求该二次函数的表达式及其图象的顶点坐标;(2)、点为直线上的一点,过点作轴的垂线与该二次函数的图象相交于点 , 再过点作轴的垂线与该二次函数的图象相交于另一点 , 当时,求点的横坐标;(3)、如图(2),点关于轴的对称点为点 , 点为线段上的一个动点,连接 , 点为线段上一点,且 , 连接 , 当的值最小时,直接写出的长.34. 在平面直角坐标系中,抛物线y=﹣ +(m﹣1)x+2m与x轴交于A,B(4,0)两点,与y轴交于点C,点P是抛物线在第一象限内的一个动点.
(1)、求该二次函数的表达式及其图象的顶点坐标;(2)、点为直线上的一点,过点作轴的垂线与该二次函数的图象相交于点 , 再过点作轴的垂线与该二次函数的图象相交于另一点 , 当时,求点的横坐标;(3)、如图(2),点关于轴的对称点为点 , 点为线段上的一个动点,连接 , 点为线段上一点,且 , 连接 , 当的值最小时,直接写出的长.34. 在平面直角坐标系中,抛物线y=﹣ +(m﹣1)x+2m与x轴交于A,B(4,0)两点,与y轴交于点C,点P是抛物线在第一象限内的一个动点.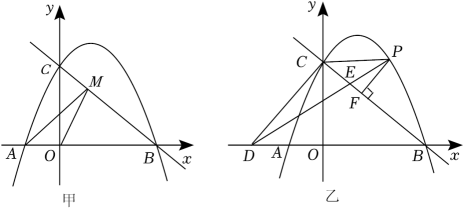 (1)、求抛物线的解析式,并直接写出点A,C的坐标;(2)、如图甲,点M是直线BC上的一个动点,连接AM,OM,是否存在点M使AM+OM最小,若存在,请求出点M的坐标,若不存在,请说明理由;(3)、如图乙,过点P作PF⊥BC,垂足为F,过点C作CD⊥BC,交x轴于点D,连接DP交BC于点E,连接CP.设△PEF的面积为S1 , △PEC的面积为S2 , 是否存在点P,使得最大,若存在,请求出点P的坐标,若不存在,请说明理由.35. 如图,抛物线与坐标轴分别交于A,B,C三点,P是第一象限内抛物线上的一点且横坐标为m.
(1)、求抛物线的解析式,并直接写出点A,C的坐标;(2)、如图甲,点M是直线BC上的一个动点,连接AM,OM,是否存在点M使AM+OM最小,若存在,请求出点M的坐标,若不存在,请说明理由;(3)、如图乙,过点P作PF⊥BC,垂足为F,过点C作CD⊥BC,交x轴于点D,连接DP交BC于点E,连接CP.设△PEF的面积为S1 , △PEC的面积为S2 , 是否存在点P,使得最大,若存在,请求出点P的坐标,若不存在,请说明理由.35. 如图,抛物线与坐标轴分别交于A,B,C三点,P是第一象限内抛物线上的一点且横坐标为m.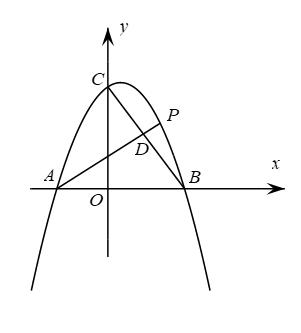 (1)、A,B,C三点的坐标为 , , ;(2)、连接 , 交线段于点D,
(1)、A,B,C三点的坐标为 , , ;(2)、连接 , 交线段于点D,①当与x轴平行时,求的值;
②当与x轴不平行时,求的最大值;
(3)、连接 , 是否存在点P,使得 , 若存在,求m的值,若不存在,请说明理由.36. 已知抛物线 与 轴交于 , 两点,与 轴交于点 .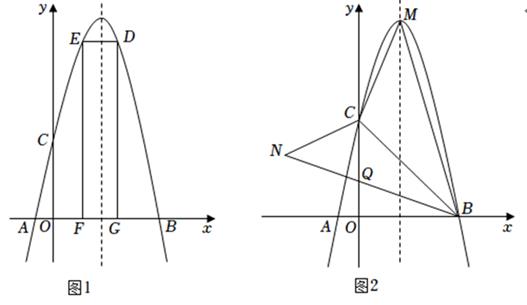 (1)、求 , , 的值;(2)、如图 ,点 是抛物线上位于对称轴右侧的一个动点,且点 在第一象限内,过点 作 轴的平行线交抛物线于点 ,作 轴的平行线交 轴于点 ,过点 作 轴,垂足为点 ,当四边形 的周长最大时,求点 的坐标;(3)、如图 ,点 是抛物线的顶点,将 沿 翻折得到 , 与 轴交于点 ,在对称轴上找一点 ,使得 是以 为直角边的直角三角形,求出所有符合条件的点 的坐标.37. 已知△ABC中,∠ACB=90°,AC=BC=4cm,点P从点A出发,沿AB方向以每秒cm的速度向终点B运动,同时动点Q从点B出发沿BC方向以每秒1cm的速度向终点C运动,设运动的时间为t秒.
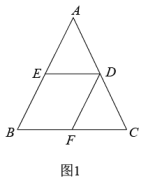
(1)、求 , , 的值;(2)、如图 ,点 是抛物线上位于对称轴右侧的一个动点,且点 在第一象限内,过点 作 轴的平行线交抛物线于点 ,作 轴的平行线交 轴于点 ,过点 作 轴,垂足为点 ,当四边形 的周长最大时,求点 的坐标;(3)、如图 ,点 是抛物线的顶点,将 沿 翻折得到 , 与 轴交于点 ,在对称轴上找一点 ,使得 是以 为直角边的直角三角形,求出所有符合条件的点 的坐标.37. 已知△ABC中,∠ACB=90°,AC=BC=4cm,点P从点A出发,沿AB方向以每秒cm的速度向终点B运动,同时动点Q从点B出发沿BC方向以每秒1cm的速度向终点C运动,设运动的时间为t秒.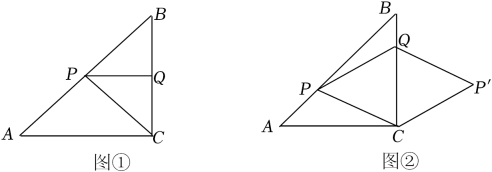 (1)、如图①,若PQ⊥BC,求t的值;(2)、如图②,将△PQC沿BC翻折至△P′QC,当t为何值时,四边形QPCP′为菱形?38. 如图1,△ABC是等边三角形,点D在△ABC的内部,连接AD,将线段AD绕点A按逆时针方向旋转60°,得到线段AE,连接BD,DE,CE.
(1)、如图①,若PQ⊥BC,求t的值;(2)、如图②,将△PQC沿BC翻折至△P′QC,当t为何值时,四边形QPCP′为菱形?38. 如图1,△ABC是等边三角形,点D在△ABC的内部,连接AD,将线段AD绕点A按逆时针方向旋转60°,得到线段AE,连接BD,DE,CE. (1)、判断线段BD与CE的数量关系并给出证明;(2)、延长ED交直线BC于点F.
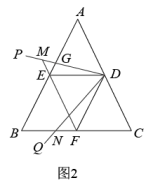
(1)、判断线段BD与CE的数量关系并给出证明;(2)、延长ED交直线BC于点F.①如图2,当点F与点B重合时,直接用等式表示线段AE,BE和CE的数量关系为 ▲ ;
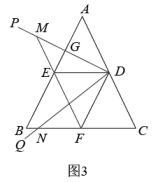
②如图3,当点F为线段BC中点,且ED=EC时,猜想∠BAD的度数,并说明理由.