2022年全国中考数学真题分类汇编21 锐角三角函数
试卷更新日期:2022-12-29 类型:二轮复习
一、单选题
-
1. 如图,一条河两岸互相平行,为测得此河的宽度PT(PT与河岸PQ垂直),测P、Q两点距离为m米, , 则河宽PT的长度是( )
 A、 B、 C、 D、2. 数学活动小组到某广场测量标志性建筑AB的高度.如图,他们在地面上C点测得最高点A的仰角为22°,再向前70m至D点,又测得最高点A的仰角为58°,点C,D,B在同一直线上,则该建筑物AB的高度约为( )(精确到1m.参考数据: , , , )
A、 B、 C、 D、2. 数学活动小组到某广场测量标志性建筑AB的高度.如图,他们在地面上C点测得最高点A的仰角为22°,再向前70m至D点,又测得最高点A的仰角为58°,点C,D,B在同一直线上,则该建筑物AB的高度约为( )(精确到1m.参考数据: , , , )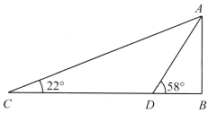 A、28m B、34m C、37m D、46m3. 如图是长春市人民大街下穿隧道工程施工现场的一台起重机的示意图,该起重机的变幅索顶端记为点A,变幅索的底端记为点B,垂直地面,垂足为点D, , 垂足为点C.设 , 下列关系式正确的是( )
A、28m B、34m C、37m D、46m3. 如图是长春市人民大街下穿隧道工程施工现场的一台起重机的示意图,该起重机的变幅索顶端记为点A,变幅索的底端记为点B,垂直地面,垂足为点D, , 垂足为点C.设 , 下列关系式正确的是( )
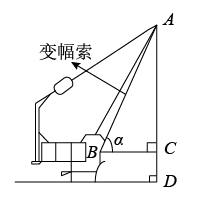 A、 B、 C、 D、4. 如图,某数学兴趣小组测量一棵树的高度,在点A处测得树顶C的仰角为 , 在点B处测得树顶C的仰角为 , 且A,B,D三点在同一直线上,若 , 则这棵树的高度是( )
A、 B、 C、 D、4. 如图,某数学兴趣小组测量一棵树的高度,在点A处测得树顶C的仰角为 , 在点B处测得树顶C的仰角为 , 且A,B,D三点在同一直线上,若 , 则这棵树的高度是( )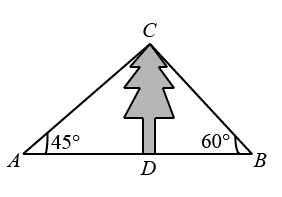 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
5. 一艘轮船位于灯塔的南偏东方向,距离灯塔30海里的处,它沿北偏东方向航行一段时间后,到达位于灯塔的北偏东方向上的处,此时与灯塔的距离约为海里.(参考数据: , , )
 6. 某校数学兴趣小组开展无人机测旗杆的活动:已知无人机的飞行高度为30m,当无人机飞行至A处时,观测旗杆顶部的俯角为30°,继续飞行20m到达B处,测得旗杆顶部的俯角为60°,则旗杆的高度约为m.(参考数据: , 结果按四舍五八保留一位小数)
6. 某校数学兴趣小组开展无人机测旗杆的活动:已知无人机的飞行高度为30m,当无人机飞行至A处时,观测旗杆顶部的俯角为30°,继续飞行20m到达B处,测得旗杆顶部的俯角为60°,则旗杆的高度约为m.(参考数据: , 结果按四舍五八保留一位小数)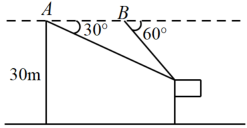 7. 2022年4月16日9时56分,神舟十三号载人飞船返回舱在东风着陆场成功着陆,某一时刻观测点D测得返回舱底部C的仰角∠CDE=45°,降落伞底面圆A点处的仰角∠ADE=46°12′.已知半径OA长14米,拉绳AB长50米,返回舱高度BC为2米,这时返回舱底部离地面的高度CE约为米(精确到米).(参考数据: , , )
7. 2022年4月16日9时56分,神舟十三号载人飞船返回舱在东风着陆场成功着陆,某一时刻观测点D测得返回舱底部C的仰角∠CDE=45°,降落伞底面圆A点处的仰角∠ADE=46°12′.已知半径OA长14米,拉绳AB长50米,返回舱高度BC为2米,这时返回舱底部离地面的高度CE约为米(精确到米).(参考数据: , , )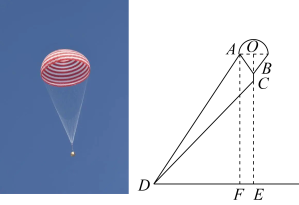 8. 如图,B为地面上一点,测得B到树底部C的距离为 , 在B处放置高的测角仪 , 测得树顶A的仰角为 , 则树高为m(结果保留根号).
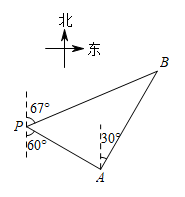
8. 如图,B为地面上一点,测得B到树底部C的距离为 , 在B处放置高的测角仪 , 测得树顶A的仰角为 , 则树高为m(结果保留根号). 9. 如图,测量船以20海里每小时的速度沿正东方向航行并对某海岛进行测量,测量船在A处测得海岛上观测点D位于北偏东15°方向上,观测点C位于北偏东45°方向上,航行半个小时到达B点,这时测得海岛上观测点C位于北偏西45°方向上,若CD与AB平行,则CD=海里(计算结果不取近似值).
9. 如图,测量船以20海里每小时的速度沿正东方向航行并对某海岛进行测量,测量船在A处测得海岛上观测点D位于北偏东15°方向上,观测点C位于北偏东45°方向上,航行半个小时到达B点,这时测得海岛上观测点C位于北偏西45°方向上,若CD与AB平行,则CD=海里(计算结果不取近似值).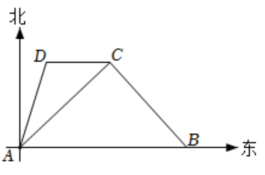 10. 阅读材料:余弦定理是描述三角形中三边长度与一个角余弦值关系的数学定理,运用它可以解决一类已知三角形两边及夹角求第三边或者已知三边求角的问题.余弦定理是这样描述的:在△ABC中,∠A、∠B、∠C所对的边分别为a、b、c,则三角形中任意一边的平方等于另外两边的平方和减去这两边及这两边的夹角的余弦值的乘积的2倍.
10. 阅读材料:余弦定理是描述三角形中三边长度与一个角余弦值关系的数学定理,运用它可以解决一类已知三角形两边及夹角求第三边或者已知三边求角的问题.余弦定理是这样描述的:在△ABC中,∠A、∠B、∠C所对的边分别为a、b、c,则三角形中任意一边的平方等于另外两边的平方和减去这两边及这两边的夹角的余弦值的乘积的2倍.用公式可描述为:a2=b2+c2﹣2bccosA
b2=a2+c2﹣2accosB
c2=a2+b2﹣2abcosC
现已知在△ABC中,AB=3,AC=4,∠A=60°,则BC= .
11. 如图,我海军舰艇在某海域C岛附近巡航,计划从A岛向北偏东80°方向的B岛直线行驶.测得C岛在A岛的北偏东50°方向,在B岛的北偏西40°方向.A,B之间的距离为80nmile,则C岛到航线AB的最短距离是nmile.(参考数据: , , 保留整数结果)
三、解答题
-
12. 如图,湖边、两点由两段笔直的观景栈道和相连.为了计算、两点之间的距离,经测量得: , , 米,求、两点之间的距离.(参考数据: , , , , , )
 13. 如图,公园内有一个垂直于地面的立柱AB,其旁边有一个坡面 , 坡角 . 在阳光下,小明观察到在地面上的影长为 , 在坡面上的影长为 . 同一时刻,小明测得直立于地面长60cm的木杆的影长为90cm(其影子完全落在地面上).求立柱AB的高度.
13. 如图,公园内有一个垂直于地面的立柱AB,其旁边有一个坡面 , 坡角 . 在阳光下,小明观察到在地面上的影长为 , 在坡面上的影长为 . 同一时刻,小明测得直立于地面长60cm的木杆的影长为90cm(其影子完全落在地面上).求立柱AB的高度.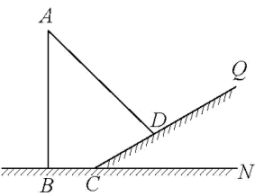 14. 某班同学在一次综合实践课上,测量校园内一棵树的高度.如图,测量仪在A处测得树顶D的仰角为45°,C处测得树顶D的仰角为37°(点A,B,C在一条水平直线上),已知测量仪高度AE=CF=1.6米,AC=28米,求树BD的高度(结果保留小数点后一位.参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75).
14. 某班同学在一次综合实践课上,测量校园内一棵树的高度.如图,测量仪在A处测得树顶D的仰角为45°,C处测得树顶D的仰角为37°(点A,B,C在一条水平直线上),已知测量仪高度AE=CF=1.6米,AC=28米,求树BD的高度(结果保留小数点后一位.参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75). 15. 位于岘山的革命烈士纪念塔是襄阳市的标志性建筑,是为纪念“襄樊战役”中牺牲的革命烈士及第一、第二次国内革命战争时期为襄阳的解放事业献身的革命烈士的而兴建的,某校数学兴趣小组利用无人机测量烈士塔的高度.无人机在点A处测得烈士塔顶部点B的仰角为45°,烈士塔底部点C的俯角为61°,无人机与烈士塔的水平距离AD为10m,求烈士塔的高度.(结果保留整数.参考数据:sin61°≈0.87,cos61°≈0.48,tan61°≈1.80)
15. 位于岘山的革命烈士纪念塔是襄阳市的标志性建筑,是为纪念“襄樊战役”中牺牲的革命烈士及第一、第二次国内革命战争时期为襄阳的解放事业献身的革命烈士的而兴建的,某校数学兴趣小组利用无人机测量烈士塔的高度.无人机在点A处测得烈士塔顶部点B的仰角为45°,烈士塔底部点C的俯角为61°,无人机与烈士塔的水平距离AD为10m,求烈士塔的高度.(结果保留整数.参考数据:sin61°≈0.87,cos61°≈0.48,tan61°≈1.80) 16. 如图,小睿为测量公园的一凉亭AB的高度,他先在水平地面点E处用高1.5m的测角仪DE测得 ,然后沿EB方向向前走3m到达点G处,在点G处用高1.5m的测角仪FG测得 .求凉亭AB的高度.(A,C,B三点共线, , , , .结果精确到0.1m)(参考数据: , , , , , )
16. 如图,小睿为测量公园的一凉亭AB的高度,他先在水平地面点E处用高1.5m的测角仪DE测得 ,然后沿EB方向向前走3m到达点G处,在点G处用高1.5m的测角仪FG测得 .求凉亭AB的高度.(A,C,B三点共线, , , , .结果精确到0.1m)(参考数据: , , , , , ) 17. 为传承运河文明,弘扬民族精神,枣庄市政府重建了台儿庄古城.某校“综合与实践”小组开展了测量台儿庄古城城门楼(如图①)高度的实践活动,请你帮他们完成下面的实践报告.
17. 为传承运河文明,弘扬民族精神,枣庄市政府重建了台儿庄古城.某校“综合与实践”小组开展了测量台儿庄古城城门楼(如图①)高度的实践活动,请你帮他们完成下面的实践报告.测量台儿庄古城城门楼高度的实践报告
活动课题
测量台儿庄古城城门楼高度
活动目的
运用三角函数知识解决实际问题
活动工具
测角仪、皮尺等测量工具
方案示意图
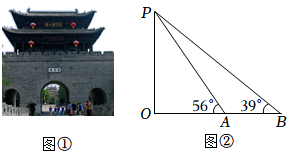
测量步骤
如图②
⑴利用测角仪站在B处测得城门楼最高点P的仰角为39°;
⑵前进了10米到达A处(选择测点A,B与O在同一水平线上,A,B两点之间的距离可直接测得,测角仪高度忽略不计),在A处测得P点的仰角为56°.
参考数据
sin39°≈0.6,cos39°≈0.8,tan39°≈0.8,sin56°≈0.8,cos56°≈0.6,tan56°≈1.5.
计算城门楼PO的高度(结果保留整数)
18. 如图,我国某海域有A,B,C三个港口,B港口在C港口正西方向33.2nmile(nmile是单位“海里”的符号)处,A港口在B港口北偏西50°方向且距离B港口40nmile处,在A港口北偏东53°方向且位于C港口正北方向的点D处有一艘货船,求货船与A港口之间的距离.(参考数据:sin50°≈0.77,cos50°≈0.64,tan50°≈1.19,sin53°≈0.80,cos53°≈0.60,tan53°≈1.33.)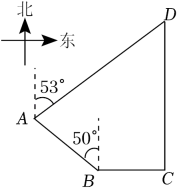 19. 旗杆及升旗台的剖面如图所示,MN、CD为水平线,旗杆AB⊥CD于点B.某一时刻,旗杆AB的一部分影子BD落在CD上,另一部分影子DE落在坡面DN上,已知BD=1.2m,DE=1.4m.同一时刻,测得竖直立在坡面DN上的1m高的标杆影长为0.25m(标杆影子在坡面DN上),此时光线AE与水平线的夹角为80.5°,求旗杆AB的高度.(参考数据:sin80.5°≈0.98,cos80.5°≈0.17,tan80.5°≈6)
19. 旗杆及升旗台的剖面如图所示,MN、CD为水平线,旗杆AB⊥CD于点B.某一时刻,旗杆AB的一部分影子BD落在CD上,另一部分影子DE落在坡面DN上,已知BD=1.2m,DE=1.4m.同一时刻,测得竖直立在坡面DN上的1m高的标杆影长为0.25m(标杆影子在坡面DN上),此时光线AE与水平线的夹角为80.5°,求旗杆AB的高度.(参考数据:sin80.5°≈0.98,cos80.5°≈0.17,tan80.5°≈6) 20. 菏泽某超市计划更换安全性更高的手扶电梯,如图,把电梯坡面的坡角由原来的37°减至30°,已知原电梯坡面AB的长为8米,更换后的电梯坡面为AD,点B延伸至点D,求BD的长.(结果精确到0.1米.参考数据:)
20. 菏泽某超市计划更换安全性更高的手扶电梯,如图,把电梯坡面的坡角由原来的37°减至30°,已知原电梯坡面AB的长为8米,更换后的电梯坡面为AD,点B延伸至点D,求BD的长.(结果精确到0.1米.参考数据:)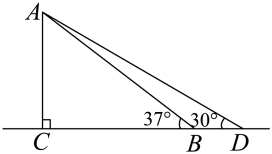 21. 随着我国科学技术的不断发展,科学幻想变为现实.如图1是我国自主研发的某型号隐形战斗机模型,全动型后掠翼垂尾是这款战斗机亮点之一.图2是垂尾模型的轴切面,并通过垂尾模型的外围测得如下数据, , , , , 且 , 求出垂尾模型ABCD的面积.(结果保留整数,参考数据: , )
21. 随着我国科学技术的不断发展,科学幻想变为现实.如图1是我国自主研发的某型号隐形战斗机模型,全动型后掠翼垂尾是这款战斗机亮点之一.图2是垂尾模型的轴切面,并通过垂尾模型的外围测得如下数据, , , , , 且 , 求出垂尾模型ABCD的面积.(结果保留整数,参考数据: , )
图1 图2
22. 如图,小敏在数学实践活动中,利用所学知识对他所在小区居民楼AB的高度进行测量,从小敏家阳台C测得点A的仰角为33°,测得点B的俯角为45°,已知观测点到地面的高度CD=36m,求居民楼AB的高度(结果保留整数.参考数据:sin33°≈0.55,cos33°≈0.84,tan33°≈0.65).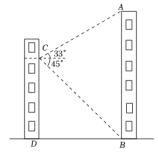 23. 如图是某水库大坝的横截面,坝高 ,背水坡BC的坡度为 .为了对水库大坝进行升级加固,降低背水坡的倾斜程度,设计人员准备把背水坡的坡度改为 ,求背水坡新起点A与原起点B之间的距离.(参考数据: , .结果精确到0.1m)
23. 如图是某水库大坝的横截面,坝高 ,背水坡BC的坡度为 .为了对水库大坝进行升级加固,降低背水坡的倾斜程度,设计人员准备把背水坡的坡度改为 ,求背水坡新起点A与原起点B之间的距离.(参考数据: , .结果精确到0.1m)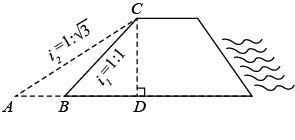 24. 某型号飞机的机翼形状如图所示,根据图中数据计算的长度(结果保留小数点后一位,).
24. 某型号飞机的机翼形状如图所示,根据图中数据计算的长度(结果保留小数点后一位,). 25. 某数学小组要测量学校路灯的顶部到地面的距离,他们借助皮尺、测角仅进行测量,测量结果如下:
25. 某数学小组要测量学校路灯的顶部到地面的距离,他们借助皮尺、测角仅进行测量,测量结果如下:测量项目
测量数据
从A处测得路灯顶部P的仰角
从D处测得路灯顶部P的仰角
测角仪到地面的距离
两次测量时测角仪之间的水平距离
计算路灯顶部到地面的距离约为多少米?(结果精确到0.1米.参考数据;)

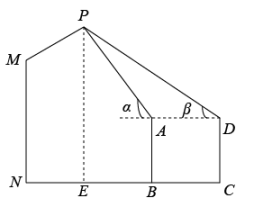 26. 我市某辖区内的兴国寺有一座宋代仿木楼阁式空心砖塔,塔旁有一棵唐代古槐,称为“宋塔唐槐”(如图①).数学兴趣小组利用无人机测量古槐的高度,如图②所示,当无人机从位于塔基B点与古槐底D点之间的地面H点,竖直起飞到正上方45米E点处时,测得塔AB的顶端A和古槐CD的顶端C的俯角分别为26.6°和76°(点B,H,D三点在同一直线上).已知塔高为39米,塔基B与树底D的水平距离为20米,求古槐的高度(结果精确到1米).(参考数据: , , , , , )
26. 我市某辖区内的兴国寺有一座宋代仿木楼阁式空心砖塔,塔旁有一棵唐代古槐,称为“宋塔唐槐”(如图①).数学兴趣小组利用无人机测量古槐的高度,如图②所示,当无人机从位于塔基B点与古槐底D点之间的地面H点,竖直起飞到正上方45米E点处时,测得塔AB的顶端A和古槐CD的顶端C的俯角分别为26.6°和76°(点B,H,D三点在同一直线上).已知塔高为39米,塔基B与树底D的水平距离为20米,求古槐的高度(结果精确到1米).(参考数据: , , , , , ) 27. 北京时间2022年4月16日9时56分,神舟十三号载人飞船返回舱成功着陆.为弘扬航天精神,某校在教学楼上悬挂了一幅长为的励志条幅(即).小亮同学想知道条幅的底端到地面的距离,他的测量过程如下:如图,首先他站在楼前点处,在点正上方点处测得条幅顶端的仰角为 , 然后向教学楼条幅方向前行到达点处(楼底部点与点 , 在一条直线上),在点正上方点处测得条幅底端的仰角为 , 若 , 均为(即四边形为矩形),请你帮助小亮计算条幅底端到地面的距离的长度.(结果精确到 , 参考数据: , , )
27. 北京时间2022年4月16日9时56分,神舟十三号载人飞船返回舱成功着陆.为弘扬航天精神,某校在教学楼上悬挂了一幅长为的励志条幅(即).小亮同学想知道条幅的底端到地面的距离,他的测量过程如下:如图,首先他站在楼前点处,在点正上方点处测得条幅顶端的仰角为 , 然后向教学楼条幅方向前行到达点处(楼底部点与点 , 在一条直线上),在点正上方点处测得条幅底端的仰角为 , 若 , 均为(即四边形为矩形),请你帮助小亮计算条幅底端到地面的距离的长度.(结果精确到 , 参考数据: , , )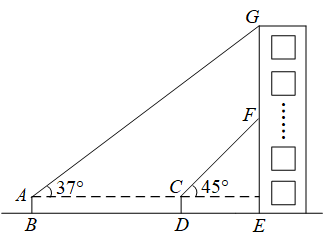 28. 如图,一艘货轮在海面上航行,准备要停靠到码头C,货轮航行到A处时,测得码头C在北偏东60°方向上.为了躲避A,C之间的暗礁,这艘货轮调整航向,沿着北偏东30°方向继续航行,当它航行到B处后,又沿着南偏东70°方向航行20海里到达码头C.求货轮从A到B航行的距离(结果精确到0.1海里.参考数据:sin50°≈0.766,cos50°≈0.643,tan50°≈1.192).
28. 如图,一艘货轮在海面上航行,准备要停靠到码头C,货轮航行到A处时,测得码头C在北偏东60°方向上.为了躲避A,C之间的暗礁,这艘货轮调整航向,沿着北偏东30°方向继续航行,当它航行到B处后,又沿着南偏东70°方向航行20海里到达码头C.求货轮从A到B航行的距离(结果精确到0.1海里.参考数据:sin50°≈0.766,cos50°≈0.643,tan50°≈1.192).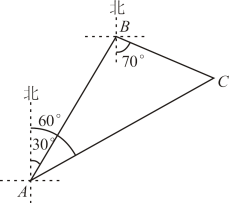 29. 胜利黄河大桥犹如一架巨大的竖琴,凌驾于滔滔黄河之上,使黄河南北“天堑变通途”.已知主塔垂直于桥面于点B,其中两条斜拉索与桥面的夹角分别为和 , 两固定点D、C之间的距离约为 , 求主塔的高度(结果保留整数,参考数据:)
29. 胜利黄河大桥犹如一架巨大的竖琴,凌驾于滔滔黄河之上,使黄河南北“天堑变通途”.已知主塔垂直于桥面于点B,其中两条斜拉索与桥面的夹角分别为和 , 两固定点D、C之间的距离约为 , 求主塔的高度(结果保留整数,参考数据:) 30. 八年级二班学生到某劳动教育实践基地开展实践活动,当天,他们先从基地门口A处向正北方向走了450米,到达菜园B处锄草,再从B处沿正西方向到达果园C处采摘水果,再向南偏东37°方向走了300米,到达手工坊D处进行手工制作,最后从D处回到门口A处,手工坊在基地门口北偏西65°方向上.求菜园与果园之间的距离.(结果保留整数)参考数据:sin65°≈ 0.91,cos65°≈0.42,tan65°≈2.14,sin37°≈ 0.60,cos37°≈ 0.80,tan37°≈0.75
30. 八年级二班学生到某劳动教育实践基地开展实践活动,当天,他们先从基地门口A处向正北方向走了450米,到达菜园B处锄草,再从B处沿正西方向到达果园C处采摘水果,再向南偏东37°方向走了300米,到达手工坊D处进行手工制作,最后从D处回到门口A处,手工坊在基地门口北偏西65°方向上.求菜园与果园之间的距离.(结果保留整数)参考数据:sin65°≈ 0.91,cos65°≈0.42,tan65°≈2.14,sin37°≈ 0.60,cos37°≈ 0.80,tan37°≈0.75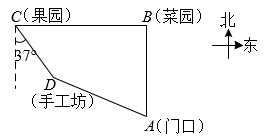
四、综合题
-
31. 小明学了《解直角三角形》内容后,对一条东西走向的隧道进行实地测量.如图所示,他在地面上点C处测得隧道一端点A在他的北偏东方向上,他沿西北方向前进米后到达点D,此时测得点A在他的东北方向上,端点B在他的北偏西方向上,(点A、B、C、D在同一平面内)
 (1)、求点D与点A的距离;(2)、求隧道的长度.(结果保留根号)32. 随着我国科学技术的不断发展,5G移动通信技术日趋完善.某市政府为了实现5G网络全覆盖,2021~2025年拟建设5G基站3000个,如图,在斜坡上有一建成的5G基站塔 , 小明在坡脚处测得塔顶的仰角为 , 然后他沿坡面行走了50米到达处,处离地平面的距离为30米且在处测得塔顶的仰角 . (点、、、、均在同一平面内,为地平线)(参考数据: , , )
(1)、求点D与点A的距离;(2)、求隧道的长度.(结果保留根号)32. 随着我国科学技术的不断发展,5G移动通信技术日趋完善.某市政府为了实现5G网络全覆盖,2021~2025年拟建设5G基站3000个,如图,在斜坡上有一建成的5G基站塔 , 小明在坡脚处测得塔顶的仰角为 , 然后他沿坡面行走了50米到达处,处离地平面的距离为30米且在处测得塔顶的仰角 . (点、、、、均在同一平面内,为地平线)(参考数据: , , ) (1)、求坡面的坡度;(2)、求基站塔的高.33. 2022年北京冬奥会的成功举办激发了人们对冰雪运动的热情.如图是某滑雪场的横截面示意图,雪道分为AB,BC两部分,小明同学在C点测得雪道BC的坡度i=1:2.4,在A点测得B点的俯角∠DAB=30°.若雪道AB长为270m,雪道BC长为260m.
(1)、求坡面的坡度;(2)、求基站塔的高.33. 2022年北京冬奥会的成功举办激发了人们对冰雪运动的热情.如图是某滑雪场的横截面示意图,雪道分为AB,BC两部分,小明同学在C点测得雪道BC的坡度i=1:2.4,在A点测得B点的俯角∠DAB=30°.若雪道AB长为270m,雪道BC长为260m.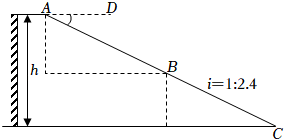 (1)、求该滑雪场的高度h;(2)、据了解,该滑雪场要用两种不同的造雪设备来满足对于雪量和雪质的不同要求,其中甲设备每小时造雪量比乙设备少35m3 , 且甲设备造雪150m3所用的时间与乙设备造雪500m3所用的时间相等.求甲、乙两种设备每小时的造雪量.34. 知识再现:如图1,在Rt△ABC中,∠C=90°,∠A,∠B,∠C的对边分别为a,b,c.
(1)、求该滑雪场的高度h;(2)、据了解,该滑雪场要用两种不同的造雪设备来满足对于雪量和雪质的不同要求,其中甲设备每小时造雪量比乙设备少35m3 , 且甲设备造雪150m3所用的时间与乙设备造雪500m3所用的时间相等.求甲、乙两种设备每小时的造雪量.34. 知识再现:如图1,在Rt△ABC中,∠C=90°,∠A,∠B,∠C的对边分别为a,b,c.∵ ,
∴ ,
∴
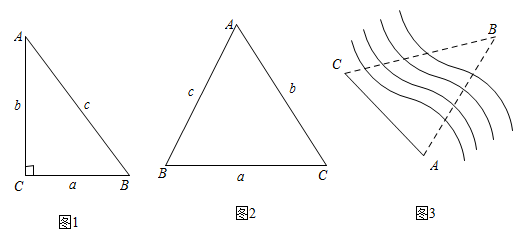 (1)、拓展探究:如图2,在锐角ABC中,∠A,∠B,∠C的对边分别为a,b,c.请探究 , , 之间的关系,并写出探究过程.(2)、解决问题:如图3,为测量点A到河对岸点B的距离,选取与点A在河岸同一侧的点C,测得AC=60m,∠A=75°,∠C=60°.请用拓展探究中的结论,求点A到点B的距离.35. 2022年6月5日,“神舟十四号”载人航天飞船搭载“明星”机械臂成功发射.如图是处于工作状态的某型号手臂机器人示意图,是垂直于工作台的移动基座,、为机械臂,m,m,m, . 机械臂端点到工作台的距离m.
(1)、拓展探究:如图2,在锐角ABC中,∠A,∠B,∠C的对边分别为a,b,c.请探究 , , 之间的关系,并写出探究过程.(2)、解决问题:如图3,为测量点A到河对岸点B的距离,选取与点A在河岸同一侧的点C,测得AC=60m,∠A=75°,∠C=60°.请用拓展探究中的结论,求点A到点B的距离.35. 2022年6月5日,“神舟十四号”载人航天飞船搭载“明星”机械臂成功发射.如图是处于工作状态的某型号手臂机器人示意图,是垂直于工作台的移动基座,、为机械臂,m,m,m, . 机械臂端点到工作台的距离m.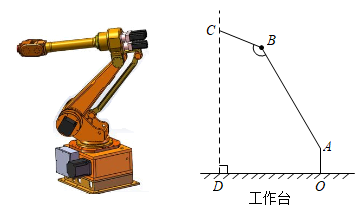 (1)、求、两点之间的距离;(2)、求长.(结果精确到0.1m,参考数据: , , , )36. 如图,莲花山是大连著名的景点之一,游客可以从山底乘坐索道车到达山项,索速车运行的速度是1米/秒,小明要测量莲花山山顶白塔的高度,他在索道A处测得白塔底部B的仰角的为 , 测得白塔顶部C的仰角的为 . 索道车从A处运行到B处所用时间的为5分钟.
(1)、求、两点之间的距离;(2)、求长.(结果精确到0.1m,参考数据: , , , )36. 如图,莲花山是大连著名的景点之一,游客可以从山底乘坐索道车到达山项,索速车运行的速度是1米/秒,小明要测量莲花山山顶白塔的高度,他在索道A处测得白塔底部B的仰角的为 , 测得白塔顶部C的仰角的为 . 索道车从A处运行到B处所用时间的为5分钟. (1)、索道车从A处运行到B处的距离约为米;(2)、请你利用小明测量的数据,求白塔的高度(结果取整数).(参考数据:)37. 某数学活动小组利用太阳光线下物体的影子和标杆测量旗杆的高度.如图,在某一时刻,旗杆的AB的影子为BC,与此同时在C处立一根标杆CD,标杆CD的影子为CE, CD = 1.6m,BC =5CD.
(1)、索道车从A处运行到B处的距离约为米;(2)、请你利用小明测量的数据,求白塔的高度(结果取整数).(参考数据:)37. 某数学活动小组利用太阳光线下物体的影子和标杆测量旗杆的高度.如图,在某一时刻,旗杆的AB的影子为BC,与此同时在C处立一根标杆CD,标杆CD的影子为CE, CD = 1.6m,BC =5CD.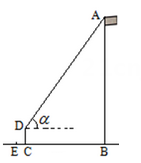 (1)、求BC的长;(2)、从条件①、条件②这两个条件中选择一个作为已知,
(1)、求BC的长;(2)、从条件①、条件②这两个条件中选择一个作为已知,求旗杆AB的高度.
条件①:CE = 1.0m; 条件②:从D处看旗杆顶部A的仰角为54.46°.
注:如果选择条件①和条件②分别作答,按第一个解答计分.参考数据:sin54.46°≈0.81, cos54.46°≈0.58, tan54.46°≈1.40 .
38. 我们经常会采用不同方法对某物体进行测量,请测量下列灯杆AB的长. (1)、如图1所示,将一个测角仪放置在距离灯杆AB底部a米的点D处,测角仪高为b米,从C点测得A点的仰角为α,求灯杆AB的高度.(用含a,b,a的代数式表示)(2)、我国古代数学家赵爽利用影子对物体进行测量的方法,在至今仍有借鉴意义图2所示,现将一高度为2米的木杆CG放在灯杆AB前,测得其影长CH为1米,再将木杆沿着BC方向移动1.8米至DE的位置,此时测得其影长DF为3米,求灯杆AB的高度39. 某数学兴趣小组准备测量校园内旗杆顶端到地面的高度(旗杆底端有台阶).该小组在C处安置测角仪CD,测得旗杆顶端A的仰角为30°,前进8m到达E处,安置测角仪EF,测得旗杆顶端A的仰角为45°(点B,E,C在同一直线上),测角仪支架高CD=EF=1.2m,求旗杆顶端A到地面的距离即AB的长度.(结果精确到1m.参考数据:≈1.7)
(1)、如图1所示,将一个测角仪放置在距离灯杆AB底部a米的点D处,测角仪高为b米,从C点测得A点的仰角为α,求灯杆AB的高度.(用含a,b,a的代数式表示)(2)、我国古代数学家赵爽利用影子对物体进行测量的方法,在至今仍有借鉴意义图2所示,现将一高度为2米的木杆CG放在灯杆AB前,测得其影长CH为1米,再将木杆沿着BC方向移动1.8米至DE的位置,此时测得其影长DF为3米,求灯杆AB的高度39. 某数学兴趣小组准备测量校园内旗杆顶端到地面的高度(旗杆底端有台阶).该小组在C处安置测角仪CD,测得旗杆顶端A的仰角为30°,前进8m到达E处,安置测角仪EF,测得旗杆顶端A的仰角为45°(点B,E,C在同一直线上),测角仪支架高CD=EF=1.2m,求旗杆顶端A到地面的距离即AB的长度.(结果精确到1m.参考数据:≈1.7)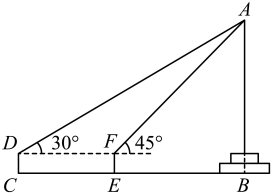 40. 交通安全心系千万家.高速公路管理局在某隧道内安装了测速仪,如图所示的是该段隧道的截面示意图.测速仪和测速仪到路面之间的距离 , 测速仪和之间的距离 , 一辆小汽车在水平的公路上由西向东匀速行驶,在测速仪处测得小汽车在隧道入口点的俯角为25°,在测速仪处测得小汽车在点的俯角为60°,小汽车在隧道中从点行驶到点所用的时间为38s(图中所有点都在同一平面内).
40. 交通安全心系千万家.高速公路管理局在某隧道内安装了测速仪,如图所示的是该段隧道的截面示意图.测速仪和测速仪到路面之间的距离 , 测速仪和之间的距离 , 一辆小汽车在水平的公路上由西向东匀速行驶,在测速仪处测得小汽车在隧道入口点的俯角为25°,在测速仪处测得小汽车在点的俯角为60°,小汽车在隧道中从点行驶到点所用的时间为38s(图中所有点都在同一平面内).
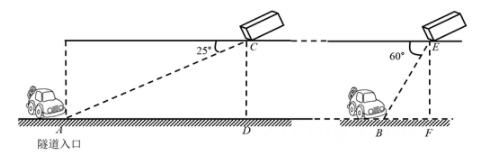 (1)、求 , 两点之间的距离(结果精确到1m);(2)、若该隧道限速22m/s,判断小汽车从点行驶到点是否超速?通过计算说明理由.(参考数据: , , , , , )
(1)、求 , 两点之间的距离(结果精确到1m);(2)、若该隧道限速22m/s,判断小汽车从点行驶到点是否超速?通过计算说明理由.(参考数据: , , , , , )