2022年全国中考数学真题分类汇编20 圆(5)
试卷更新日期:2022-12-29 类型:二轮复习
一、单选题
-
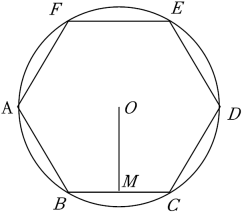
1. 如图,正六边形ABCDEF内接于⊙O,半径为6,则这个正六边形的边心距OM和的长分别为( )
 A、4, B、3 , π C、2 , D、3 , 2π2. 如图,在等腰直角 中,点E在OA上,以点O为圆心、OE为半径作圆弧交OB于点F,连接EF,已知阴影部分面积为 ,则EF的长度为( )
A、4, B、3 , π C、2 , D、3 , 2π2. 如图,在等腰直角 中,点E在OA上,以点O为圆心、OE为半径作圆弧交OB于点F,连接EF,已知阴影部分面积为 ,则EF的长度为( )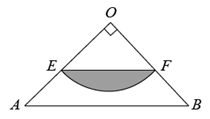 A、 B、2 C、 D、3. 如图,在 中, ,将 绕点A逆时针旋转 ,得到 ,连接 并延长交AB于点D,当 时, 的长是( )
A、 B、2 C、 D、3. 如图,在 中, ,将 绕点A逆时针旋转 ,得到 ,连接 并延长交AB于点D,当 时, 的长是( )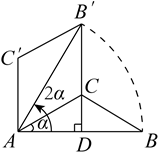 A、 B、 C、 D、4. 如图,一件扇形艺术品完全打开后,夹角为 , 的长为 , 扇面的长为 , 则扇面的面积是( )
A、 B、 C、 D、4. 如图,一件扇形艺术品完全打开后,夹角为 , 的长为 , 扇面的长为 , 则扇面的面积是( )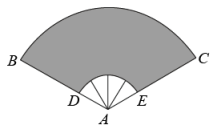 A、375πcm2 B、450πcm2 C、600πcm2 D、750πcm25. 如图,PA,PB是的切线,A、B为切点,若 , 则的度数为( )
A、375πcm2 B、450πcm2 C、600πcm2 D、750πcm25. 如图,PA,PB是的切线,A、B为切点,若 , 则的度数为( )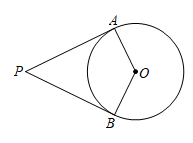 A、 B、 C、 D、6. 如图,已知正六边形内接于半径为的 , 随机地往内投一粒米,落在正六边形内的概率为( )
A、 B、 C、 D、6. 如图,已知正六边形内接于半径为的 , 随机地往内投一粒米,落在正六边形内的概率为( )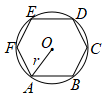 A、 B、 C、 D、以上答案都不对7. 如图,、分别与相切于点、 , 连接并延长与交于点、 , 若 , , 则的值为( )
A、 B、 C、 D、以上答案都不对7. 如图,、分别与相切于点、 , 连接并延长与交于点、 , 若 , , 则的值为( ) A、 B、 C、 D、8. 工人师傅为检测该厂生产的一种铁球的大小是否符合要求,设计了一个如图(1)所示的工件槽,其两个底角均为90°,将形状规则的铁球放入槽内时,若同时具有图(1)所示的A、B、E三个接触点,该球的大小就符合要求.图(2)是过球心及A、B、E三点的截面示意图,已知⊙O的直径就是铁球的直径,AB是⊙O的弦,CD切⊙O于点E,AC⊥CD、BD⊥CD,若CD=16cm,AC=BD=4cm,则这种铁球的直径为( )
A、 B、 C、 D、8. 工人师傅为检测该厂生产的一种铁球的大小是否符合要求,设计了一个如图(1)所示的工件槽,其两个底角均为90°,将形状规则的铁球放入槽内时,若同时具有图(1)所示的A、B、E三个接触点,该球的大小就符合要求.图(2)是过球心及A、B、E三点的截面示意图,已知⊙O的直径就是铁球的直径,AB是⊙O的弦,CD切⊙O于点E,AC⊥CD、BD⊥CD,若CD=16cm,AC=BD=4cm,则这种铁球的直径为( ) A、10cm B、15cm C、20cm D、24cm9. 如图, 是等边 的外接圆,点 是弧 上一动点(不与 , 重合),下列结论:① ;② ;③当 最长时, ;④ ,其中一定正确的结论有( )
A、10cm B、15cm C、20cm D、24cm9. 如图, 是等边 的外接圆,点 是弧 上一动点(不与 , 重合),下列结论:① ;② ;③当 最长时, ;④ ,其中一定正确的结论有( )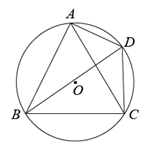 A、1个 B、2个 C、3个 D、4个10. 如图,以边长为2的等边△ABC顶点A为圆心、一定的长为半径画弧,恰好与BC边相切,分别交AB,AC于D,E,则图中阴影部分的面积是( )
A、1个 B、2个 C、3个 D、4个10. 如图,以边长为2的等边△ABC顶点A为圆心、一定的长为半径画弧,恰好与BC边相切,分别交AB,AC于D,E,则图中阴影部分的面积是( )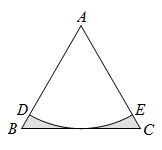 A、 B、 C、 D、11. 如图,的重心为 , 的中点为 , 今以为圆心,长为半径画一圆,且作点到圆的两切线段、 , 其中、均为切点.根据图中标示的角与角度,求与的度数和为多少?( )
A、 B、 C、 D、11. 如图,的重心为 , 的中点为 , 今以为圆心,长为半径画一圆,且作点到圆的两切线段、 , 其中、均为切点.根据图中标示的角与角度,求与的度数和为多少?( ) A、30 B、35 C、40 D、45
A、30 B、35 C、40 D、45二、填空题
-
12. 如图,射线AB与⊙O相切于点B,经过圆心O的射线AC与⊙O相交于点D、C,连接BC,若∠A=40°,则∠ACB=.
 13. 如图,A、B、C是上的点, , 垂足为点D,且D为OC的中点,若 , 则BC的长为.
13. 如图,A、B、C是上的点, , 垂足为点D,且D为OC的中点,若 , 则BC的长为. 14. 如图,在中, , 半径为3cm的是的内切圆,连接、 , 则图中阴影部分的面积是cm2.(结果用含的式子表示)
14. 如图,在中, , 半径为3cm的是的内切圆,连接、 , 则图中阴影部分的面积是cm2.(结果用含的式子表示)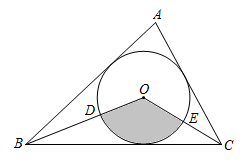 15. 如图,在中,为直径, , 为弦,过点的切线与的延长线交于点 , 为线段上一点(不与点重合),且.
15. 如图,在中,为直径, , 为弦,过点的切线与的延长线交于点 , 为线段上一点(不与点重合),且.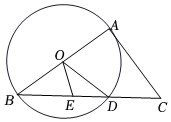 (1)、若 , 则的长为(结果保留);(2)、若 , 则.16. 如图,在中,AB是的弦,的半径为3cm,C为上一点, , 则AB的长为cm.
(1)、若 , 则的长为(结果保留);(2)、若 , 则.16. 如图,在中,AB是的弦,的半径为3cm,C为上一点, , 则AB的长为cm. 17. 已知圆锥的高为8cm,母线长为10cm,则其侧面展开图的面积为 .18. 若一个圆锥的母线长为5cm,它的侧面展开图的圆心角为120°,则这个圆锥的底面半径为cm.19. 扇形的半径为2,圆心角为90°,则该扇形的面积(结果保留 )为 .20. 如图,将一个球放置在圆柱形玻璃瓶上,测得瓶高AB=20cm,底面直径BC=12cm,球的最高点到瓶底面的距离为32cm,则球的半径为cm(玻璃瓶厚度忽略不计).
17. 已知圆锥的高为8cm,母线长为10cm,则其侧面展开图的面积为 .18. 若一个圆锥的母线长为5cm,它的侧面展开图的圆心角为120°,则这个圆锥的底面半径为cm.19. 扇形的半径为2,圆心角为90°,则该扇形的面积(结果保留 )为 .20. 如图,将一个球放置在圆柱形玻璃瓶上,测得瓶高AB=20cm,底面直径BC=12cm,球的最高点到瓶底面的距离为32cm,则球的半径为cm(玻璃瓶厚度忽略不计). 21. 如图,将扇形AOB沿OB方向平移,使点O移到OB的中点 处,得到扇形 .若∠O=90°,OA=2,则阴影部分的面积为.
21. 如图,将扇形AOB沿OB方向平移,使点O移到OB的中点 处,得到扇形 .若∠O=90°,OA=2,则阴影部分的面积为. 22. 我国古代数学家赵爽的“弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形(如图所示).若直角三角形的内切圆半径为3,小正方形的面积为49,则大正方形的面积为.
22. 我国古代数学家赵爽的“弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形(如图所示).若直角三角形的内切圆半径为3,小正方形的面积为49,则大正方形的面积为. 23. 如图,是的直径,点、在上, , 则度.
23. 如图,是的直径,点、在上, , 则度. 24. 如图,在中, , , , 半径为1的在内平移(可以与该三角形的边相切),则点到上的点的距离的最大值为.
24. 如图,在中, , , , 半径为1的在内平移(可以与该三角形的边相切),则点到上的点的距离的最大值为.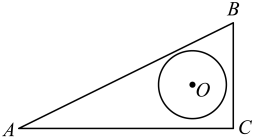
三、综合题
-
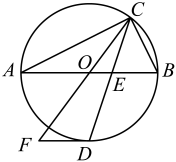
25. 如图, 内接于 ,AB是直径,延长AB到点E,使得 ,连接EC,且 ,点D是 上的点,连接AD,CD,且CD交AB于点F.
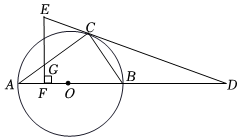
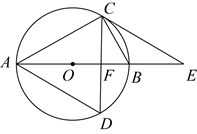 (1)、求证:EC是 的切线;(2)、若BC平分 ,求AD的长.26. 如图,在 中, ,以AC为直径作 交BC于点D,过点D作 ,垂足为E,延长BA交 于点F.
(1)、求证:EC是 的切线;(2)、若BC平分 ,求AD的长.26. 如图,在 中, ,以AC为直径作 交BC于点D,过点D作 ,垂足为E,延长BA交 于点F.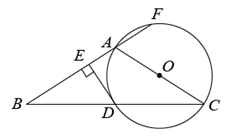 (1)、求证:DE是 的切线(2)、若 ,求 的半径.27.(1)、请在图中作出的外接圆(尺规作图,保留作图痕迹,不写作法);
(1)、求证:DE是 的切线(2)、若 ,求 的半径.27.(1)、请在图中作出的外接圆(尺规作图,保留作图痕迹,不写作法);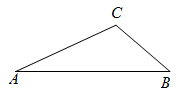 (2)、如图,是的外接圆,是的直径,点是的中点,过点的切线与的延长线交于点.
(2)、如图,是的外接圆,是的直径,点是的中点,过点的切线与的延长线交于点.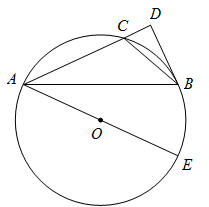
①求证:;
②若 , , 求的半径.
28. 如图,四边形ABCD内接于 , 对角线AC,BD相交于点E,点F在边AD上,连接EF.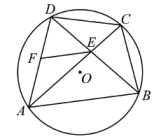 (1)、求证:;(2)、当时,则;;.(直接将结果填写在相应的横线上)(3)、①记四边形ABCD,的面积依次为 , 若满足 , 试判断,的形状,并说明理由.
(1)、求证:;(2)、当时,则;;.(直接将结果填写在相应的横线上)(3)、①记四边形ABCD,的面积依次为 , 若满足 , 试判断,的形状,并说明理由.②当 , 时,试用含m,n,p的式子表示.
29. 如图,△ABC内接于⊙O,交⊙O于点D,交BC于点E,交⊙O于点F,连接AF,CF.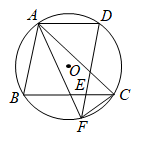 (1)、求证:AC=AF;(2)、若⊙O的半径为3,∠CAF=30°,求的长(结果保留π).30. 如图,在中, , D是边上一点,以为直径的与相切于点E,连接并延长交的延长线于点F.
(1)、求证:AC=AF;(2)、若⊙O的半径为3,∠CAF=30°,求的长(结果保留π).30. 如图,在中, , D是边上一点,以为直径的与相切于点E,连接并延长交的延长线于点F. (1)、求证:;(2)、若 , 求直径.31. 如图,△ABC内接于⊙O,P是⊙O的直径AB延长线上一点,∠PCB=∠OAC,过点O作BC的平行线交PC的延长线于点D.
(1)、求证:;(2)、若 , 求直径.31. 如图,△ABC内接于⊙O,P是⊙O的直径AB延长线上一点,∠PCB=∠OAC,过点O作BC的平行线交PC的延长线于点D.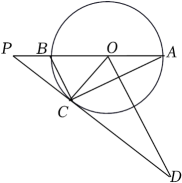 (1)、试判断PC与⊙O的位置关系,并说明理由;(2)、若PC=4,tanA= , 求△OCD的面积.32. 如图,四边形ABCD是⊙O的内接四边形,连接AC,BD,延长CD至点E.
(1)、试判断PC与⊙O的位置关系,并说明理由;(2)、若PC=4,tanA= , 求△OCD的面积.32. 如图,四边形ABCD是⊙O的内接四边形,连接AC,BD,延长CD至点E.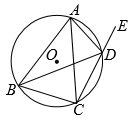 (1)、若AB=AC,求证:∠ADB=∠ADE;(2)、若BC=3,⊙O的半径为2,求sin∠BAC.33. 如图所示,在的内接中, , , 作于点P,交于另一点B,C是上的一个动点(不与A,M重合),射线交线段的延长线于点D,分别连接和 , 交于点E.
(1)、若AB=AC,求证:∠ADB=∠ADE;(2)、若BC=3,⊙O的半径为2,求sin∠BAC.33. 如图所示,在的内接中, , , 作于点P,交于另一点B,C是上的一个动点(不与A,M重合),射线交线段的延长线于点D,分别连接和 , 交于点E. (1)、求证: .(2)、若 , , 求的长.(3)、在点C运动过程中,当时,求的值.34. 如图,在△ABC中,AB=AC,以AB为直径作⊙O,AC与⊙O交于点D,BC与⊙O交于点E,过点C作 , 且CF=CD,连接BF.
(1)、求证: .(2)、若 , , 求的长.(3)、在点C运动过程中,当时,求的值.34. 如图,在△ABC中,AB=AC,以AB为直径作⊙O,AC与⊙O交于点D,BC与⊙O交于点E,过点C作 , 且CF=CD,连接BF.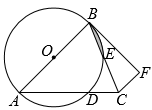 (1)、求证:BF是⊙O的切线;(2)、若∠BAC=45°,AD=4,求图中阴影部分的面积.35. 如图, 中, , 为 上一点,以 为直径的 与 相切于点 ,交 于点 , ,垂足为 .
(1)、求证:BF是⊙O的切线;(2)、若∠BAC=45°,AD=4,求图中阴影部分的面积.35. 如图, 中, , 为 上一点,以 为直径的 与 相切于点 ,交 于点 , ,垂足为 . (1)、求证: 是 的切线;(2)、若 , ,求 的长.36. 如图1,在矩形ABCD中,AB=4,AD=3,点O是边AB上一个动点(不与点A重合),连接OD,将△OAD沿OD折叠,得到△OED;再以O为圆心,OA的长为半径作半圆,交射线AB于G,连接AE并延长交射线BC于F,连接EG,设OA=x.
(1)、求证: 是 的切线;(2)、若 , ,求 的长.36. 如图1,在矩形ABCD中,AB=4,AD=3,点O是边AB上一个动点(不与点A重合),连接OD,将△OAD沿OD折叠,得到△OED;再以O为圆心,OA的长为半径作半圆,交射线AB于G,连接AE并延长交射线BC于F,连接EG,设OA=x.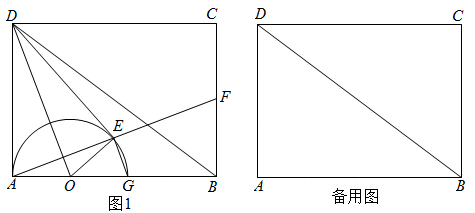 (1)、求证:DE是半圆O的切线;(2)、当点E落在BD上时,求x的值;(3)、当点E落在BD下方时,设△AGE与△AFB面积的比值为y,确定y与x之间的函数关系式;(4)、直接写出:当半圆O与△BCD的边有两个交点时,x的取值范围.37. 为弘扬民族传统体育文化,某校将传统游戏“滚铁环”列入了校运动会的比赛项目.滚铁环器材由铁环和推杆组成.小明对滚铁环的启动阶段进行了研究,如图,滚铁环时,铁环⊙O与水平地面相切于点C,推杆AB与铅垂线AD的夹角为∠BAD,点O,A,B,C,D在同一平面内.当推杆AB与铁环⊙O相切于点B时,手上的力量通过切点B传递到铁环上,会有较好的启动效果.
(1)、求证:DE是半圆O的切线;(2)、当点E落在BD上时,求x的值;(3)、当点E落在BD下方时,设△AGE与△AFB面积的比值为y,确定y与x之间的函数关系式;(4)、直接写出:当半圆O与△BCD的边有两个交点时,x的取值范围.37. 为弘扬民族传统体育文化,某校将传统游戏“滚铁环”列入了校运动会的比赛项目.滚铁环器材由铁环和推杆组成.小明对滚铁环的启动阶段进行了研究,如图,滚铁环时,铁环⊙O与水平地面相切于点C,推杆AB与铅垂线AD的夹角为∠BAD,点O,A,B,C,D在同一平面内.当推杆AB与铁环⊙O相切于点B时,手上的力量通过切点B传递到铁环上,会有较好的启动效果.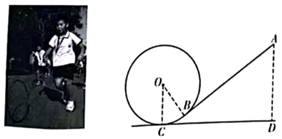 (1)、求证:∠BOC+∠BAD=90°.(2)、实践中发现,切点B只有在铁环上一定区域内时,才能保证铁环平稳启动.图中点B是该区域内最低位置,此时点A距地面的距离AD最小,测得 .已知铁环⊙O的半经为25cm,推杆AB的长为75cm,求此时AD的长.
(1)、求证:∠BOC+∠BAD=90°.(2)、实践中发现,切点B只有在铁环上一定区域内时,才能保证铁环平稳启动.图中点B是该区域内最低位置,此时点A距地面的距离AD最小,测得 .已知铁环⊙O的半经为25cm,推杆AB的长为75cm,求此时AD的长.