2022年全国中考数学真题分类汇编20 圆(4)
试卷更新日期:2022-12-29 类型:二轮复习
一、单选题
-
1. 如图,在矩形中, , , 以点为圆心,长为半径画弧,交于点 , 连接 , 则扇形的面积为( )
 A、 B、 C、 D、2. 用一张半圆形铁皮,围成一个底面半径为的圆锥形工件的侧面(接缝忽略不计),则圆锥的母线长为( )A、 B、 C、 D、3. 蒙古包可以近似地看作由圆锥和圆柱组成.下图是一个蒙古包的示意图,底面圆半径DE=2m,圆锥的高AC=1.5m,圆柱的高CD=2.5m,则下列说法错误的是( )
A、 B、 C、 D、2. 用一张半圆形铁皮,围成一个底面半径为的圆锥形工件的侧面(接缝忽略不计),则圆锥的母线长为( )A、 B、 C、 D、3. 蒙古包可以近似地看作由圆锥和圆柱组成.下图是一个蒙古包的示意图,底面圆半径DE=2m,圆锥的高AC=1.5m,圆柱的高CD=2.5m,则下列说法错误的是( ) A、圆柱的底面积为4πm2 B、圆柱的侧面积为10πm2 C、圆锥的母线AB长为2.25m D、圆锥的侧面积为5πm24. 如图,是的两条半径,点C在上,若 , 则的度数为( )
A、圆柱的底面积为4πm2 B、圆柱的侧面积为10πm2 C、圆锥的母线AB长为2.25m D、圆锥的侧面积为5πm24. 如图,是的两条半径,点C在上,若 , 则的度数为( ) A、 B、 C、 D、5. 一个扇形的弧长是 , 其圆心角是150°,此扇形的面积为( )A、 B、 C、 D、6. 如图,已知⊙O的周长等于6π,则该圆内接正六边形ABCDEF的边心距OG为( )
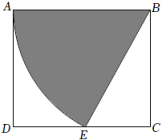
A、 B、 C、 D、5. 一个扇形的弧长是 , 其圆心角是150°,此扇形的面积为( )A、 B、 C、 D、6. 如图,已知⊙O的周长等于6π,则该圆内接正六边形ABCDEF的边心距OG为( )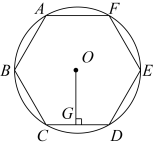 A、3 B、 C、 D、37. 如图,在正方形中,和交于点O,过点O的直线交于点(E不与A,B重合),交于点F.以点O为圆心,为半径的圆交直线于点M,N.若 , 则图中阴影部分的面积为( )
A、3 B、 C、 D、37. 如图,在正方形中,和交于点O,过点O的直线交于点(E不与A,B重合),交于点F.以点O为圆心,为半径的圆交直线于点M,N.若 , 则图中阴影部分的面积为( )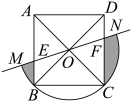 EA、 B、 C、 D、8. 如图,是的直径,点P在的延长线上,与相切于点A,连接 , 若 , 则的度数为( )
EA、 B、 C、 D、8. 如图,是的直径,点P在的延长线上,与相切于点A,连接 , 若 , 则的度数为( ) A、 B、 C、 D、9. 如图,在中, , , . 以点为圆心,为半径作圆,当点在内且点在外时,的值可能是( )
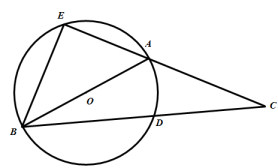
A、 B、 C、 D、9. 如图,在中, , , . 以点为圆心,为半径作圆,当点在内且点在外时,的值可能是( )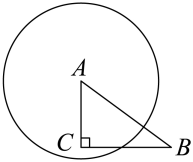 A、2 B、3 C、4 D、510. 如图的电子装置中,红黑两枚跳棋开始放置在边长为2的正六边形 的顶点A处.两枚跳棋跳动规则是:红跳棋按顺时针方向1秒钟跳1个顶点,黑跳棋按逆时针方向3秒钟跳1个顶点,两枚跳棋同时跳动,经过2022秒钟后,两枚跳棋之间的距离是( )
A、2 B、3 C、4 D、510. 如图的电子装置中,红黑两枚跳棋开始放置在边长为2的正六边形 的顶点A处.两枚跳棋跳动规则是:红跳棋按顺时针方向1秒钟跳1个顶点,黑跳棋按逆时针方向3秒钟跳1个顶点,两枚跳棋同时跳动,经过2022秒钟后,两枚跳棋之间的距离是( )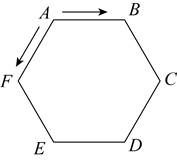 A、4 B、 C、2 D、011. 如图, 是 的外接圆,且 ,在弧AB上取点D(不与点A,B重合),连接 ,则 的度数是( )
A、4 B、 C、2 D、011. 如图, 是 的外接圆,且 ,在弧AB上取点D(不与点A,B重合),连接 ,则 的度数是( )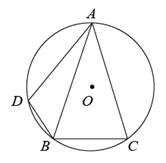 A、60° B、62° C、72° D、73°
A、60° B、62° C、72° D、73°二、填空题
-
12. 北京冬奥会开幕式的巨型雪花状主火炬塔的设计,体现了环保低碳理念.如图所示,它的主体形状呈正六边形.若点A,F,B,D,C,E是正六边形的六个顶点,则tan∠ABE= .
 13. 如图,四边形ABCD是边长为的正方形,曲线DA1B1C1D1A2 …是由多段90°的圆心角所对的弧组成的.其中,弧DA1的圆心为A,半径为AD;弧A1B1的圆心为B,半径为BA1;弧B1C1的圆心为C,半径为CB1;弧C1D1的圆心为D,半径为DC1….弧DA1、弧A1B1、弧B1C1、弧C1D1…的圆心依次按点A,B,C,D循环,则弧C2022D2022的长是(结果保留π).
13. 如图,四边形ABCD是边长为的正方形,曲线DA1B1C1D1A2 …是由多段90°的圆心角所对的弧组成的.其中,弧DA1的圆心为A,半径为AD;弧A1B1的圆心为B,半径为BA1;弧B1C1的圆心为C,半径为CB1;弧C1D1的圆心为D,半径为DC1….弧DA1、弧A1B1、弧B1C1、弧C1D1…的圆心依次按点A,B,C,D循环,则弧C2022D2022的长是(结果保留π).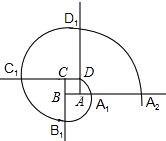 14. 如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,⊙O为Rt△ABC的内切圆,则图中阴影部分的面积为(结果保留π).
14. 如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,⊙O为Rt△ABC的内切圆,则图中阴影部分的面积为(结果保留π).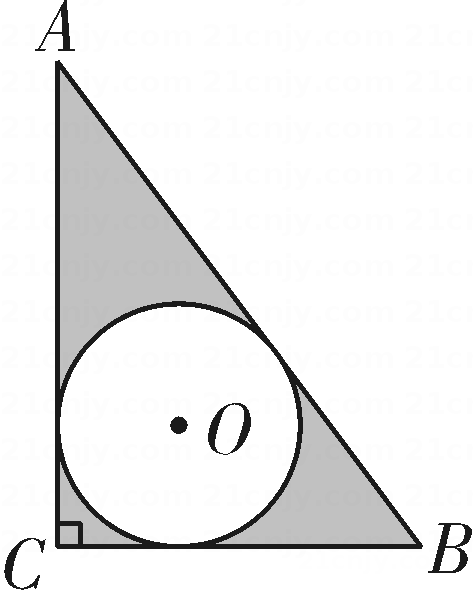 15. 如图,点P是上一点,是一条弦,点C是上一点,与点D关于对称,交于点E,与交于点F,且.给出下面四个结论:①平分; ②; ③; ④为的切线.其中所有正确结论的序号是.
15. 如图,点P是上一点,是一条弦,点C是上一点,与点D关于对称,交于点E,与交于点F,且.给出下面四个结论:①平分; ②; ③; ④为的切线.其中所有正确结论的序号是. 16. 如图,∠DCE是⊙O内接四边形ABCD的一个外角,若∠DCE=72°,那么∠BOD的度数为 .
16. 如图,∠DCE是⊙O内接四边形ABCD的一个外角,若∠DCE=72°,那么∠BOD的度数为 .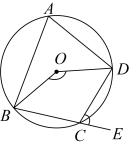 17. 数学小组研究如下问题:遵义市某地的纬度约为北纬28°,求北纬28纬线的长度.
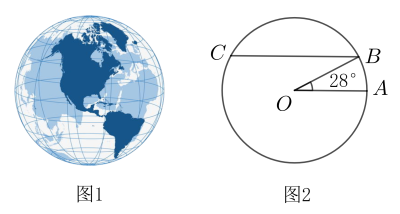
17. 数学小组研究如下问题:遵义市某地的纬度约为北纬28°,求北纬28纬线的长度.小组成员查阅相关资料,得到如下信息:
信息一:如图1,在地球仪上,与赤道平行的圆圈叫做纬线;
信息二:如图2,赤道半径约为6400千米,弦 , 以为直径的圆的周长就是北纬28°纬线的长度;(参考数据: , , , )
根据以上信息,北纬28°纬线的长度约为千米.
 18. 一个扇形的面积为 , 半径为 , 则此扇形的圆心角是度.19. 如图,在平面直角坐标系中,点的坐标为 , 点在轴正半轴上,以点为圆心,长为半径作弧,交轴正半轴于点 , 则点的坐标为 .
18. 一个扇形的面积为 , 半径为 , 则此扇形的圆心角是度.19. 如图,在平面直角坐标系中,点的坐标为 , 点在轴正半轴上,以点为圆心,长为半径作弧,交轴正半轴于点 , 则点的坐标为 .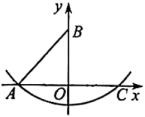 20. 如图,在半径为1的上顺次取点 , , , , , 连接 , , , , , . 若 , , 则与的长度之和为 . (结果保留).
20. 如图,在半径为1的上顺次取点 , , , , , 连接 , , , , , . 若 , , 则与的长度之和为 . (结果保留). 21. 已知为⊙的直径且 , 点是⊙上一点(不与、重合),点在半径上,且 , 与过点的⊙的切线垂直,垂足为 . 若 , 则CD= , OD= .22. 数学课上,老师将如图边长为1的正方形铁丝框变形成以A为圆心, 为半径的扇形(铁丝的粗细忽略不计),则所得扇形 的面积是 .
21. 已知为⊙的直径且 , 点是⊙上一点(不与、重合),点在半径上,且 , 与过点的⊙的切线垂直,垂足为 . 若 , 则CD= , OD= .22. 数学课上,老师将如图边长为1的正方形铁丝框变形成以A为圆心, 为半径的扇形(铁丝的粗细忽略不计),则所得扇形 的面积是 .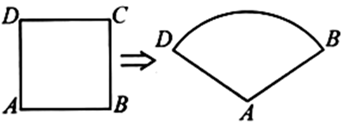 23. 如图,在 网格中,各小正方形边长均为1,点O,A,B,C,D,E均在格点上,点O是 的外心,在不添加其他字母的情况下,则除 外把你认为外心也是O的三角形都写出来 .
23. 如图,在 网格中,各小正方形边长均为1,点O,A,B,C,D,E均在格点上,点O是 的外心,在不添加其他字母的情况下,则除 外把你认为外心也是O的三角形都写出来 . 24. 如图,四边形 是 的内接正四边形,分别以点A,O为圆心,取大于 的定长为半径画弧,两弧相交于点M,N,作直线MN,交 于点E,F.若 ,则 , 所围成的阴影部分面积为.
24. 如图,四边形 是 的内接正四边形,分别以点A,O为圆心,取大于 的定长为半径画弧,两弧相交于点M,N,作直线MN,交 于点E,F.若 ,则 , 所围成的阴影部分面积为.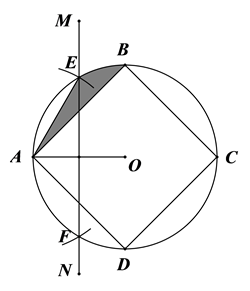
三、综合题
-
25. 如图,AC是⊙O的直径,弦BD交AC于点E,点F为BD延长线上一点,∠DAF=∠B.
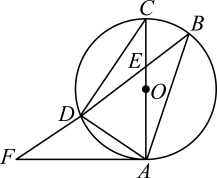 (1)、求证:AF是⊙O的切线;(2)、若⊙O的半径为5,AD是AEF的中线,且AD=6,求AE的长.26. 如图,在中,为的直径,点E在上,D为的中点,连接并延长交于点C.连接 , 在的延长线上取一点F,连接 , 使 .
(1)、求证:AF是⊙O的切线;(2)、若⊙O的半径为5,AD是AEF的中线,且AD=6,求AE的长.26. 如图,在中,为的直径,点E在上,D为的中点,连接并延长交于点C.连接 , 在的延长线上取一点F,连接 , 使 . (1)、求证:为的切线;(2)、若 , 求的半径.27. 如图,△ABC内接于⊙O,AB是⊙O的直径,⊙O的切线PC交BA的延长线于点P,OF∥BC交AC于点E,交PC于点F,连接AF.
(1)、求证:为的切线;(2)、若 , 求的半径.27. 如图,△ABC内接于⊙O,AB是⊙O的直径,⊙O的切线PC交BA的延长线于点P,OF∥BC交AC于点E,交PC于点F,连接AF.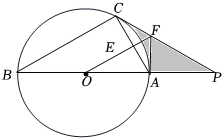 (1)、判断直线AF与⊙O的位置关系并说明理由;(2)、若⊙O的半径为6,AF=2 , 求AC的长;(3)、在(2)的条件下,求阴影部分的面积.28. 如图,AB为⊙O的直径,D、E是⊙O上的两点,延长AB至点C,连接CD,∠BDC=∠BAD.
(1)、判断直线AF与⊙O的位置关系并说明理由;(2)、若⊙O的半径为6,AF=2 , 求AC的长;(3)、在(2)的条件下,求阴影部分的面积.28. 如图,AB为⊙O的直径,D、E是⊙O上的两点,延长AB至点C,连接CD,∠BDC=∠BAD. (1)、求证:CD是⊙O的切线.(2)、若tan∠BED= , AC=9,求⊙O的半径.29. 如图,为的直径,是的切线,为切点,连接.垂直平分 , 垂足为 , 且交于点 , 交于点 , 连接 , .
(1)、求证:CD是⊙O的切线.(2)、若tan∠BED= , AC=9,求⊙O的半径.29. 如图,为的直径,是的切线,为切点,连接.垂直平分 , 垂足为 , 且交于点 , 交于点 , 连接 , .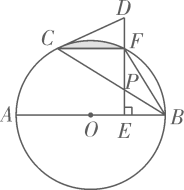 (1)、求证:;(2)、当平分时,求证:;(3)、在(2)的条件下, , 求阴影部分的面积.30. 如图,D是以AB为直径的⊙O上一点,过点D的切线DE交AB的延长线于点E,过点B作BC⊥DE交AD的延长线于点C,垂足为点F.
(1)、求证:;(2)、当平分时,求证:;(3)、在(2)的条件下, , 求阴影部分的面积.30. 如图,D是以AB为直径的⊙O上一点,过点D的切线DE交AB的延长线于点E,过点B作BC⊥DE交AD的延长线于点C,垂足为点F.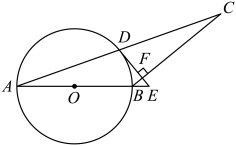 (1)、求证:AB=CB;(2)、若AB=18,sinA= , 求EF的长.31. 如图,正方形内接于 , 点E为的中点,连接交于点F,延长交于点G,连接.
(1)、求证:AB=CB;(2)、若AB=18,sinA= , 求EF的长.31. 如图,正方形内接于 , 点E为的中点,连接交于点F,延长交于点G,连接.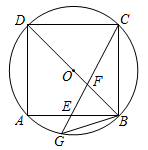 (1)、求证:;(2)、若.求和的长.32. 如图,AB为圆的直径, C是⊙O上一点,过点C的直线交AB的延长线于点M.作AD⊥MC,垂足为D,已知AC平分∠MAD .
(1)、求证:;(2)、若.求和的长.32. 如图,AB为圆的直径, C是⊙O上一点,过点C的直线交AB的延长线于点M.作AD⊥MC,垂足为D,已知AC平分∠MAD . (1)、求证:MC是⊙O的切线:(2)、若 AB=BM=4,求 tan∠MAC的值33. 如图,P为⊙O外一点,PA、PB为⊙O的切线,切点分别为A、B,直线PO交⊙O于点D、E,交AB于点C.
(1)、求证:MC是⊙O的切线:(2)、若 AB=BM=4,求 tan∠MAC的值33. 如图,P为⊙O外一点,PA、PB为⊙O的切线,切点分别为A、B,直线PO交⊙O于点D、E,交AB于点C. (1)、求证:∠ADE=∠PAE.(2)、若∠ADE=30°,求证:AE=PE.(3)、若PE=4,CD=6,求CE的长.34. 综合与实践
(1)、求证:∠ADE=∠PAE.(2)、若∠ADE=30°,求证:AE=PE.(3)、若PE=4,CD=6,求CE的长.34. 综合与实践“善思”小组开展“探究四点共圆的条件”活动,得出结论:对角互补的四边形四个顶点共圆.该小组继续利用上述结论进行探究.
提出问题:
如图1,在线段同侧有两点B,D,连接 , , , , 如果 , 那么A,B,C,D四点在同一个圆上.
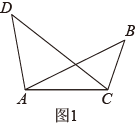
探究展示:
如图2,作经过点A,C,D的 , 在劣弧上取一点E(不与A,C重合),连接 , 则(依据1)

点A,B,C,E四点在同一个圆上(对角互补的四边形四个顶点共圆)
点B,D在点A,C,E所确定的上(依据2)
点A,B,C,E四点在同一个圆上
(1)、反思归纳:上述探究过程中的“依据1”、“依据2”分别是指什么?依据1:;依据2:.
(2)、图3,在四边形中, , , 则的度数为. (3)、展探究:如图4,已知是等腰三角形, , 点D在上(不与的中点重合),连接.作点C关于的对称点E,连接并延长交的延长线于F,连接 , .
(3)、展探究:如图4,已知是等腰三角形, , 点D在上(不与的中点重合),连接.作点C关于的对称点E,连接并延长交的延长线于F,连接 , .
①求证:A,D,B,E四点共圆;
②若 , 的值是否会发生变化,若不变化,求出其值;若变化,请说明理由.
35. 如图,在Rt△ABC中,∠ACB=90°,AO是△ABC的角平分线,以O为圆心,OC为半径作⊙O与直线AO交于点E和点D.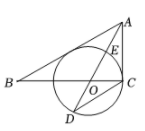 (1)、求证:AB是⊙O的切线;(2)、连接CE,求证:△ACE∽△ADC;(3)、若= , ⊙O的半径为6,求tan∠OAC.36. 如图,AB是⊙O的直径,点C是圆上的一点,CD⊥AD于点D,AD交⊙O于点F,连接AC,若AC平分∠DAB,过点F作FG⊥AB于点G交AC于点H.
(1)、求证:AB是⊙O的切线;(2)、连接CE,求证:△ACE∽△ADC;(3)、若= , ⊙O的半径为6,求tan∠OAC.36. 如图,AB是⊙O的直径,点C是圆上的一点,CD⊥AD于点D,AD交⊙O于点F,连接AC,若AC平分∠DAB,过点F作FG⊥AB于点G交AC于点H. (1)、求证:CD是⊙O的切线;(2)、延长AB和DC交于点E,若AE=4BE,求cos∠DAB的值;(3)、在(2)的条件下,求的值.37. 已知是的直径,点A,点B是上的两个点,连接 , 点D,点E分别是半径的中点,连接 , 且 .
(1)、求证:CD是⊙O的切线;(2)、延长AB和DC交于点E,若AE=4BE,求cos∠DAB的值;(3)、在(2)的条件下,求的值.37. 已知是的直径,点A,点B是上的两个点,连接 , 点D,点E分别是半径的中点,连接 , 且 .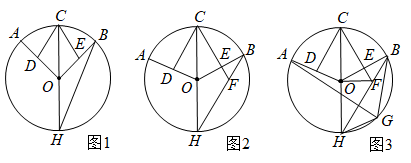 (1)、如图1,求证:;(2)、如图2,延长交于点F,若 , 求证:;(3)、如图3,在(2)的条件下,点G是上一点,连接 , 若 , , 求的长.
(1)、如图1,求证:;(2)、如图2,延长交于点F,若 , 求证:;(3)、如图3,在(2)的条件下,点G是上一点,连接 , 若 , , 求的长.