2022年全国中考数学真题分类汇编20 圆(2)
试卷更新日期:2022-12-29 类型:二轮复习
一、单选题
-
1. 如图,为的直径,弦交于点 , , , , 则( )
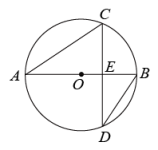 A、 B、 C、1 D、22. 把量角器和含角的三角板按如图方式摆放:零刻度线与长直角边重合,移动量角器使外圆弧与斜边相切时,发现中心恰好在刻度处,短直角边过量角器外沿刻度处(即 , ).则阴影部分的面积为( )
A、 B、 C、1 D、22. 把量角器和含角的三角板按如图方式摆放:零刻度线与长直角边重合,移动量角器使外圆弧与斜边相切时,发现中心恰好在刻度处,短直角边过量角器外沿刻度处(即 , ).则阴影部分的面积为( )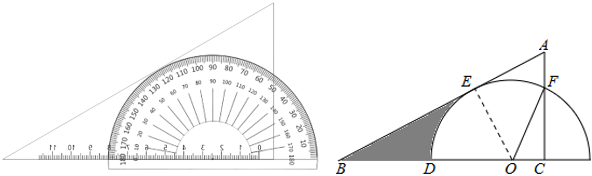 A、 B、 C、 D、3. 我国魏晋时期的数学家刘徽首创割圆术:割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体,而无所失矣",即通过圆内接正多边形割圆,从正六边形开始,每次边数成倍增加,依次可得圆内接正十二边形,内接正二十四边形,…….边数越多割得越细,正多边形的周长就越接近圆的周长.再根据“圆周率等于圆周长与该圆直径的比”来计算圆周率.设圆的半径为R,图1中圆内接正六边形的周长 , 则 . 再利用圆的内接正十二边形来计算圆周率则圆周率约为( )
A、 B、 C、 D、3. 我国魏晋时期的数学家刘徽首创割圆术:割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体,而无所失矣",即通过圆内接正多边形割圆,从正六边形开始,每次边数成倍增加,依次可得圆内接正十二边形,内接正二十四边形,…….边数越多割得越细,正多边形的周长就越接近圆的周长.再根据“圆周率等于圆周长与该圆直径的比”来计算圆周率.设圆的半径为R,图1中圆内接正六边形的周长 , 则 . 再利用圆的内接正十二边形来计算圆周率则圆周率约为( )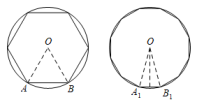 A、 B、 C、 D、4. 如图.将扇形翻折,使点A与圆心O重合,展开后折痕所在直线l与交于点C,连接 . 若 , 则图中阴影部分的面积是( )
A、 B、 C、 D、4. 如图.将扇形翻折,使点A与圆心O重合,展开后折痕所在直线l与交于点C,连接 . 若 , 则图中阴影部分的面积是( )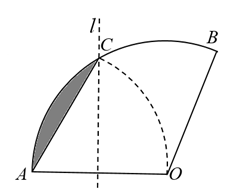 A、 B、 C、 D、5. 如图是“光盘行动”的宣传海报,图中餐盘与筷子可看成直线和圆的位置关系是( )
A、 B、 C、 D、5. 如图是“光盘行动”的宣传海报,图中餐盘与筷子可看成直线和圆的位置关系是( ) A、相切 B、相交 C、相离 D、平行6. 如图,边长为的正方形内接于 , , 分别与相切于点和点 , 的延长线与的延长线交于点 , 则图中阴影部分的面积为( )
A、相切 B、相交 C、相离 D、平行6. 如图,边长为的正方形内接于 , , 分别与相切于点和点 , 的延长线与的延长线交于点 , 则图中阴影部分的面积为( ) A、 B、 C、 D、7. 一个正六边形的内角和的度数为( )A、1080° B、720° C、540° D、360°8. 在2022年北京冬奥会开幕式和闭幕式中,一片“雪花”的故事展现了“世界大同、天下一家”的主题,让世界观众感受了中国人的浪漫,如图,将“雪花”图案(边长为4的正六边形ABCDEF)放在平面直角坐标系中,若AB与x轴垂直,顶点A的坐标为(2,-3).则顶点C的坐标为( )
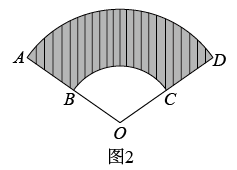
A、 B、 C、 D、7. 一个正六边形的内角和的度数为( )A、1080° B、720° C、540° D、360°8. 在2022年北京冬奥会开幕式和闭幕式中,一片“雪花”的故事展现了“世界大同、天下一家”的主题,让世界观众感受了中国人的浪漫,如图,将“雪花”图案(边长为4的正六边形ABCDEF)放在平面直角坐标系中,若AB与x轴垂直,顶点A的坐标为(2,-3).则顶点C的坐标为( )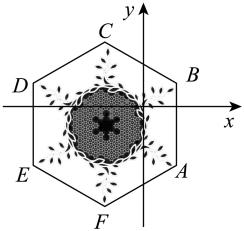 A、 B、 C、 D、9. 已知圆锥的母线长8cm,底面圆的直径6cm,则这个圆锥的侧面积是( )A、96πcm2 B、48πcm2 C、33πcm2 D、24πcm210. 如图1是一块弘扬“社会主义核心价值观”的扇面宣传展板,该展板的部分示意图如图2所示,它是以O为圆心,OA,OB长分别为半径,圆心角 形成的扇面,若 , ,则阴影部分的面积为( )
A、 B、 C、 D、9. 已知圆锥的母线长8cm,底面圆的直径6cm,则这个圆锥的侧面积是( )A、96πcm2 B、48πcm2 C、33πcm2 D、24πcm210. 如图1是一块弘扬“社会主义核心价值观”的扇面宣传展板,该展板的部分示意图如图2所示,它是以O为圆心,OA,OB长分别为半径,圆心角 形成的扇面,若 , ,则阴影部分的面积为( )
 A、 B、 C、 D、11. 如图,圆锥底面圆的半径 ,母线长 ,则这个圆锥的侧面积为( )
A、 B、 C、 D、11. 如图,圆锥底面圆的半径 ,母线长 ,则这个圆锥的侧面积为( ) A、 B、 C、 D、12. 如图,AB是⊙O的直径,C是⊙O上一点,连接AC,OC,若AB=6,∠A=30°,则 的长为( )
A、 B、 C、 D、12. 如图,AB是⊙O的直径,C是⊙O上一点,连接AC,OC,若AB=6,∠A=30°,则 的长为( )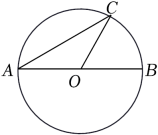 A、6π B、2π C、π D、π
A、6π B、2π C、π D、π二、填空题
-
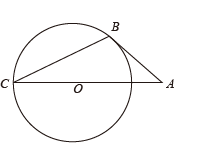
13. 如图,AB切⊙O于点 , AO的延长线交⊙O于点C,连接BC,若∠A=40°,则∠C的度数为 .
 14. 已知⊙O的直径AB长为2,弦AC长为 , 那么弦AC所对的圆周角的度数等于 .15. 如图,在中,半径垂直弦于点 , 若 , , 则 .
14. 已知⊙O的直径AB长为2,弦AC长为 , 那么弦AC所对的圆周角的度数等于 .15. 如图,在中,半径垂直弦于点 , 若 , , 则 . 16. 如图,内接于是直径,过点A作的切线 . 若 , 则的度数是度.
16. 如图,内接于是直径,过点A作的切线 . 若 , 则的度数是度.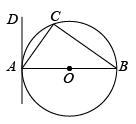 17. 如图,边长为4的正方形ABCD的对角线交于点O,以OC为半径的扇形的圆心角 . 则图中阴影部分面积是 .
17. 如图,边长为4的正方形ABCD的对角线交于点O,以OC为半径的扇形的圆心角 . 则图中阴影部分面积是 .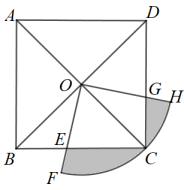 18. 如图,边长为4的正方形ABCD内接于 , 则的长是(结果保留)
18. 如图,边长为4的正方形ABCD内接于 , 则的长是(结果保留) 19. 如图,点A,C,D,B在⊙O上,AC=BC,∠ACB=90°.若CD=a,tan∠CBD= , 则AD的长是 .
19. 如图,点A,C,D,B在⊙O上,AC=BC,∠ACB=90°.若CD=a,tan∠CBD= , 则AD的长是 .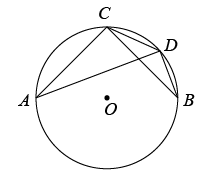 20. 如图,等边三角形ABC内接于⊙O,BC=2 , 则图中阴影部分的面积是 .
20. 如图,等边三角形ABC内接于⊙O,BC=2 , 则图中阴影部分的面积是 .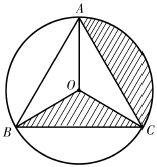
三、作图题
-
21. 综合与实践
问题情境:我国东周到汉代一些出土实物上反映出一些几何作图方法,如侯马铸铜遗址出土车軎范、芯组成的(如图1),它的端面是圆形,如图2是用“矩”(带直角的角尺)确定端面圆心的方法:将“矩”的直角尖端A沿圆周移动,直到 ,在圆上标记A,B,C三点;将“矩”向右旋转,使它左侧边落在A,B点上,“矩”的另一条边与圆的交点标记为D点,这样就用“矩”确定了圆上等距离的A,B,C,D四点,连接AD,BC相交于点O,即O为圆心.
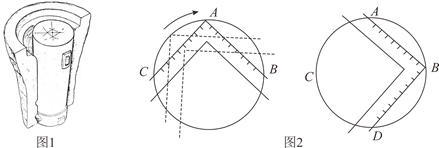
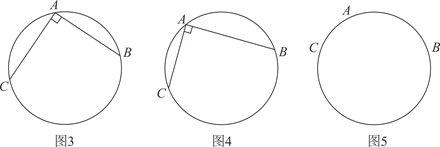 (1)、问题解决:请你根据“问题情境”中提供的方法,用三角板还原我国古代几何作图确定圆心O.如图3,点A,B,C在 上, ,且 ,请作出圆心O.(保留作图痕迹,不写作法)(2)、类比迁移:小梅受此问题的启发,在研究了用“矩”(带直角的角尺)确定端面圆心的方法后发现,如果AB和AC不相等,用三角板也可以确定圆心O.如图4,点A,B,C在 上, ,请作出圆心O.(保留作图痕迹,不写作法)(3)、拓展探究:小梅进一步研究,发现古代由“矩”度量确定圆上等距离点时存在误差,用平时学的尺规作图的方法确定圆心可以减少误差.如图5,点A,B,C是 上任意三点,请用不带刻度的直尺和圆规作出圆心O.(保留作图痕迹,不写作法)请写出你确定圆心的理由: ▲ .
(1)、问题解决:请你根据“问题情境”中提供的方法,用三角板还原我国古代几何作图确定圆心O.如图3,点A,B,C在 上, ,且 ,请作出圆心O.(保留作图痕迹,不写作法)(2)、类比迁移:小梅受此问题的启发,在研究了用“矩”(带直角的角尺)确定端面圆心的方法后发现,如果AB和AC不相等,用三角板也可以确定圆心O.如图4,点A,B,C在 上, ,请作出圆心O.(保留作图痕迹,不写作法)(3)、拓展探究:小梅进一步研究,发现古代由“矩”度量确定圆上等距离点时存在误差,用平时学的尺规作图的方法确定圆心可以减少误差.如图5,点A,B,C是 上任意三点,请用不带刻度的直尺和圆规作出圆心O.(保留作图痕迹,不写作法)请写出你确定圆心的理由: ▲ .四、综合题
-
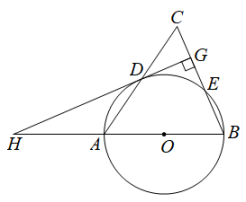
22. 如图,的直径垂直于弦于点F,点P在的延长线上,与相切于点C.
 (1)、求证:;(2)、若的直径为4,弦平分半径 , 求:图中阴影部分的面积.23. 如图,C,D是以AB为直径的半圆上的两点, , 连结BC,CD.
(1)、求证:;(2)、若的直径为4,弦平分半径 , 求:图中阴影部分的面积.23. 如图,C,D是以AB为直径的半圆上的两点, , 连结BC,CD. (1)、求证: .(2)、若 , , 求阴影部分的面积.24. 四边形内接于 , 直径与弦交于点 , 直线与相切于点 .
(1)、求证: .(2)、若 , , 求阴影部分的面积.24. 四边形内接于 , 直径与弦交于点 , 直线与相切于点 .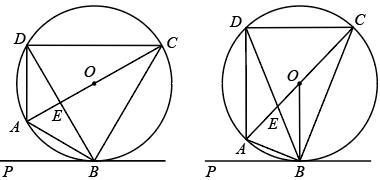 (1)、如图1,若 , 且 , 求证:平分;(2)、如图2,连接 , 若 , 求证: .25. 如图,已知BC为⊙O的直径,点D为的中点,过点D作DG∥CE,交BC的延长线于点A,连接BD,交CE于点F.
(1)、如图1,若 , 且 , 求证:平分;(2)、如图2,连接 , 若 , 求证: .25. 如图,已知BC为⊙O的直径,点D为的中点,过点D作DG∥CE,交BC的延长线于点A,连接BD,交CE于点F.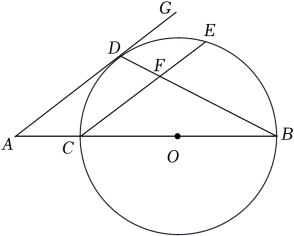 (1)、求证:AD是⊙O的切线;(2)、若EF=3,CF=5,tan∠GDB=2,求AC的长.26. 如图,AB是半圆O的直径,点C在半圆O上,点D为的中点,连接AC,BC,AD,AD与BC相交于点G,过点D作直线DEBC,交AC的延长线于点E.
(1)、求证:AD是⊙O的切线;(2)、若EF=3,CF=5,tan∠GDB=2,求AC的长.26. 如图,AB是半圆O的直径,点C在半圆O上,点D为的中点,连接AC,BC,AD,AD与BC相交于点G,过点D作直线DEBC,交AC的延长线于点E.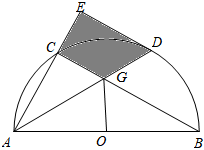 (1)、求证:DE是⊙O的切线;(2)、若 , CG=2 , 求阴影部分的面积.27. 如图,以线段为直径作 , 交射线于点 , 平分交于点 , 过点作直线于点 , 交的延长线于点 . 连接并延长交于点 .
(1)、求证:DE是⊙O的切线;(2)、若 , CG=2 , 求阴影部分的面积.27. 如图,以线段为直径作 , 交射线于点 , 平分交于点 , 过点作直线于点 , 交的延长线于点 . 连接并延长交于点 .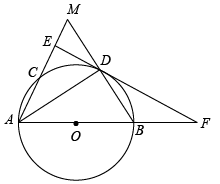 (1)、求证:直线是的切线;(2)、求证:;(3)、若 , , 求的长.28. 如图是直径,A是上异于C,D的一点,点B是延长线上一点,连接、、 , 且 .
(1)、求证:直线是的切线;(2)、求证:;(3)、若 , , 求的长.28. 如图是直径,A是上异于C,D的一点,点B是延长线上一点,连接、、 , 且 .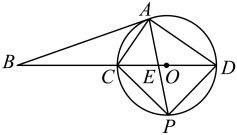 (1)、求证:直线是的切线;(2)、若 , 求的值;(3)、在(2)的条件下,作的平分线交于P,交于E,连接、 , 若 , 求的值.29. 牂狗江“佘月郎山,西陵晚渡”的风景描绘中有半个月亮挂在山上,月亮之上有个“齐天大圣”守护洞口的传说.真实情况是老王山上有个月亮洞,洞顶上经常有猴子爬来爬去,下图是月亮洞的截面示意图.
(1)、求证:直线是的切线;(2)、若 , 求的值;(3)、在(2)的条件下,作的平分线交于P,交于E,连接、 , 若 , 求的值.29. 牂狗江“佘月郎山,西陵晚渡”的风景描绘中有半个月亮挂在山上,月亮之上有个“齐天大圣”守护洞口的传说.真实情况是老王山上有个月亮洞,洞顶上经常有猴子爬来爬去,下图是月亮洞的截面示意图.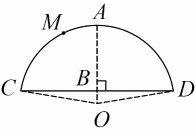 (1)、科考队测量出月亮洞的洞宽约是28m,洞高约是12m,通过计算截面所在圆的半径可以解释月亮洞像半个月亮,求半径的长(结果精确到0.1m);(2)、若 , 点在上,求的度数,并用数学知识解释为什么“齐天大圣”点在洞顶上巡视时总能看清洞口的情况.30. 如图,是的直径,点是劣弧上一点, , 且 , 平分 , 与交于点 .
(1)、科考队测量出月亮洞的洞宽约是28m,洞高约是12m,通过计算截面所在圆的半径可以解释月亮洞像半个月亮,求半径的长(结果精确到0.1m);(2)、若 , 点在上,求的度数,并用数学知识解释为什么“齐天大圣”点在洞顶上巡视时总能看清洞口的情况.30. 如图,是的直径,点是劣弧上一点, , 且 , 平分 , 与交于点 . (1)、求证:是的切线;(2)、若 , 求的长;(3)、延长 , 交于点 , 若 , 求的半径.31. 如图,在中, , 以AB为直径作⊙ , 分别交BC于点D,交AC于点E, , 垂足为H,连接DE并延长交BA的延长线于点F.
(1)、求证:是的切线;(2)、若 , 求的长;(3)、延长 , 交于点 , 若 , 求的半径.31. 如图,在中, , 以AB为直径作⊙ , 分别交BC于点D,交AC于点E, , 垂足为H,连接DE并延长交BA的延长线于点F. (1)、求证:DH是⊙的切线;(2)、若E为AH的中点,求的值.32. 如图,AB为⊙O的直径,C为圆上的一点,D为劣弧的中点,过点D作⊙O的切线与AC的延长线交于点P,与AB的延长线交于点F,AD与BC交于点E.
(1)、求证:DH是⊙的切线;(2)、若E为AH的中点,求的值.32. 如图,AB为⊙O的直径,C为圆上的一点,D为劣弧的中点,过点D作⊙O的切线与AC的延长线交于点P,与AB的延长线交于点F,AD与BC交于点E.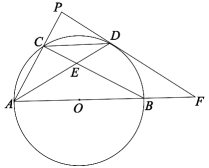 (1)、求证:;(2)、若⊙O的半径为 , DE=1,求AE的长度;(3)、在(2)的条件下,求的面积.33. 如图,在Rt△ABC中,∠B=90°,AE平分∠BAC交BC于点E,O为AC上一点,经过点A、E的⊙O分别交AB、AC于点D、F,连接OD交AE于点M.
(1)、求证:;(2)、若⊙O的半径为 , DE=1,求AE的长度;(3)、在(2)的条件下,求的面积.33. 如图,在Rt△ABC中,∠B=90°,AE平分∠BAC交BC于点E,O为AC上一点,经过点A、E的⊙O分别交AB、AC于点D、F,连接OD交AE于点M. (1)、求证:BC是⊙O的切线.(2)、若CF=2,sinC= , 求AE的长.34. 如图,C是圆O被直径AB分成的半圆上一点,过点C的圆O的切线交AB的延长线于点P,连接CA,CO,CB.
(1)、求证:BC是⊙O的切线.(2)、若CF=2,sinC= , 求AE的长.34. 如图,C是圆O被直径AB分成的半圆上一点,过点C的圆O的切线交AB的延长线于点P,连接CA,CO,CB.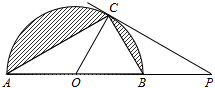 (1)、求证:∠ACO=∠BCP;(2)、若∠ABC=2∠BCP,求∠P的度数;(3)、在(2)的条件下,若AB=4,求图中阴影部分的面积(结果保留π和根号).35. 如图,四边形内接于圆 , 是圆的直径, , 的延长线交于点 , 延长交于点 , .
(1)、求证:∠ACO=∠BCP;(2)、若∠ABC=2∠BCP,求∠P的度数;(3)、在(2)的条件下,若AB=4,求图中阴影部分的面积(结果保留π和根号).35. 如图,四边形内接于圆 , 是圆的直径, , 的延长线交于点 , 延长交于点 , .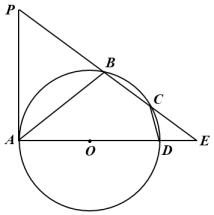 (1)、求证:是圆的切线;(2)、连接 , , , 的长为 .36. 如图,在Rt△ABC中,∠C=90°,∠B=30°,点D为边AB的中点,点O在边BC上,以点O为圆心的圆过顶点C,与边AB交于点D.
(1)、求证:是圆的切线;(2)、连接 , , , 的长为 .36. 如图,在Rt△ABC中,∠C=90°,∠B=30°,点D为边AB的中点,点O在边BC上,以点O为圆心的圆过顶点C,与边AB交于点D. (1)、求证:直线AB是⊙O的切线;(2)、若 , 求图中阴影部分的面积.37. 如图, 是 的外接圆,AB是直径, ,连接AD, ,AC与OD相交于点E.
(1)、求证:直线AB是⊙O的切线;(2)、若 , 求图中阴影部分的面积.37. 如图, 是 的外接圆,AB是直径, ,连接AD, ,AC与OD相交于点E. (1)、求证:AD是 的切线;(2)、若 , ,求 的半径.38. 如图,已知 是 的直径,点 是 上异于 , 的点,点 是 的中点,连接 , , ,过点 作 交 的延长线于点 ,交 的延长线于点 , 的平分线 交 于点 ,交 于点 .
(1)、求证:AD是 的切线;(2)、若 , ,求 的半径.38. 如图,已知 是 的直径,点 是 上异于 , 的点,点 是 的中点,连接 , , ,过点 作 交 的延长线于点 ,交 的延长线于点 , 的平分线 交 于点 ,交 于点 . (1)、求证: 是 的切线;(2)、求 的值;(3)、若 , ,求 的直径.
(1)、求证: 是 的切线;(2)、求 的值;(3)、若 , ,求 的直径.
-