2022年全国中考数学真题分类汇编20 圆(1)
试卷更新日期:2022-12-29 类型:二轮复习
一、单选题
-
1. 如图,四边形是的内接四边形,若 , 则的度数是( )
 A、 B、 C、 D、2. 将一枚飞镖任意投掷到如图所示的正六边形镖盘上,若飞镖落在镖盘上各点的机会相等,则飞镖落在阴影区域的概率为( )
A、 B、 C、 D、2. 将一枚飞镖任意投掷到如图所示的正六边形镖盘上,若飞镖落在镖盘上各点的机会相等,则飞镖落在阴影区域的概率为( ) A、 B、 C、 D、3. 如图,AB是圆O的直径,弦AD平分∠BAC,过点D的切线交AC于点E,∠EAD=25°,则下列结论错误的是( )
A、 B、 C、 D、3. 如图,AB是圆O的直径,弦AD平分∠BAC,过点D的切线交AC于点E,∠EAD=25°,则下列结论错误的是( ) A、AE⊥DE B、AE//OD C、DE=OD D、∠BOD=50°4. 如图,在 的长方形网格飞镖游戏板中,每块小正方形除颜色外都相同,小正方形的顶点称为格点,扇形OAB的圆心及弧的两端均为格点.假设飞镖击中每一块小正方形是等可能的(击中扇形的边界或没有击中游戏板,则重投1次),任意投掷飞镖1次,飞镖击中扇形OAB(阴影部分)的概率是( )
A、AE⊥DE B、AE//OD C、DE=OD D、∠BOD=50°4. 如图,在 的长方形网格飞镖游戏板中,每块小正方形除颜色外都相同,小正方形的顶点称为格点,扇形OAB的圆心及弧的两端均为格点.假设飞镖击中每一块小正方形是等可能的(击中扇形的边界或没有击中游戏板,则重投1次),任意投掷飞镖1次,飞镖击中扇形OAB(阴影部分)的概率是( )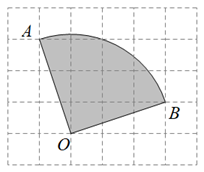 A、 B、 C、 D、5. 如图,有一个半径为2的圆形时钟,其中每个刻度间的弧长均相等,过9点和11点的位置作一条线段,则钟面中阴影部分的面积为( )
A、 B、 C、 D、5. 如图,有一个半径为2的圆形时钟,其中每个刻度间的弧长均相等,过9点和11点的位置作一条线段,则钟面中阴影部分的面积为( )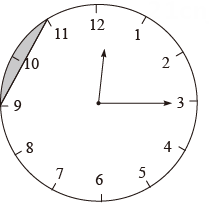 A、 B、 C、 D、6. 某款“不倒翁”(图1)的主视图是图2,PA , PB分别与 所在圆相切于点A , B . 若该圆半径是9cm,∠P=40°,则 的长是( )
A、 B、 C、 D、6. 某款“不倒翁”(图1)的主视图是图2,PA , PB分别与 所在圆相切于点A , B . 若该圆半径是9cm,∠P=40°,则 的长是( )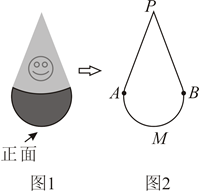 A、 cm B、 cm C、 cm D、 cm7. 如图,内接于 , AD是的直径,若 , 则的度数是( )
A、 cm B、 cm C、 cm D、 cm7. 如图,内接于 , AD是的直径,若 , 则的度数是( ) A、60° B、65° C、70° D、75°8. 如图,扇形纸片AOB的半径为3,沿AB折叠扇形纸片,点O恰好落在上的点C处,图中阴影部分的面积为( )
A、60° B、65° C、70° D、75°8. 如图,扇形纸片AOB的半径为3,沿AB折叠扇形纸片,点O恰好落在上的点C处,图中阴影部分的面积为( )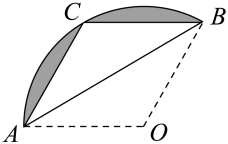 A、 B、 C、 D、9. 实验学校的花坛形状如图所示,其中,等圆⊙O1与⊙O2的半径为3米,且⊙O1经过⊙O2的圆心O2 . 已知实线部分为此花坛的周长,则花坛的周长为( )
A、 B、 C、 D、9. 实验学校的花坛形状如图所示,其中,等圆⊙O1与⊙O2的半径为3米,且⊙O1经过⊙O2的圆心O2 . 已知实线部分为此花坛的周长,则花坛的周长为( ) A、4π米 B、6π米 C、8π米 D、12π米10. 正多边形的每个内角为 , 则它的边数是( )A、4 B、6 C、7 D、511. 如图,由边长为1的小正方形构成的网格中,点 , , 都在格点上,以为直径的圆经过点 , , 则的值为( )
A、4π米 B、6π米 C、8π米 D、12π米10. 正多边形的每个内角为 , 则它的边数是( )A、4 B、6 C、7 D、511. 如图,由边长为1的小正方形构成的网格中,点 , , 都在格点上,以为直径的圆经过点 , , 则的值为( ) A、 B、 C、 D、12. 如图,是的直径,将弦绕点顺时针旋转得到 , 此时点的对应点落在上,延长 , 交于点 , 若 , 则图中阴影部分的面积为( )
A、 B、 C、 D、12. 如图,是的直径,将弦绕点顺时针旋转得到 , 此时点的对应点落在上,延长 , 交于点 , 若 , 则图中阴影部分的面积为( )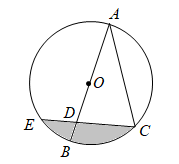 A、 B、 C、 D、13. 如图所示,圆锥形烟囱帽的底面半径为 , 侧面展开图为半圆形,则它的母线长为( )
A、 B、 C、 D、13. 如图所示,圆锥形烟囱帽的底面半径为 , 侧面展开图为半圆形,则它的母线长为( )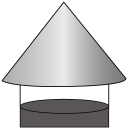 A、 B、 C、 D、14. 如图,是的两条直径,E是劣弧的中点,连接 , . 若 , 则的度数为( )
A、 B、 C、 D、14. 如图,是的两条直径,E是劣弧的中点,连接 , . 若 , 则的度数为( )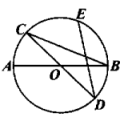 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
15. 若圆锥的底面圆半径为2,母线长为5,则该圆锥的侧面积是.(结果保留)16. 如图,A、B、C点在圆O上, 若∠ACB=36°, 则∠AOB= .
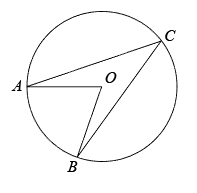 17. △ABC是边长为5的等边三角形,△DCE是边长为3的等边三角形,直线BD与直线AE交于点F.如图,若点D在△ABC内,∠DBC=20°,则∠BAF=°;现将△DCE绕点C旋转1周,在这个旋转过程中,线段AF长度的最小值是.
17. △ABC是边长为5的等边三角形,△DCE是边长为3的等边三角形,直线BD与直线AE交于点F.如图,若点D在△ABC内,∠DBC=20°,则∠BAF=°;现将△DCE绕点C旋转1周,在这个旋转过程中,线段AF长度的最小值是.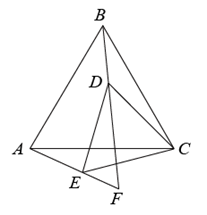 18. 如图,AB是 的直径,弦CD交AB于点E,连接AC,AD.若 ,则 °
18. 如图,AB是 的直径,弦CD交AB于点E,连接AC,AD.若 ,则 °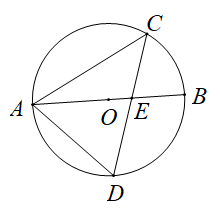 19. 如图, 是 的直径, 是 的切线, 为切点,连接 ,与 交于点 ,连接 .若 ,则 .
19. 如图, 是 的直径, 是 的切线, 为切点,连接 ,与 交于点 ,连接 .若 ,则 . 20. 如图, 是 的直径,点 在 上,若 ,则 °.
20. 如图, 是 的直径,点 在 上,若 ,则 °. 21. 如图,沿一条母线将圆锥侧面剪开并展平,得到一个扇形,若母线长 为 ,扇形的圆心角 ,则圆锥的底面圆半径 为 .
21. 如图,沿一条母线将圆锥侧面剪开并展平,得到一个扇形,若母线长 为 ,扇形的圆心角 ,则圆锥的底面圆半径 为 . 22. 如图,是的外接圆,为直径,若 , , 点从点出发,在内运动且始终保持 , 当 , 两点距离最小时,动点的运动路径长为 .
22. 如图,是的外接圆,为直径,若 , , 点从点出发,在内运动且始终保持 , 当 , 两点距离最小时,动点的运动路径长为 . 23. 如图,从一个边长是的正五边形纸片上剪出一个扇形,这个扇形的面积为(用含的代数式表示);如果将剪下来的扇形围成一个圆锥,圆锥的底面圆直径为 .
23. 如图,从一个边长是的正五边形纸片上剪出一个扇形,这个扇形的面积为(用含的代数式表示);如果将剪下来的扇形围成一个圆锥,圆锥的底面圆直径为 . 24. 如图,已知的半径为2,是的弦.若 , 则劣弧的长为 .
24. 如图,已知的半径为2,是的弦.若 , 则劣弧的长为 .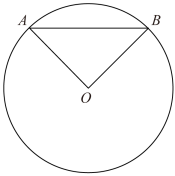
三、作图题
-
25. 如图,在每个小正方形的边长为1的网格中,圆上的点A,B,C及的一边上的点E,F均在格点上.
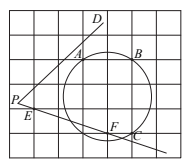 (1)、线段的长等于;(2)、若点M,N分别在射线上,满足且 . 请用无刻度的直尺,在如图所示的网格中,画出点M,N,并简要说明点M,N的位置是如何找到的(不要求证明) .
(1)、线段的长等于;(2)、若点M,N分别在射线上,满足且 . 请用无刻度的直尺,在如图所示的网格中,画出点M,N,并简要说明点M,N的位置是如何找到的(不要求证明) .四、解答题
-
26. 如图1是一张圆凳的造型,已知这张圆凳的上、下底面圆的直径都是 , 高为 . 它被平行于上、下底面的平面所截得的横截面都是圆.小明画出了它的主视图,是由上、下底面圆的直径、以及、组成的轴对称图形,直线为对称轴,点、分别是、的中点,如图2,他又画出了所在的扇形并度量出扇形的圆心角 , 发现并证明了点在上.请你继续完成长的计算.
参考数据: , , , , , .

五、综合题
-
27. 如图,是的内接三角形, , 经过圆心交于点 , 连接 , .
 (1)、判断直线与的位置关系,并说明理由;(2)、若 , 求图中阴影部分的面积.28. 已知:△ABC中,D 为BC边上的一点.
(1)、判断直线与的位置关系,并说明理由;(2)、若 , 求图中阴影部分的面积.28. 已知:△ABC中,D 为BC边上的一点. (1)、如图①,过点D作DE∥AB交AC边于点E,若AB=5,BD=9,DC=6,求DE的长;(2)、在图②,用无刻度的直尺和圆规在AC边上做点F,使∠DFA=∠A;(保留作图痕迹,不要求写作法)(3)、如图③,点F在AC边上,连接BF、DF,若∠DFA=∠A,△FBC的面积等于 , 以FD为半径作⊙F,试判断直线BC与⊙F的位置关系,并说明理由.29. 如图,边长为6的等边三角形ABC内接于⊙O,点D为AC上的动点(点A、C除外),BD的延长线交⊙O于点E,连接CE.
(1)、如图①,过点D作DE∥AB交AC边于点E,若AB=5,BD=9,DC=6,求DE的长;(2)、在图②,用无刻度的直尺和圆规在AC边上做点F,使∠DFA=∠A;(保留作图痕迹,不要求写作法)(3)、如图③,点F在AC边上,连接BF、DF,若∠DFA=∠A,△FBC的面积等于 , 以FD为半径作⊙F,试判断直线BC与⊙F的位置关系,并说明理由.29. 如图,边长为6的等边三角形ABC内接于⊙O,点D为AC上的动点(点A、C除外),BD的延长线交⊙O于点E,连接CE.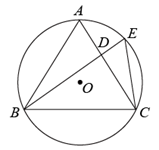 (1)、求证 ;(2)、当 时,求CE的长.30. 如图,在△ABC中,∠ABC =45°,AB=AC,以AB为直径的⊙O与边BC交于点D.
(1)、求证 ;(2)、当 时,求CE的长.30. 如图,在△ABC中,∠ABC =45°,AB=AC,以AB为直径的⊙O与边BC交于点D. (1)、判断直线与⊙的位置关系,并说明理由;(2)、若 , 求图中阴影部分的面积.31. 如图,在网格中,每个小正方形的边长均为1,每个小正方形的顶点称为格点,点、、、、均为格点.
(1)、判断直线与⊙的位置关系,并说明理由;(2)、若 , 求图中阴影部分的面积.31. 如图,在网格中,每个小正方形的边长均为1,每个小正方形的顶点称为格点,点、、、、均为格点.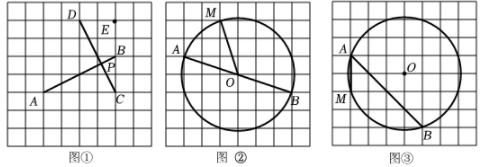 (1)、【操作探究】在数学活动课上,佳佳同学在如图①的网格中,用无刻度的直尺画了两条互相垂直的线段、 , 相交于点并给出部分说理过程,请你补充完整:
(1)、【操作探究】在数学活动课上,佳佳同学在如图①的网格中,用无刻度的直尺画了两条互相垂直的线段、 , 相交于点并给出部分说理过程,请你补充完整:解:在网格中取格点 , 构建两个直角三角形,分别是△ABC和△CDE.
在Rt△ABC中,
在Rt△CDE中, ,
所以.
所以∠=∠.
因为∠∠ =∠ =90°,
所以∠ +∠ =90°,
所以∠ =90°,
即⊥.
(2)、【拓展应用】如图②是以格点为圆心,为直径的圆,请你只用无刻度的直尺,在上找出一点P,使 , 写出作法,并给出证明:(3)、【拓展应用】如图③是以格点为圆心的圆,请你只用无刻度的直尺,在弦上找出一点P.使=· , 写出作法,不用证明.32. 如图,为的弦,交于点 , 交过点的直线于点 , 且.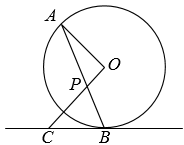 (1)、试判断直线与的位置关系,并说明理由;(2)、若 , 求的长.33. 如图,在⊙O中,AB为直径,P为AB上一点,PA=1,PB=m(m为常数,且m>0).过点P的弦CD⊥AB,Q为 上一动点(与点B不重合),AH⊥QD,垂足为H.连接AD、BQ.
(1)、试判断直线与的位置关系,并说明理由;(2)、若 , 求的长.33. 如图,在⊙O中,AB为直径,P为AB上一点,PA=1,PB=m(m为常数,且m>0).过点P的弦CD⊥AB,Q为 上一动点(与点B不重合),AH⊥QD,垂足为H.连接AD、BQ.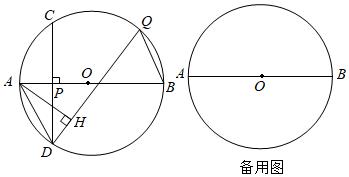 (1)、若m=3.
(1)、若m=3.①求证:∠OAD=60°;
②求 的值;
(2)、用含m的代数式表示 ,请直接写出结果;(3)、存在一个大小确定的⊙O,对于点Q的任意位置,都有BQ2﹣2DH2+PB2的值是一个定值,求此时∠Q的度数.34. 如图,是的直径,是的一条弦,连接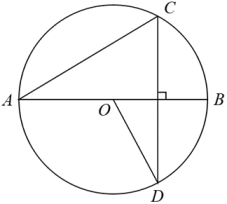 (1)、求证:(2)、连接 , 过点作交的延长线于点 , 延长交于点 , 若为的中点,求证:直线为的切线.35. 在平面直角坐标系中,已知点对于点给出如下定义:将点向右或向左平移个单位长度,再向上或向下平移个单位长度,得到点 , 点关于点的对称点为 , 称点为点的“对应点”.(1)、如图,点点在线段的延长线上,若点点为点的“对应点”.
(1)、求证:(2)、连接 , 过点作交的延长线于点 , 延长交于点 , 若为的中点,求证:直线为的切线.35. 在平面直角坐标系中,已知点对于点给出如下定义:将点向右或向左平移个单位长度,再向上或向下平移个单位长度,得到点 , 点关于点的对称点为 , 称点为点的“对应点”.(1)、如图,点点在线段的延长线上,若点点为点的“对应点”.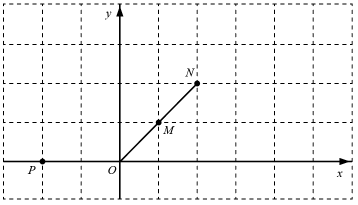
①在图中画出点;
②连接交线段于点求证:
(2)、的半径为1,是上一点,点在线段上,且 , 若为外一点,点为点的“对应点”,连接当点在上运动时直接写出长的最大值与最小值的差(用含的式子表示)36. 已知为的直径, , C为上一点,连接 . (1)、如图①,若C为的中点,求的大小和的长;(2)、如图②,若为的半径,且 , 垂足为E,过点D作的切线,与的延长线相交于点F,求的长.37. 如图,以AB为直径的⊙O与△ABC的边BC相切于点B,且与AC边交于点D,点E为BC中点,连接DE、BD.
(1)、如图①,若C为的中点,求的大小和的长;(2)、如图②,若为的半径,且 , 垂足为E,过点D作的切线,与的延长线相交于点F,求的长.37. 如图,以AB为直径的⊙O与△ABC的边BC相切于点B,且与AC边交于点D,点E为BC中点,连接DE、BD.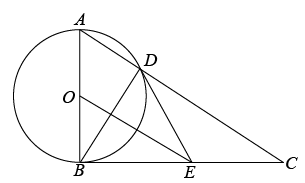 (1)、求证:DE是⊙O的切线;(2)、若DE=5,cos∠ABD= , 求OE的长.38. 如图,在中, , 以为圆心,的长为半径的圆交边于点 , 点在边上且 , 延长交的延长线于点 .
(1)、求证:DE是⊙O的切线;(2)、若DE=5,cos∠ABD= , 求OE的长.38. 如图,在中, , 以为圆心,的长为半径的圆交边于点 , 点在边上且 , 延长交的延长线于点 . (1)、求证:是圆的切线;(2)、已知 , , 求长度及阴影部分面积.
(1)、求证:是圆的切线;(2)、已知 , , 求长度及阴影部分面积.
-
-