2022年全国中考数学真题分类汇编19 四边形及多边形(4)
试卷更新日期:2022-12-29 类型:二轮复习
一、单选题
-
1. 如图,在四边形ABCD中,∠A=∠B=90°,AD=10cm,BC=8cm,点P从点D出发,以1cm/s的速度向点A运动,点M从点B同时出发,以相同的速度向点C运动,当其中一个动点到达端点时,两个动点同时停止运动.设点P的运动时间为t(单位:s),下列结论正确的是( )
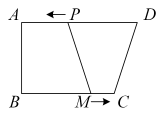 A、当时,四边形ABMP为矩形 B、当时,四边形CDPM为平行四边形 C、当时, D、当时,或6s2. 如图,剪两张对边平行的纸条,随意交叉叠放在一起,重合部分构成一个四边形 , 其中一张纸条在转动过程中,下列结论一定成立的是( )
A、当时,四边形ABMP为矩形 B、当时,四边形CDPM为平行四边形 C、当时, D、当时,或6s2. 如图,剪两张对边平行的纸条,随意交叉叠放在一起,重合部分构成一个四边形 , 其中一张纸条在转动过程中,下列结论一定成立的是( )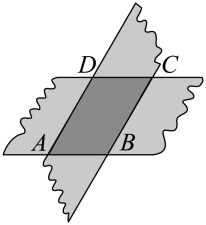 A、四边形周长不变 B、 C、四边形面积不变 D、3. 如图,菱形 , 点、、、均在坐标轴上, , 点 , 点是的中点,点是上的一动点,则的最小值是( )
A、四边形周长不变 B、 C、四边形面积不变 D、3. 如图,菱形 , 点、、、均在坐标轴上, , 点 , 点是的中点,点是上的一动点,则的最小值是( )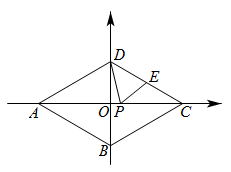 A、3 B、5 C、 D、4. 如图,在矩形中, , 点E,F分别在边上, , AF与相交于点O,连接 , 若 , 则与之间的数量关系正确的是( )
A、3 B、5 C、 D、4. 如图,在矩形中, , 点E,F分别在边上, , AF与相交于点O,连接 , 若 , 则与之间的数量关系正确的是( )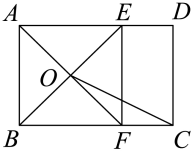 A、 B、 C、 D、5. 如图,四边形是菱形, , 点是中点,是对角线上一点,且 , 则的值是( )
A、 B、 C、 D、5. 如图,四边形是菱形, , 点是中点,是对角线上一点,且 , 则的值是( )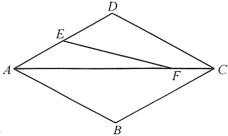 A、3 B、 C、 D、6. 下列命题中,是真命题的有( )
A、3 B、 C、 D、6. 下列命题中,是真命题的有( )①对角线相等且互相平分的四边形是矩形②对角线互相垂直的四边形是菱形③四边相等的四边形是正方形④四边相等的四边形是菱形
A、①② B、①④ C、②③ D、③④7. 如图,在 ABCD中, , ,点E在AD上, ,则 的值是( )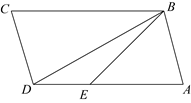 A、 B、 C、 D、8. 若顺次连接四边形 各边的中点所得的四边形是正方形,则四边形 的两条对角线 一定是( )A、互相平分 B、互相垂直 C、互相平分且相等 D、互相垂直且相等9. 如图,在边长为2的等边三角形的外侧作正方形 , 过点作 , 垂足为 , 则的长为( )
A、 B、 C、 D、8. 若顺次连接四边形 各边的中点所得的四边形是正方形,则四边形 的两条对角线 一定是( )A、互相平分 B、互相垂直 C、互相平分且相等 D、互相垂直且相等9. 如图,在边长为2的等边三角形的外侧作正方形 , 过点作 , 垂足为 , 则的长为( ) A、 B、 C、 D、10. 如图,现有一把直尺和一块三角尺,其中 , , AB=8,点A对应直尺的刻度为12.将该三角尺沿着直尺边缘平移,使得△ABC移动到 , 点对应直尺的刻度为0,则四边形的面积是( )
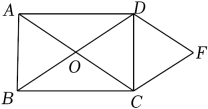
A、 B、 C、 D、10. 如图,现有一把直尺和一块三角尺,其中 , , AB=8,点A对应直尺的刻度为12.将该三角尺沿着直尺边缘平移,使得△ABC移动到 , 点对应直尺的刻度为0,则四边形的面积是( )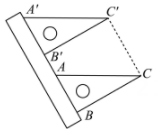 A、96 B、 C、192 D、11. 如图,点 , 将线段平移得到线段 , 若 , 则点D的坐标是( )
A、96 B、 C、192 D、11. 如图,点 , 将线段平移得到线段 , 若 , 则点D的坐标是( )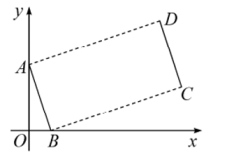 A、 B、 C、 D、12. 如图,菱形中,点E是边的中点,垂直交的延长线于点F,若 , 则菱形的边长是( )
A、 B、 C、 D、12. 如图,菱形中,点E是边的中点,垂直交的延长线于点F,若 , 则菱形的边长是( )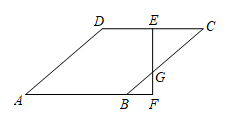 A、3 B、4 C、5 D、13. 矩形纸片中,E为的中点,连接 , 将沿折叠得到 , 连接.若 , , 则的长是( )
A、3 B、4 C、5 D、13. 矩形纸片中,E为的中点,连接 , 将沿折叠得到 , 连接.若 , , 则的长是( )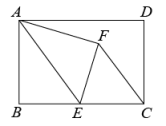 A、3 B、 C、 D、
A、3 B、 C、 D、二、填空题
-
14. 如图,菱形的对角线相交于点O,点E在上,连接 , 点F为的中点,连接 , 若 , , , 则线段的长为 .
 15. 如图,在矩形中,对角线 , 相交于点 , 点是边的中点,点在对角线上,且 , 连接 . 若 , 则 .
15. 如图,在矩形中,对角线 , 相交于点 , 点是边的中点,点在对角线上,且 , 连接 . 若 , 则 . 16. 如图,正方形ABCD的边长为8,点E是CD的中点,HG垂直平分AE且分别交AE、BC于点H、G,则BG=.
16. 如图,正方形ABCD的边长为8,点E是CD的中点,HG垂直平分AE且分别交AE、BC于点H、G,则BG=. 17. 如图,在 中, ,点D,E分别是 边上的中点,连接 .如果 , ,那么 的长是m.
17. 如图,在 中, ,点D,E分别是 边上的中点,连接 .如果 , ,那么 的长是m. 18. 如图,在矩形ABCD中, ,E,F分别是AD,AB的中点, 的平分线交AB于点G,点P是线段DG上的一个动点,则 的周长最小值为.
18. 如图,在矩形ABCD中, ,E,F分别是AD,AB的中点, 的平分线交AB于点G,点P是线段DG上的一个动点,则 的周长最小值为.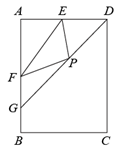 19. 如图,在正方形ABCD中, ,对角线 相交于点O.点E是对角线AC上一点,连接BE,过点E作 ,分别交 于点F、G,连接BF,交AC于点H,将 沿EF翻折,点H的对应点 恰好落在BD上,得到 若点F为CD的中点,则 的周长是.
19. 如图,在正方形ABCD中, ,对角线 相交于点O.点E是对角线AC上一点,连接BE,过点E作 ,分别交 于点F、G,连接BF,交AC于点H,将 沿EF翻折,点H的对应点 恰好落在BD上,得到 若点F为CD的中点,则 的周长是.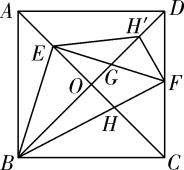 20. 如图,正方形中,点E、F分别在边上, , 则;若的面积等于1,则的值是.
20. 如图,正方形中,点E、F分别在边上, , 则;若的面积等于1,则的值是.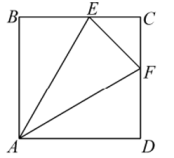 21. 如图,矩形的对角线 , 相交于点 , // , //.若 , 则四边形的周长是.
21. 如图,矩形的对角线 , 相交于点 , // , //.若 , 则四边形的周长是.
三、解答题
-
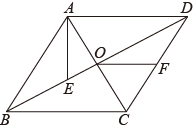
22. 如图,在 中,E,G,H,F分别是 上的点,且 .求证: .

四、综合题
-
23. 如图,在正方形中,为上一点,连接 , 的垂直平分线交于点 , 交于点 , 垂足为 , 点在上,且.
 (1)、求证:;(2)、若 , , 求的长.24. 如图,在中,交于点 , 点在上, .
(1)、求证:;(2)、若 , , 求的长.24. 如图,在中,交于点 , 点在上, .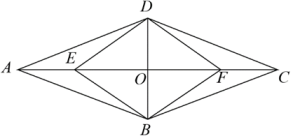 (1)、求证:四边形是平行四边形;(2)、若求证:四边形是菱形.25. 下面图片是八年级教科书中的一道题:如图,四边形是正方形,点是边的中点, , 且交正方形外角的平分线于点 . 求证 . (提示:取的中点 , 连接 . )
(1)、求证:四边形是平行四边形;(2)、若求证:四边形是菱形.25. 下面图片是八年级教科书中的一道题:如图,四边形是正方形,点是边的中点, , 且交正方形外角的平分线于点 . 求证 . (提示:取的中点 , 连接 . )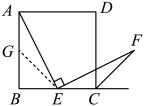 (1)、请你思考题中“提示”,这样添加辅助线的意图是得到条件:;(2)、如图1,若点是边上任意一点(不与、重合),其他条件不变.求证:;
(1)、请你思考题中“提示”,这样添加辅助线的意图是得到条件:;(2)、如图1,若点是边上任意一点(不与、重合),其他条件不变.求证:;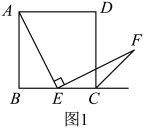 (3)、在(2)的条件下,连接 , 过点作 , 垂足为 . 设 , 当为何值时,四边形是平行四边形,并给予证明.26. 已知矩形的对角线相交于点O,点E是边上一点,连接 , 且 .
(3)、在(2)的条件下,连接 , 过点作 , 垂足为 . 设 , 当为何值时,四边形是平行四边形,并给予证明.26. 已知矩形的对角线相交于点O,点E是边上一点,连接 , 且 . (1)、如图1,求证:;(2)、如图2,设与相交于点F,与相交于点H,过点D作的平行线交的延长线于点G,在不添加任何辅助线的情况下,请直接写出图2中的四个三角形(除外),使写出的每个三角形的面积都与的面积相等.27. 如图,在中, , , . 动点从点出发,以的速度沿边向终点匀速运动.以为一边作 , 另一边与折线相交于点 , 以为边作菱形 , 点在线段上.设点的运动时间为 , 菱形与重叠部分图形的面积为 .
(1)、如图1,求证:;(2)、如图2,设与相交于点F,与相交于点H,过点D作的平行线交的延长线于点G,在不添加任何辅助线的情况下,请直接写出图2中的四个三角形(除外),使写出的每个三角形的面积都与的面积相等.27. 如图,在中, , , . 动点从点出发,以的速度沿边向终点匀速运动.以为一边作 , 另一边与折线相交于点 , 以为边作菱形 , 点在线段上.设点的运动时间为 , 菱形与重叠部分图形的面积为 .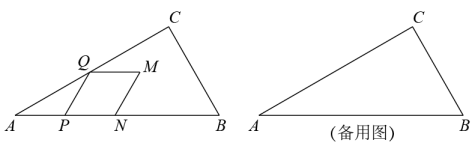 (1)、当点在边上时,的长为;(用含的代数式表示)(2)、当点落在边上时,求的值;(3)、求关于的函数解析式,并写出自变量的取值范围.28. 如图,在平行四边形中,是一条对角线,且 , , , 是边上两点,点在点的右侧, , 连接 , 的延长线与的延长线相交于点 .
(1)、当点在边上时,的长为;(用含的代数式表示)(2)、当点落在边上时,求的值;(3)、求关于的函数解析式,并写出自变量的取值范围.28. 如图,在平行四边形中,是一条对角线,且 , , , 是边上两点,点在点的右侧, , 连接 , 的延长线与的延长线相交于点 .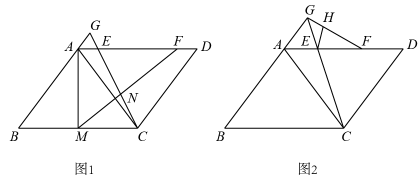 (1)、如图1,是边上一点,连接 , , 与相交于点 .
(1)、如图1,是边上一点,连接 , , 与相交于点 .①若 , 求的长;
②在满足①的条件下,若 , 求证:;
(2)、如图2,连接 , 是上一点,连接 . 若 , 且 , 求的长.29. 如图,已知四边形ABCD为矩形 , ,点E在BC上, ,将△ABC沿AC翻折到△AFC,连接EF. (1)、求EF的长;(2)、求sin∠CEF的值.30. 如图,在▱ABCD中,点O为对角线BD的中点,EF过点O且分别交AB、DC于点E、F,连接DE、BF.
(1)、求EF的长;(2)、求sin∠CEF的值.30. 如图,在▱ABCD中,点O为对角线BD的中点,EF过点O且分别交AB、DC于点E、F,连接DE、BF.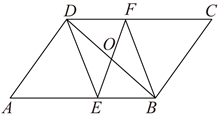
求证:
(1)、△DOF≌△BOE;(2)、DE=BF.31. 如图,在矩形 中, ,点E是 边上的任一点(不包括端点D,C),过点A作 交 的延长线于点F,设 .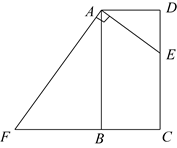 (1)、求 的长(用含a的代数式表示);(2)、连接 交 于点G,连接 ,当 时,求证:四边形 是菱形.32. 如图,在平行四边形ABCD中,点E,F分别在AD,BC上,且 ,连接AF,CE,AC,EF,且AC与EF相交于点O.
(1)、求 的长(用含a的代数式表示);(2)、连接 交 于点G,连接 ,当 时,求证:四边形 是菱形.32. 如图,在平行四边形ABCD中,点E,F分别在AD,BC上,且 ,连接AF,CE,AC,EF,且AC与EF相交于点O.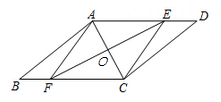 (1)、求证:四边形AFCE是平行四边形;(2)、若AC平分 , ,求四边形AFCE的面积.33. 如图,在 中,BD是它的一条对角线,
(1)、求证:四边形AFCE是平行四边形;(2)、若AC平分 , ,求四边形AFCE的面积.33. 如图,在 中,BD是它的一条对角线,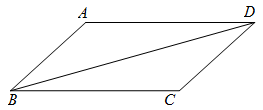 (1)、求证: ;(2)、尺规作图:作BD的垂直平分线EF,分别交AD,BC于点E,F(不写作法,保留作图痕迹);(3)、连接BE,若 ,求 的度数.34. 阅读材料:小明喜欢探究数学问题,一天杨老师给他这样一个几何问题:
(1)、求证: ;(2)、尺规作图:作BD的垂直平分线EF,分别交AD,BC于点E,F(不写作法,保留作图痕迹);(3)、连接BE,若 ,求 的度数.34. 阅读材料:小明喜欢探究数学问题,一天杨老师给他这样一个几何问题:如图,和都是等边三角形,点在上.
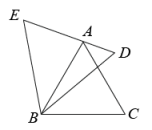
求证:以、、为边的三角形是钝角三角形.
(1)、【探究发现】小明通过探究发现:连接 , 根据已知条件,可以证明 , , 从而得出为钝角三角形,故以、、为边的三角形是钝角三角形.请你根据小明的思路,写出完整的证明过程.
(2)、【拓展迁移】如图,四边形和四边形都是正方形,点在上.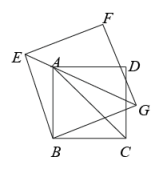
①试猜想:以、、为边的三角形的形状,并说明理由.
②若 , 试求出正方形的面积.
35. 如图,点 , 分别在的边 , 上, , 连接 , .请从以下三个条件:①;②;③中,选择一个合适的作为已知条件,使为菱形.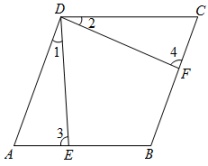 (1)、你添加的条件是(填序号);(2)、添加了条件后,请证明为菱形.36. 如图,在中,对角线AC,BD相交于点O,.
(1)、你添加的条件是(填序号);(2)、添加了条件后,请证明为菱形.36. 如图,在中,对角线AC,BD相交于点O,. (1)、求证:;(2)、若点E,F分别为AD,AO的中点,连接EF, , 求BD的长及四边形ABCD的周长.37. 如图1,矩形中, , 点P在边上,且不与点B、C重合,直线与的延长线交于点E.
(1)、求证:;(2)、若点E,F分别为AD,AO的中点,连接EF, , 求BD的长及四边形ABCD的周长.37. 如图1,矩形中, , 点P在边上,且不与点B、C重合,直线与的延长线交于点E.
 (1)、当点P是的中点时,求证:;(2)、将沿直线折叠得到 , 点落在矩形的内部,延长交直线于点F.
(1)、当点P是的中点时,求证:;(2)、将沿直线折叠得到 , 点落在矩形的内部,延长交直线于点F.①证明 , 并求出在(1)条件下的值;
②连接 , 求周长的最小值;
③如图2,交于点H,点G是的中点,当时,请判断与的数量关系,并说明理由.
38. 如图,BD是矩形ABCD的对角线.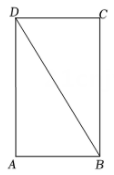 (1)、求作⊙A,使得⊙A与BD相切(要求:尺规作图,不写作法,保留作图痕迹);(2)、在(1)的条件下,设BD与⊙A相切于点E,CF⊥BD,垂足为F.若直线CF与⊙A相切于点G,求的值.
(1)、求作⊙A,使得⊙A与BD相切(要求:尺规作图,不写作法,保留作图痕迹);(2)、在(1)的条件下,设BD与⊙A相切于点E,CF⊥BD,垂足为F.若直线CF与⊙A相切于点G,求的值.
-