2022年全国中考数学真题分类汇编19 四边形及多边形(3)
试卷更新日期:2022-12-29 类型:二轮复习
一、单选题
-
1. 如图,在边长为1的菱形中, , 动点E在边上(与点A、B均不重合),点F在对角线上,与相交于点G,连接 , 若 , 则下列结论错误的是( )
 A、 B、 C、 D、的最小值为2. 要检验一个四边形的桌面是否为矩形,可行的测量方案是( )A、测量两条对角线是否相等 B、度量两个角是否是90° C、测量两条对角线的交点到四个顶点的距离是否相等 D、测量两组对边是否分别相等3. 如图,已知菱形的边长为2,对角线相交于点O,点M,N分别是边上的动点, , 连接.以下四个结论正确的是( )
A、 B、 C、 D、的最小值为2. 要检验一个四边形的桌面是否为矩形,可行的测量方案是( )A、测量两条对角线是否相等 B、度量两个角是否是90° C、测量两条对角线的交点到四个顶点的距离是否相等 D、测量两组对边是否分别相等3. 如图,已知菱形的边长为2,对角线相交于点O,点M,N分别是边上的动点, , 连接.以下四个结论正确的是( )
①是等边三角形;②的最小值是;③当最小时;④当时,.
A、①②③ B、①②④ C、①③④ D、①②③④4. 如图,菱形ABCD的边长为2,点P是对角线AC上的一个动点,点E、F分别为边AD、DC的中点,则PE + PF的最小值是( ) A、2 B、 C、1.5 D、5. 如图,“赵爽弦图”是由四个全等的直角三角形与中间的一个小正方形拼成的大正方形,若图中的直角三角形的两条直角边的长分别为1和3,则中间小正方形的周长是( )
A、2 B、 C、1.5 D、5. 如图,“赵爽弦图”是由四个全等的直角三角形与中间的一个小正方形拼成的大正方形,若图中的直角三角形的两条直角边的长分别为1和3,则中间小正方形的周长是( ) A、4 B、8 C、12 D、166. 下列说法正确的是( )A、对角线相等的四边形是矩形. B、相似三角形的面积的比等于相似比. C、方差越大,数据的波动越大;方差越小,数据的波动越小. D、过一点有且只有一条直线与已知直线平行.7. 如图,将菱形纸片沿着线段剪成两个全等的图形,则的度数是( )
A、4 B、8 C、12 D、166. 下列说法正确的是( )A、对角线相等的四边形是矩形. B、相似三角形的面积的比等于相似比. C、方差越大,数据的波动越大;方差越小,数据的波动越小. D、过一点有且只有一条直线与已知直线平行.7. 如图,将菱形纸片沿着线段剪成两个全等的图形,则的度数是( ) A、40° B、60° C、80° D、100°8. 如图,在▱ABCD中,已知AB=12,AD=8,∠ABC的平分线BM交CD边于点M,则DM的长为( )
A、40° B、60° C、80° D、100°8. 如图,在▱ABCD中,已知AB=12,AD=8,∠ABC的平分线BM交CD边于点M,则DM的长为( )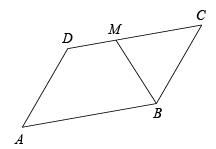 A、2 B、4 C、6 D、89. 由4个形状相同,大小相等的菱形组成如图所示的网格,菱形的顶点称为格点,点A,B,C都在格点上,∠O=60°,则tan∠ABC=( )
A、2 B、4 C、6 D、89. 由4个形状相同,大小相等的菱形组成如图所示的网格,菱形的顶点称为格点,点A,B,C都在格点上,∠O=60°,则tan∠ABC=( ) A、 B、 C、 D、10. 如图,在矩形ABCD中,连接BD,分别以B、D为圆心,大于的长为半径画弧,两弧交于P、Q两点,作直线PQ,分别与AD、BC交于点M、N,连接BM、DN.若 , .则四边形MBND的周长为( )
A、 B、 C、 D、10. 如图,在矩形ABCD中,连接BD,分别以B、D为圆心,大于的长为半径画弧,两弧交于P、Q两点,作直线PQ,分别与AD、BC交于点M、N,连接BM、DN.若 , .则四边形MBND的周长为( ) A、 B、5 C、10 D、20
A、 B、5 C、10 D、20二、填空题
-
11. 如图,在正方形中,点为的中点, , 交于点 , 于点 , 平分 , 分别交 , 于点 , , 延长交于点 , 连接 . 下列结论:①;②;③;④ . 其中正确的是 . (填序号即可).
 12. 如图,菱形的边长为2, , 对角线与交于点 , 为中点,为中点,连接 , 则的长为 .
12. 如图,菱形的边长为2, , 对角线与交于点 , 为中点,为中点,连接 , 则的长为 .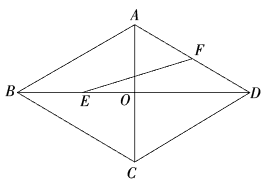 13. 如图,在正方形中,E为的中点,连接交于点F.若 , 则的面积为 .
13. 如图,在正方形中,E为的中点,连接交于点F.若 , 则的面积为 .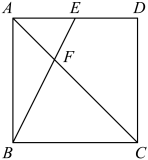 14. 如图,在矩形ABCD中,AD=2 , DC=4 , 将线段DC绕点D按逆时针方向旋转,当点C的对应点E恰好落在边AB上时,图中阴影部分的面积是 .
14. 如图,在矩形ABCD中,AD=2 , DC=4 , 将线段DC绕点D按逆时针方向旋转,当点C的对应点E恰好落在边AB上时,图中阴影部分的面积是 .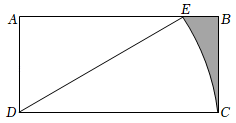 15. 勾股定理被记载于我国古代的数学著作《周髀算经》中,汉代数学家赵爽为了证明勾股定理,创制了一幅如图①所示的“弦图”,后人称之为“赵爽弦图”.图②由弦图变化得到,它是由八个全等的直角三角形拼接而成.记图中正方形ABCD、正方形EFGH、正方形MNKT的面积分别为S1、S2、S3.若正方形EFGH的边长为4,则S1+S2+S3=.
15. 勾股定理被记载于我国古代的数学著作《周髀算经》中,汉代数学家赵爽为了证明勾股定理,创制了一幅如图①所示的“弦图”,后人称之为“赵爽弦图”.图②由弦图变化得到,它是由八个全等的直角三角形拼接而成.记图中正方形ABCD、正方形EFGH、正方形MNKT的面积分别为S1、S2、S3.若正方形EFGH的边长为4,则S1+S2+S3=. 16. 如图,矩形ABCD中,AB=6,AD=4,点E、F分别是AB、DC上的动点,EF∥BC,则AF+CE的最小值是 .
16. 如图,矩形ABCD中,AB=6,AD=4,点E、F分别是AB、DC上的动点,EF∥BC,则AF+CE的最小值是 .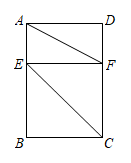 17. 如图,将一个边长为的正方形活动框架(边框粗细忽略不计)扭动成四边形 , 对角线是两根橡皮筋,其拉伸长度达到时才会断裂.若 , 则橡皮筋断裂(填“会”或“不会”,参考数据:).
17. 如图,将一个边长为的正方形活动框架(边框粗细忽略不计)扭动成四边形 , 对角线是两根橡皮筋,其拉伸长度达到时才会断裂.若 , 则橡皮筋断裂(填“会”或“不会”,参考数据:).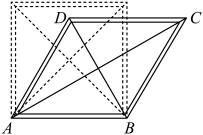 18. 如图,在四边形中, , 平分.若 , , 则.
18. 如图,在四边形中, , 平分.若 , , 则.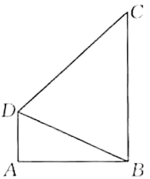 19. 如图,四边形ABCD为菱形,∠ABC=80°,延长BC到E,在∠DCE内作射钱CM,使得∠ECM=30°,过点D作DF⊥CM,垂足为F.若DF= , 则BD的长为(结果保留很号).
19. 如图,四边形ABCD为菱形,∠ABC=80°,延长BC到E,在∠DCE内作射钱CM,使得∠ECM=30°,过点D作DF⊥CM,垂足为F.若DF= , 则BD的长为(结果保留很号).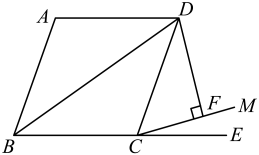 20. 如图,在边长为2的正方形ABCD中,点E为AD的中点,将△CDE沿CE翻折得△CME,点M落在四边形ABCE内.点N为线段CE上的动点,过点N作NP//EM交MC于点P,则MN+NP的最小值为.
20. 如图,在边长为2的正方形ABCD中,点E为AD的中点,将△CDE沿CE翻折得△CME,点M落在四边形ABCE内.点N为线段CE上的动点,过点N作NP//EM交MC于点P,则MN+NP的最小值为.
 21. 正六边形一个外角的度数为.22. 如图,把一张矩形纸片沿对角线折叠,若BC=9,CD=3,那么阴影部分的面积为 .
21. 正六边形一个外角的度数为.22. 如图,把一张矩形纸片沿对角线折叠,若BC=9,CD=3,那么阴影部分的面积为 .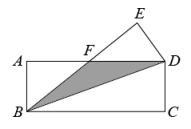
三、作图题
-
23. 已知四边形为矩形.点E是边的中点.请仅用无刻度的直尺完成下列作图,不写作法,保留作图痕迹.
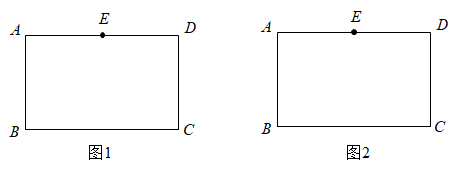 (1)、在图1中作出矩形的对称轴m,使;(2)、在图2中作出矩形的对称轴n:使.
(1)、在图1中作出矩形的对称轴m,使;(2)、在图2中作出矩形的对称轴n:使.四、解答题
-
24. 如图,在四边形中,与交于点 , , , 垂足分别为点 , , 且 , . 求证:四边形是平行四边形.
 25. 如图,已知四边形ABCD是正方形,G为线段AD上任意一点,于点E,于点F.求证:.
25. 如图,已知四边形ABCD是正方形,G为线段AD上任意一点,于点E,于点F.求证:.
五、综合题
-
26. 如图,在Rt中, , . 点D是的中点,过点D作交于点E.延长至点F,使得 , 连接、、 .
 (1)、求证:四边形是菱形;(2)、若 , 则的值为 .27. 如图,在中, , , 点M为边的中点,动点P从点A出发,沿折线以每秒个单位长度的速度向终点B运动,连结 . 作点A关于直线的对称点 , 连结、 . 设点P的运动时间为t秒.
(1)、求证:四边形是菱形;(2)、若 , 则的值为 .27. 如图,在中, , , 点M为边的中点,动点P从点A出发,沿折线以每秒个单位长度的速度向终点B运动,连结 . 作点A关于直线的对称点 , 连结、 . 设点P的运动时间为t秒. (1)、点D到边的距离为;(2)、用含t的代数式表示线段的长;(3)、连结 , 当线段最短时,求的面积;(4)、当M、、C三点共线时,直接写出t的值.28. 【探索发现】在一次折纸活动中,小亮同学选用了常见的A4纸,如图①,矩形为它的示意图.他查找了A4纸的相关资料,根据资料显示得出图①中 . 他先将A4纸沿过点A的直线折叠,使点B落在上,点B的对应点为点E,折痕为;再沿过点F的直线折叠,使点C落在上,点C的对应点为点H,折痕为;然后连结 , 沿所在的直线再次折叠,发现点D与点F重合,进而猜想 .
(1)、点D到边的距离为;(2)、用含t的代数式表示线段的长;(3)、连结 , 当线段最短时,求的面积;(4)、当M、、C三点共线时,直接写出t的值.28. 【探索发现】在一次折纸活动中,小亮同学选用了常见的A4纸,如图①,矩形为它的示意图.他查找了A4纸的相关资料,根据资料显示得出图①中 . 他先将A4纸沿过点A的直线折叠,使点B落在上,点B的对应点为点E,折痕为;再沿过点F的直线折叠,使点C落在上,点C的对应点为点H,折痕为;然后连结 , 沿所在的直线再次折叠,发现点D与点F重合,进而猜想 .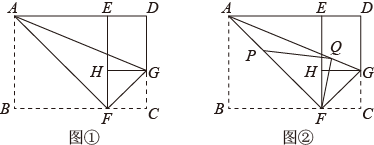 (1)、【问题解决】
(1)、【问题解决】小亮对上面的猜想进行了证明,下面是部分证明过程:
证明:四边形是矩形,
∴ .
由折叠可知, , .
∴ .
∴ .
请你补全余下的证明过程.
(2)、【结论应用】的度数为度,的值为;
(3)、在图①的条件下,点P在线段上,且 , 点Q在线段上,连结、 , 如图②,设 , 则的最小值为 . (用含a的代数式表示)29. 已知点在正方形的对角线上,正方形与正方形有公共点 .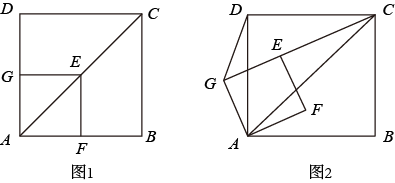 (1)、如图1,当点在上,在上,求的值为多少;(2)、将正方形绕点逆时针方向旋转 , 如图2,求:的值为多少;(3)、 , , 将正方形绕逆时针方向旋转 , 当 , , 三点共线时,请直接写出的长度.30. 和均为等边三角形,点E、D分别从点A,B同时出发,以相同的速度沿运动,运动到点B、C停止.
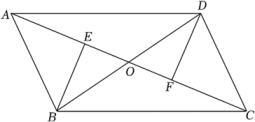
(1)、如图1,当点在上,在上,求的值为多少;(2)、将正方形绕点逆时针方向旋转 , 如图2,求:的值为多少;(3)、 , , 将正方形绕逆时针方向旋转 , 当 , , 三点共线时,请直接写出的长度.30. 和均为等边三角形,点E、D分别从点A,B同时出发,以相同的速度沿运动,运动到点B、C停止.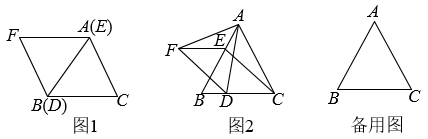 (1)、如图1,当点E、D分别与点A、B重合时,请判断:线段的数量关系是 , 位置关系是;(2)、如图2,当点E、D不与点A,B重合时,(1)中的结论是否依然成立?若成立,请给予证明;若不成立,请说明理由;(3)、当点D运动到什么位置时,四边形的面积是面积的一半,请直接写出答案;此时,四边形是哪种特殊四边形?请在备用图中画出图形并给予证明.31. 如图,中,E、F是对角线BD上两个点,且满足BE=DF.
(1)、如图1,当点E、D分别与点A、B重合时,请判断:线段的数量关系是 , 位置关系是;(2)、如图2,当点E、D不与点A,B重合时,(1)中的结论是否依然成立?若成立,请给予证明;若不成立,请说明理由;(3)、当点D运动到什么位置时,四边形的面积是面积的一半,请直接写出答案;此时,四边形是哪种特殊四边形?请在备用图中画出图形并给予证明.31. 如图,中,E、F是对角线BD上两个点,且满足BE=DF.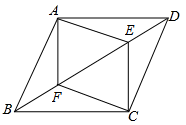 (1)、求证:△ABE≌△CDF;(2)、求证:四边形AECF是平行四边形.32. 如图,在矩形ABCD中,AB=6,BC=4,点M、N分别在AB、AD上,且MN⊥MC,点E为CD的中点,连接BE交MC于点F.
(1)、求证:△ABE≌△CDF;(2)、求证:四边形AECF是平行四边形.32. 如图,在矩形ABCD中,AB=6,BC=4,点M、N分别在AB、AD上,且MN⊥MC,点E为CD的中点,连接BE交MC于点F. (1)、当F为BE的中点时,求证:AM=CE;(2)、若=2,求的值;(3)、若MN∥BE,求的值.33. 小红根据学习轴对称的经验,对线段之间、角之间的关系进行了拓展探究.
(1)、当F为BE的中点时,求证:AM=CE;(2)、若=2,求的值;(3)、若MN∥BE,求的值.33. 小红根据学习轴对称的经验,对线段之间、角之间的关系进行了拓展探究.如图,在中,为边上的高, , 点在边上,且 , 点是线段上任意一点,连接 , 将沿翻折得.
 (1)、问题解决:
(1)、问题解决:如图①,当 , 将沿翻折后,使点与点重合,则;
(2)、问题探究:如图②,当 , 将沿翻折后,使 , 求的度数,并求出此时的最小值;
(3)、拓展延伸:当 , 将沿翻折后,若 , 且 , 根据题意在备用图中画出图形,并求出的值.
34. 在四边形中,是边上的一点.若 , 则点叫做该四边形的“等形点”.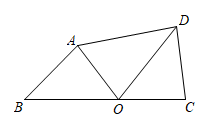 (1)、正方形“等形点”(填“存在”或“不存在”);(2)、如图,在四边形中,边上的点是四边形的“等形点”.已知 , , , 连接 , 求的长;(3)、在四边形中,EH//FG.若边上的点是四边形的“等形点”,求的值.35. 如图,在四边形中,对角线与相交于点O,记的面积为 , 的面积为.
(1)、正方形“等形点”(填“存在”或“不存在”);(2)、如图,在四边形中,边上的点是四边形的“等形点”.已知 , , , 连接 , 求的长;(3)、在四边形中,EH//FG.若边上的点是四边形的“等形点”,求的值.35. 如图,在四边形中,对角线与相交于点O,记的面积为 , 的面积为. (1)、问题解决:如图①,若AB//CD,求证:(2)、探索推广:如图②,若与不平行,(1)中的结论是否成立?若成立,请证明;若不成立,请说明理由.(3)、拓展应用:如图③,在上取一点E,使 , 过点E作交于点F,点H为的中点,交于点G,且 , 若 , 求值.36. 如图,线段DE与AF分别为△ABC的中位线与中线.
(1)、问题解决:如图①,若AB//CD,求证:(2)、探索推广:如图②,若与不平行,(1)中的结论是否成立?若成立,请证明;若不成立,请说明理由.(3)、拓展应用:如图③,在上取一点E,使 , 过点E作交于点F,点H为的中点,交于点G,且 , 若 , 求值.36. 如图,线段DE与AF分别为△ABC的中位线与中线.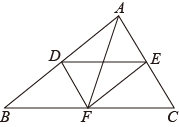 (1)、求证:AF与DE互相平分;(2)、当线段AF与BC满足怎样的数量关系时,四边形ADFE为矩形?请说明理由.37. 如图,E,F是正方形ABCD的对角线BD上的两点,且BE=DF.
(1)、求证:AF与DE互相平分;(2)、当线段AF与BC满足怎样的数量关系时,四边形ADFE为矩形?请说明理由.37. 如图,E,F是正方形ABCD的对角线BD上的两点,且BE=DF.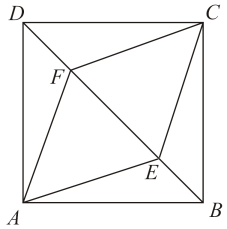 (1)、求证:△ABE≌△CDF;(2)、若AB=3 , BE=2,求四边形AECF的面积.38. 如图,在平行四边形ABCD中,点E和点F是对角线BD上的两点,且BF=DE.
(1)、求证:△ABE≌△CDF;(2)、若AB=3 , BE=2,求四边形AECF的面积.38. 如图,在平行四边形ABCD中,点E和点F是对角线BD上的两点,且BF=DE.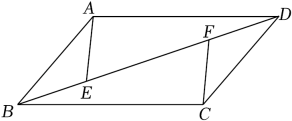 (1)、求证:BE=DF;(2)、求证:ABE≌CDF.39. 将正方形和菱形按照如图所示摆放,顶点D与顶点H重合,菱形的对角线经过点B,点E,G分别在 , 上.
(1)、求证:BE=DF;(2)、求证:ABE≌CDF.39. 将正方形和菱形按照如图所示摆放,顶点D与顶点H重合,菱形的对角线经过点B,点E,G分别在 , 上.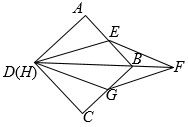 (1)、求证:;(2)、若 , 求的长.40. 同学们还记得吗?图①、图②是人教版八年级下册教材“实验与探究”中我们研究过的两个图形.受这两个图形的启发,数学兴趣小组提出了以下三个问题,请你回答:
(1)、求证:;(2)、若 , 求的长.40. 同学们还记得吗?图①、图②是人教版八年级下册教材“实验与探究”中我们研究过的两个图形.受这两个图形的启发,数学兴趣小组提出了以下三个问题,请你回答: (1)、【问题一】如图①,正方形的对角线相交于点 , 点又是正方形的一个顶点,交于点 , 交于点 , 则与的数量关系为;(2)、【问题二】受图①启发,兴趣小组画出了图③:直线、经过正方形的对称中心 , 直线分别与、交于点、 , 直线分别与、交于点、 , 且 , 若正方形边长为8,求四边形的面积;
(1)、【问题一】如图①,正方形的对角线相交于点 , 点又是正方形的一个顶点,交于点 , 交于点 , 则与的数量关系为;(2)、【问题二】受图①启发,兴趣小组画出了图③:直线、经过正方形的对称中心 , 直线分别与、交于点、 , 直线分别与、交于点、 , 且 , 若正方形边长为8,求四边形的面积; (3)、【问题三】受图②启发,兴趣小组画出了图④:正方形的顶点在正方形的边上,顶点在的延长线上,且 , . 在直线上是否存在点 , 使为直角三角形?若存在,求出的长度;若不存在,说明理由.
(3)、【问题三】受图②启发,兴趣小组画出了图④:正方形的顶点在正方形的边上,顶点在的延长线上,且 , . 在直线上是否存在点 , 使为直角三角形?若存在,求出的长度;若不存在,说明理由.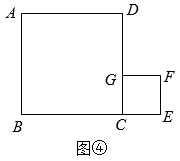
-