2022年全国中考数学真题分类汇编19 四边形及多边形(2)
试卷更新日期:2022-12-29 类型:二轮复习
一、单选题
-
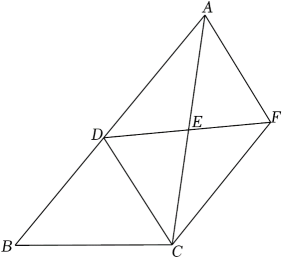
1. 如图,在菱形中,分别以、为圆心,大于为半径画弧,两弧分别交于点、 , 连接 , 若直线恰好过点与边交于点 , 连接 , 则下列结论错误的是( )
 A、 B、若 , 则 C、 D、2. 如图1,在菱形ABCD中,∠C=120°,M是AB的中点,N是对角线BD上一动点,设DN长为x,线段MN与AN长度的和为y,图2是y关于x的函数图象,图象右端点F的坐标为 , 则图象最低点E的坐标为( )
A、 B、若 , 则 C、 D、2. 如图1,在菱形ABCD中,∠C=120°,M是AB的中点,N是对角线BD上一动点,设DN长为x,线段MN与AN长度的和为y,图2是y关于x的函数图象,图象右端点F的坐标为 , 则图象最低点E的坐标为( )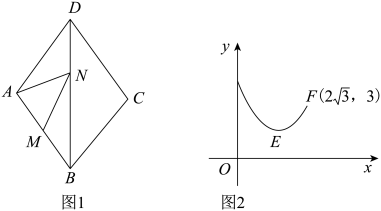 A、 B、 C、 D、3. 如图,菱形ABCD的对角线AC与BD相交于点O,E为AD的中点,连接OE, , ,则 ( )
A、 B、 C、 D、3. 如图,菱形ABCD的对角线AC与BD相交于点O,E为AD的中点,连接OE, , ,则 ( )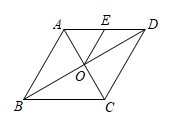 A、4 B、 C、2 D、4. 如图,四边形 的内角和等于( )
A、4 B、 C、2 D、4. 如图,四边形 的内角和等于( ) A、 B、 C、 D、5. 如图所示,将一矩形纸片沿AB折叠,已知 , 则( )
A、 B、 C、 D、5. 如图所示,将一矩形纸片沿AB折叠,已知 , 则( )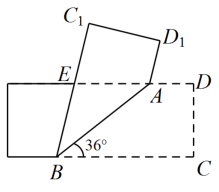 A、48° B、66° C、72° D、78°6. 如图,菱形ABCD中,AB=2 , ∠ABC=60°,矩形BEFG的边EF经过点C,且点G在边AD上,若BG=4,则BE的长为( )
A、48° B、66° C、72° D、78°6. 如图,菱形ABCD中,AB=2 , ∠ABC=60°,矩形BEFG的边EF经过点C,且点G在边AD上,若BG=4,则BE的长为( )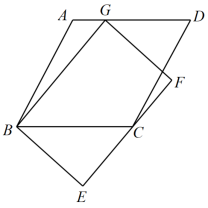 A、 B、 C、 D、37. 如图,在菱形ABCD中, , M是对角线BD上的一个动点, , 则的最小值为( )
A、 B、 C、 D、37. 如图,在菱形ABCD中, , M是对角线BD上的一个动点, , 则的最小值为( )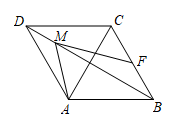 A、1 B、 C、 D、28. 如图,矩形ABCD中,分别以A,C为圆心,以大于的长为半径作弧,两弧相交于M,N两点,作直线MN分别交AD,BC于点E,F,连接AF,若BF=3,AE=5,以下结论错误的是( )
A、1 B、 C、 D、28. 如图,矩形ABCD中,分别以A,C为圆心,以大于的长为半径作弧,两弧相交于M,N两点,作直线MN分别交AD,BC于点E,F,连接AF,若BF=3,AE=5,以下结论错误的是( )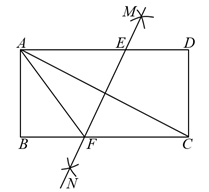 A、AF=CF B、∠FAC=∠EAC C、AB=4 D、AC=2AB9. 如图,正方形ABCD的面积为3,点E在边CD上, 且CE = 1,∠ABE的平分线交AD于点F,点M,N分别是BE,BF的中点,则MN的长为( )
A、AF=CF B、∠FAC=∠EAC C、AB=4 D、AC=2AB9. 如图,正方形ABCD的面积为3,点E在边CD上, 且CE = 1,∠ABE的平分线交AD于点F,点M,N分别是BE,BF的中点,则MN的长为( )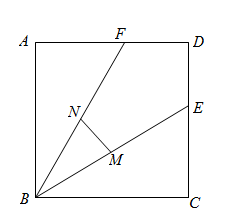 A、 B、 C、 D、10. 如图,在菱形ABCD中,对角线AC,BD相交于点O,下列结论中错误的是( )
A、 B、 C、 D、10. 如图,在菱形ABCD中,对角线AC,BD相交于点O,下列结论中错误的是( ) A、AB=AD B、AC⊥BD C、AC=BD D、∠DAC=∠BAC11. 下列说法错误的是( )A、对角线垂直且互相平分的四边形是菱形 B、同圆或等圆中,同弧对应的圆周角相等 C、对角线相等的四边形是矩形 D、对角线垂直且相等的平行四边形是正方形
A、AB=AD B、AC⊥BD C、AC=BD D、∠DAC=∠BAC11. 下列说法错误的是( )A、对角线垂直且互相平分的四边形是菱形 B、同圆或等圆中,同弧对应的圆周角相等 C、对角线相等的四边形是矩形 D、对角线垂直且相等的平行四边形是正方形二、填空题
-
12. 一个正n边形的一个外角等于36°,则n= .13. 如图,中, , , 点 , 分别是 , 的中点,点在上,且 , 则EF= .
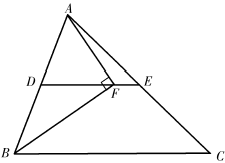 14. 如图,在矩形纸片ABCD中,点E在BC边上,将 沿DE翻折得到 ,点F落在AE上.若 , ,则 cm.
14. 如图,在矩形纸片ABCD中,点E在BC边上,将 沿DE翻折得到 ,点F落在AE上.若 , ,则 cm.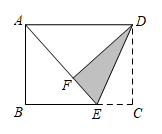 15. 如图,在矩形ABCD中,按以下步骤作图:①分别以点B和D为圆心,以大于BD的长为半径作弧,两弧相交于点E和F;②作直线EF分别与DC,DB,AB交于点M,O,N.若DM=5,CM=3,则MN= .
15. 如图,在矩形ABCD中,按以下步骤作图:①分别以点B和D为圆心,以大于BD的长为半径作弧,两弧相交于点E和F;②作直线EF分别与DC,DB,AB交于点M,O,N.若DM=5,CM=3,则MN= . 16. 如图,四边形ABCD是边长为6的菱形,∠ABC=60°,对角线AC与BD交于点O,点E,F分别是线段AB,AC上的动点(不与端点重合),且BE=AF,BF与CE交于点P,延长BF交边AD(或边CD)于点G,连接OP,OG,则下列结论:①△ABF≌△BCE;②当BE=2时,△BOG的面积与四边形OCDG面积之比为1:3;③当BE=4时,BE:CG=2:1;④线段OP的最小值为2﹣2 . 其中正确的是 . (请填写序号)
16. 如图,四边形ABCD是边长为6的菱形,∠ABC=60°,对角线AC与BD交于点O,点E,F分别是线段AB,AC上的动点(不与端点重合),且BE=AF,BF与CE交于点P,延长BF交边AD(或边CD)于点G,连接OP,OG,则下列结论:①△ABF≌△BCE;②当BE=2时,△BOG的面积与四边形OCDG面积之比为1:3;③当BE=4时,BE:CG=2:1;④线段OP的最小值为2﹣2 . 其中正确的是 . (请填写序号) 17. 如果正n边形的一个内角与一个外角的比是3:2,则 .18. 利用图形的分、和、移、补探索图形关系,是我国传统数学的一种重要方法.如图1,BD是矩形ABCD的对角线,将△BCD分割成两对全等的直角三角形和一个正方形,然后按图2重新摆放,观察两图,若a=4,b=2,则矩形ABCD的面积是 .
17. 如果正n边形的一个内角与一个外角的比是3:2,则 .18. 利用图形的分、和、移、补探索图形关系,是我国传统数学的一种重要方法.如图1,BD是矩形ABCD的对角线,将△BCD分割成两对全等的直角三角形和一个正方形,然后按图2重新摆放,观察两图,若a=4,b=2,则矩形ABCD的面积是 . 19. 如图,在矩形ABCD中,BC=2AB,点P为边AD上的一个动点,线段BP绕点B顺时针旋转60°得到线段BP',连接PP' ,CP'.当点P' 落在边BC上时,∠PP'C的度数为; 当线段CP' 的长度最小时,∠PP'C的度数为
19. 如图,在矩形ABCD中,BC=2AB,点P为边AD上的一个动点,线段BP绕点B顺时针旋转60°得到线段BP',连接PP' ,CP'.当点P' 落在边BC上时,∠PP'C的度数为; 当线段CP' 的长度最小时,∠PP'C的度数为 20. 如图,在▱ABCD中,AD=10,对角线AC 与BD相交于点O,AC+BD=22,则△BOC的周长为
20. 如图,在▱ABCD中,AD=10,对角线AC 与BD相交于点O,AC+BD=22,则△BOC的周长为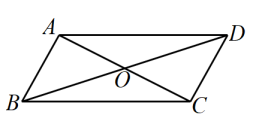 21. 如图,对折矩形纸片 , 使得与重合,得到折痕 , 把纸片展平,再一次折叠纸片,使点A的对应点落在上,并使折痕经过点B,得到折痕 . 连接 , 若 , , 则的长是 .
21. 如图,对折矩形纸片 , 使得与重合,得到折痕 , 把纸片展平,再一次折叠纸片,使点A的对应点落在上,并使折痕经过点B,得到折痕 . 连接 , 若 , , 则的长是 .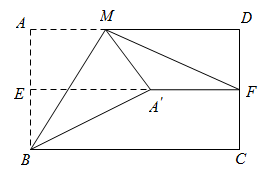 22. 如图矩形ABCD的对角线AC和BD相交于点O,过点O的直线分别交AD和BC于点E,F,AB=3,BC=4,则图中阴影部分的面积为 .
22. 如图矩形ABCD的对角线AC和BD相交于点O,过点O的直线分别交AD和BC于点E,F,AB=3,BC=4,则图中阴影部分的面积为 . 23. 如图,把边长为1:2的矩形ABCD沿长边BC,AD的中点E,F对折,得到四边形ABEF,点G,H分别在BE,EF上,且BG=EH=BE=2,AG与BH交于点O,N为AF的中点,连接ON,作OM⊥ON交AB于点M,连接MN,则tan∠AMN=.
23. 如图,把边长为1:2的矩形ABCD沿长边BC,AD的中点E,F对折,得到四边形ABEF,点G,H分别在BE,EF上,且BG=EH=BE=2,AG与BH交于点O,N为AF的中点,连接ON,作OM⊥ON交AB于点M,连接MN,则tan∠AMN=.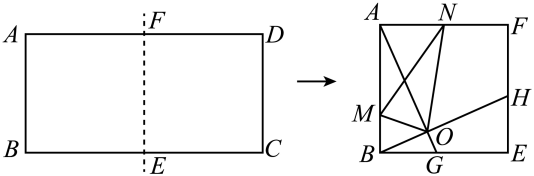 24. 如图,四边形为矩形, , 点E为边上一点,将沿翻折,点C的对应点为点F,过点F作的平行线交于点G,交直线于点H.若点G是边的三等分点,则的长是 .
24. 如图,四边形为矩形, , 点E为边上一点,将沿翻折,点C的对应点为点F,过点F作的平行线交于点G,交直线于点H.若点G是边的三等分点,则的长是 . 25. 如图,在直角坐标系中,边长为2个单位长度的正方形绕原点O逆时针旋转 , 再沿y轴方向向上平移1个单位长度,则点的坐标为 .
25. 如图,在直角坐标系中,边长为2个单位长度的正方形绕原点O逆时针旋转 , 再沿y轴方向向上平移1个单位长度,则点的坐标为 .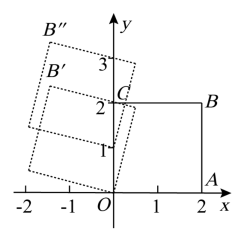
三、解答题
-
26. 已知:如图,在菱形ABCD中,E,F是对角线AC上两点,连接DE,DF,∠ADF=∠CDE.求证:AE=CF.
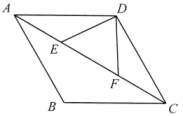 27. 如图,四边形是菱形,点E,F分别在上, . 求证 .
27. 如图,四边形是菱形,点E,F分别在上, . 求证 .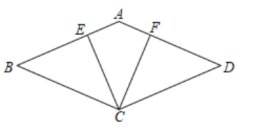 28. 如图,四边形ABCD是菱形,E,F是对角线AC上的两点,且 ,连接BF.FD,DE,EB.
28. 如图,四边形ABCD是菱形,E,F是对角线AC上的两点,且 ,连接BF.FD,DE,EB.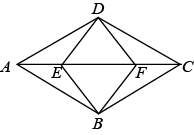
求证:四边形DEBF是菱形.
29. 如图,在▱ABCD中,DF平分∠ADC,交AB于点F,BEDF,交AD的延长线于点E.若∠A=40°,求∠ABE的度数.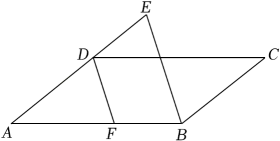
四、综合题
-
30. 如图,在中,AD是的角平分线,分别以点A,D为圆心,大于的长为半径作弧,两弧交于点M,N,作直线MN,分别交AB,AD,AC于点E,O,F,连接DE,DF.
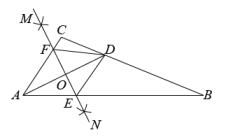 (1)、由作图可知,直线MN是线段AD的 .(2)、求证:四边形AEDF是菱形.31. 如图1,△ABC是等腰直角三角形,AC=BC=4,∠C=90°,M,N分别是边AC,BC上的点,以CM,CN为邻边作矩形PMCN,交AB于E,F.设CM=a,CN=b,若ab=8.
(1)、由作图可知,直线MN是线段AD的 .(2)、求证:四边形AEDF是菱形.31. 如图1,△ABC是等腰直角三角形,AC=BC=4,∠C=90°,M,N分别是边AC,BC上的点,以CM,CN为邻边作矩形PMCN,交AB于E,F.设CM=a,CN=b,若ab=8.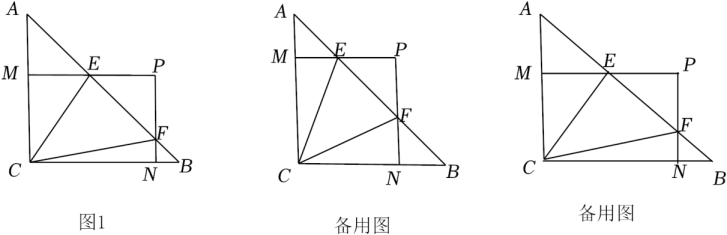 (1)、判断由线段AE,EF,BF组成的三角形的形状,并说明理由;(2)、①当a=b时,求∠ECF的度数;
(1)、判断由线段AE,EF,BF组成的三角形的形状,并说明理由;(2)、①当a=b时,求∠ECF的度数;②当a≠b时,①中的结论是否成立?并说明理由.
32. 在平面直角坐标系中, 是第一象限内一点,给出如下定义: 和 两个值中的最大值叫做点P的“倾斜系数”k.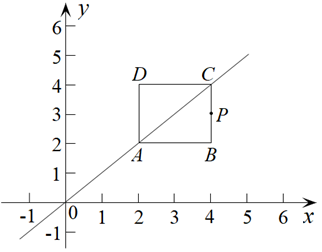 (1)、求点 的“倾斜系数”k的值;(2)、①若点 的“倾斜系数” ,请写出a和b的数量关系,并说明理由;
(1)、求点 的“倾斜系数”k的值;(2)、①若点 的“倾斜系数” ,请写出a和b的数量关系,并说明理由;②若点 的“倾斜系数” ,且 ,求OP的长;
(3)、如图,边长为2的正方形ABCD沿直线AC: 运动, 是正方形ABCD上任意一点,且点P的“倾斜系数” ,请直接写出a的取值范围.33. 综合与实践,【问题情境】:数学活动课上,老师出示了一个问题:如图1,在正方形ABCD中,E是BC的中点, ,EP与正方形的外角 的平分线交于P点.试猜想AE与EP的数量关系,并加以证明;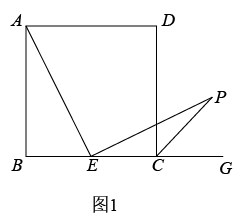
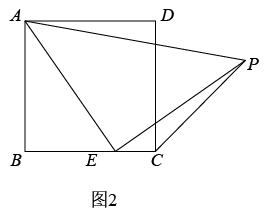
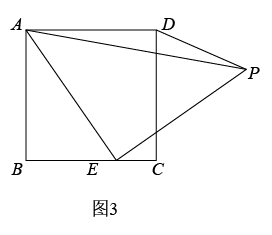 (1)、【思考尝试】同学们发现,取AB的中点F,连接EF可以解决这个问题.请在图1中补全图形,解答老师提出的问题.(2)、【实践探究】希望小组受此问题启发,逆向思考这个题目,并提出新的问题:如图2,在正方形ABCD中,E为BC边上一动点(点E,B不重合), 是等腰直角三角形, ,连接CP,可以求出 的大小,请你思考并解答这个问题.(3)、【拓展迁移】突击小组深入研究希望小组提出的这个问题,发现并提出新的探究点:如图3,在正方形ABCD中,E为BC边上一动点(点E,B不重合), 是等腰直角三角形, ,连接DP.知道正方形的边长时,可以求出 周长的最小值.当 时,请你求出 周长的最小值.34. 已知矩形ABCD,点E为直线BD上的一个动点(点E不与点B重合),连接AE,以AE为一边构造矩形AEFG(A,E,F,G按逆时针方向排列),连接DG.
(1)、【思考尝试】同学们发现,取AB的中点F,连接EF可以解决这个问题.请在图1中补全图形,解答老师提出的问题.(2)、【实践探究】希望小组受此问题启发,逆向思考这个题目,并提出新的问题:如图2,在正方形ABCD中,E为BC边上一动点(点E,B不重合), 是等腰直角三角形, ,连接CP,可以求出 的大小,请你思考并解答这个问题.(3)、【拓展迁移】突击小组深入研究希望小组提出的这个问题,发现并提出新的探究点:如图3,在正方形ABCD中,E为BC边上一动点(点E,B不重合), 是等腰直角三角形, ,连接DP.知道正方形的边长时,可以求出 周长的最小值.当 时,请你求出 周长的最小值.34. 已知矩形ABCD,点E为直线BD上的一个动点(点E不与点B重合),连接AE,以AE为一边构造矩形AEFG(A,E,F,G按逆时针方向排列),连接DG.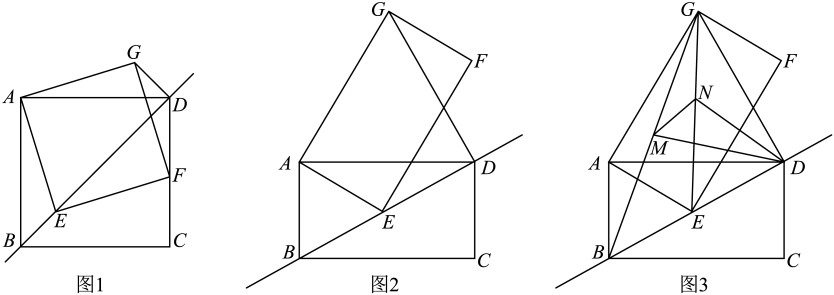 (1)、如图1,当==1时,请直接写出线段BE与线段DG的数量关系与位置关系;(2)、如图2,当==2时,请猜想线段BE与线段DG的数量关系与位置关系,并说明理由;(3)、如图3,在(2)的条件下,连接BG,EG,分别取线段BG,EG的中点M,N,连接MN,MD,ND,若AB= , ∠AEB=45°,请直接写出△MND的面积.35. 如图,在菱形ABCD中,∠BAD = 120°,AB = 6,连接BD .
(1)、如图1,当==1时,请直接写出线段BE与线段DG的数量关系与位置关系;(2)、如图2,当==2时,请猜想线段BE与线段DG的数量关系与位置关系,并说明理由;(3)、如图3,在(2)的条件下,连接BG,EG,分别取线段BG,EG的中点M,N,连接MN,MD,ND,若AB= , ∠AEB=45°,请直接写出△MND的面积.35. 如图,在菱形ABCD中,∠BAD = 120°,AB = 6,连接BD . (1)、求BD的长;(2)、点E为线段BD上一动点(不与点B,D重合), 点F在边AD上,且BE=DF,
(1)、求BD的长;(2)、点E为线段BD上一动点(不与点B,D重合), 点F在边AD上,且BE=DF,①当CE丄AB时,求四边形ABEF的面积;
②当四边形ABEF的面积取得最小值时,CE+CF的值是否也最小?如果是,求CE+CF的最小值;如果不是,请说明理由.
36. 如图,四边形ABCD为菱形,E为对角线AC上的一个动点(不与点A,C重合),连接DE并延长交射线AB于点F,连接BE. (1)、求证:;(2)、求证: .37. 平行四边形 , 若为中点,交于点 , 连接 .
(1)、求证:;(2)、求证: .37. 平行四边形 , 若为中点,交于点 , 连接 .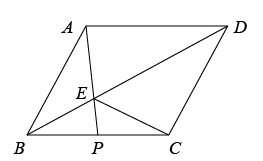 (1)、若 ,
(1)、若 ,①证明为菱形;
②若 , , 求的长.
(2)、以为圆心,为半径,为圆心,为半径作圆,两圆另一交点记为点 , 且 . 若在直线上,求的值.38.(1)、【探究发现】如图①所示,在正方形中,为边上一点,将沿翻折到处,延长交边于点.求证: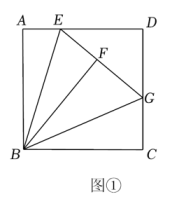 (2)、【类比迁移】如图②,在矩形中,为边上一点,且将沿翻折到处,延长交边于点延长交边于点且求的长.
(2)、【类比迁移】如图②,在矩形中,为边上一点,且将沿翻折到处,延长交边于点延长交边于点且求的长. (3)、【拓展应用】如图③,在菱形中,为边上的三等分点,AB=6,将沿翻折得到 , 直线交于点求的长.
(3)、【拓展应用】如图③,在菱形中,为边上的三等分点,AB=6,将沿翻折得到 , 直线交于点求的长.