2022年全国中考数学真题分类汇编19 四边形及多边形(1)
试卷更新日期:2022-12-29 类型:二轮复习
一、单选题
-
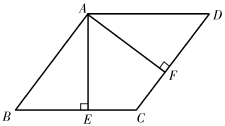
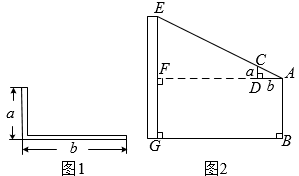
1. 西周数学家商高总结了用“矩”(如图1)测量物高的方法:把矩的两边放置成如图2的位置,从矩的一端A(人眼)望点E,使视线通过点C,记人站立的位置为点B,量出BG长,即可算得物高EG.令BG=x(m), EG=y(m),若a=30cm,b=60cm,AB=1.6m,则y关于x的函数表达式为( )
 A、 B、 C、 D、2. 如图,在菱形纸片ABCD中,E是BC边上一点,将△ABE沿直线AE翻折,使点B落在上,连接 . 已知∠C=120°,∠BAE=50°,则的度数为( )
A、 B、 C、 D、2. 如图,在菱形纸片ABCD中,E是BC边上一点,将△ABE沿直线AE翻折,使点B落在上,连接 . 已知∠C=120°,∠BAE=50°,则的度数为( )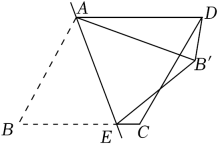 A、50° B、60° C、80° D、90°3. 如图,▱ABCD的对角线AC和BD相交于点O,下列说法正确的是( )
A、50° B、60° C、80° D、90°3. 如图,▱ABCD的对角线AC和BD相交于点O,下列说法正确的是( )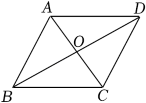 A、若OB=OD,则▱ABCD是菱形 B、若AC=BD,则▱ABCD是菱形 C、若OA=OD,则▱ABCD是菱形 D、若AC⊥BD,则▱ABCD是菱形4. 如图,正方形的对角线交于点O,点E是直线上一动点.若 , 则的最小值是( )
A、若OB=OD,则▱ABCD是菱形 B、若AC=BD,则▱ABCD是菱形 C、若OA=OD,则▱ABCD是菱形 D、若AC⊥BD,则▱ABCD是菱形4. 如图,正方形的对角线交于点O,点E是直线上一动点.若 , 则的最小值是( ) A、 B、 C、 D、5. 如图,将一张长方形纸对折,再对折,然后沿图中虚线剪下,剪下的图形展开后可得到( )
A、 B、 C、 D、5. 如图,将一张长方形纸对折,再对折,然后沿图中虚线剪下,剪下的图形展开后可得到( )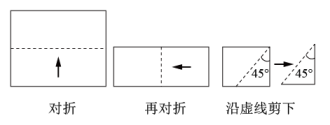 A、三角形 B、梯形 C、正方形 D、五边形6. 如图,菱形ABCD的对角线AC、BD相交于点O,过点D作DH⊥AB于点H,连接OH,OH=4,若菱形ABCD的面积为32 , 则CD的长为( )
A、三角形 B、梯形 C、正方形 D、五边形6. 如图,菱形ABCD的对角线AC、BD相交于点O,过点D作DH⊥AB于点H,连接OH,OH=4,若菱形ABCD的面积为32 , 则CD的长为( )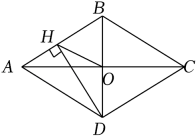 A、4 B、4 C、8 D、87. 如图,在平面直角坐标系中,矩形ABCD的顶点A在第一象限,B,D分别在y轴上,AB交x轴于点E,轴,垂足为F.若 , . 以下结论正确的个数是( )
A、4 B、4 C、8 D、87. 如图,在平面直角坐标系中,矩形ABCD的顶点A在第一象限,B,D分别在y轴上,AB交x轴于点E,轴,垂足为F.若 , . 以下结论正确的个数是( )①;②AE平分;③点C的坐标为;④;⑤矩形ABCD的面积为 .
 A、2个 B、3个 C、4个 D、5个8. 如图,在Rt△ABC中,∠A=90°,M为BC的中点,H为AB上一点,过点C作CG∥AB,交HM的延长线于点G,若AC=8,AB=6,则四边形ACGH周长的最小值是( )
A、2个 B、3个 C、4个 D、5个8. 如图,在Rt△ABC中,∠A=90°,M为BC的中点,H为AB上一点,过点C作CG∥AB,交HM的延长线于点G,若AC=8,AB=6,则四边形ACGH周长的最小值是( )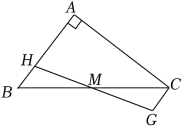 A、24 B、22 C、20 D、189. 如图,在▱ABCD中,AB=8,点E是AB上一点,AE=3,连接DE,过点C作CF∥DE,交AB的延长线于点F,则BF的长为( )
A、24 B、22 C、20 D、189. 如图,在▱ABCD中,AB=8,点E是AB上一点,AE=3,连接DE,过点C作CF∥DE,交AB的延长线于点F,则BF的长为( )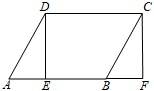 A、5 B、4 C、3 D、210. 如图,E、F、G、H分别是矩形的边AB、BC、CD、AD上的点,AH=CF,AE=CG,∠EHF=60°,∠GHF=45°.若AH=2,AD=5+ . 则四边形EFGH的周长为( )
A、5 B、4 C、3 D、210. 如图,E、F、G、H分别是矩形的边AB、BC、CD、AD上的点,AH=CF,AE=CG,∠EHF=60°,∠GHF=45°.若AH=2,AD=5+ . 则四边形EFGH的周长为( )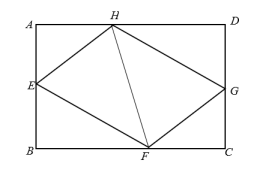 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 如图,在中, , 若 , 则的度数是.
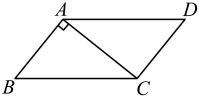 12. 如图,以的三边为边在上方分别作等边、、.且点A在内部.给出以下结论:
12. 如图,以的三边为边在上方分别作等边、、.且点A在内部.给出以下结论:①四边形是平行四边形;
②当时,四边形是矩形;
③当时,四边形是菱形;
④当 , 且时,四边形是正方形.
其中正确结论有(填上所有正确结论的序号).
 13. 如图,如果要测量池塘两端A,B的距离,可以在池塘外取一点C,连接AC,BC,点D,E分别是AC,BC的中点,测得DE的长为25米,则AB的长为 米.
13. 如图,如果要测量池塘两端A,B的距离,可以在池塘外取一点C,连接AC,BC,点D,E分别是AC,BC的中点,测得DE的长为25米,则AB的长为 米.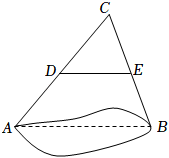 14. 小张同学家要装修,准备购买两种边长相同的正多边形瓷砖用于铺满地面.现已选定正三角形瓷砖,则选的另一种正多边形瓷砖的边数可以是 . (填一种即可)15. 如图,点O是正方形的中心, . 中,过点D,分别交于点G,M,连接 . 若 , 则的周长为 .
14. 小张同学家要装修,准备购买两种边长相同的正多边形瓷砖用于铺满地面.现已选定正三角形瓷砖,则选的另一种正多边形瓷砖的边数可以是 . (填一种即可)15. 如图,点O是正方形的中心, . 中,过点D,分别交于点G,M,连接 . 若 , 则的周长为 .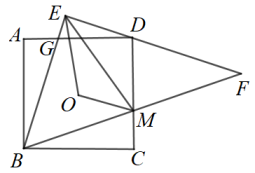 16. 已知正方形的边长为4,为上一点,连接并延长交的延长线于点 , 过点作 , 交于点 , 交于点 , 为的中点,为上一动点,分别连接 , . 若 , 则的最小值为 .
16. 已知正方形的边长为4,为上一点,连接并延长交的延长线于点 , 过点作 , 交于点 , 交于点 , 为的中点,为上一动点,分别连接 , . 若 , 则的最小值为 . 17. 如图,将边长为3的正方形ABCD沿其对角线AC平移,使A的对应点A′满足AA′=AC,则所得正方形与原正方形重叠部分的面积是 .
17. 如图,将边长为3的正方形ABCD沿其对角线AC平移,使A的对应点A′满足AA′=AC,则所得正方形与原正方形重叠部分的面积是 .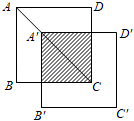 18. 如图,将矩形纸片ABCD折叠,折痕为MN,点M,N分别在边AD,BC上,点C,D的对应点分别在E,F且点F在矩形内部,MF的延长线交BC与点G,EF交边BC于点H. , , 当点H为GN三等分点时,MD的长为 .
18. 如图,将矩形纸片ABCD折叠,折痕为MN,点M,N分别在边AD,BC上,点C,D的对应点分别在E,F且点F在矩形内部,MF的延长线交BC与点G,EF交边BC于点H. , , 当点H为GN三等分点时,MD的长为 .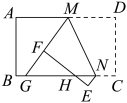 19. 矩形ABCD中, , , 点E在AB边上, . 若点P是矩形ABCD边上一点,且与点A,E构成以AE为腰的等腰三角形,则等腰三角形AEP的底边长是 .
19. 矩形ABCD中, , , 点E在AB边上, . 若点P是矩形ABCD边上一点,且与点A,E构成以AE为腰的等腰三角形,则等腰三角形AEP的底边长是 .三、作图题
-
20. 如图,是边长为的小正方形组成的方格,线段的端点在格点上.建立平面直角坐标系,使点A、B的坐标分别为和 .
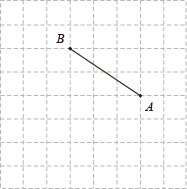
⑴画出该平面直角坐标系;
⑵画出线段关于原点成中心对称的线段;
⑶画出以点A、B、O为其中三个顶点的平行四边形.(画出一个即可)
四、解答题
-
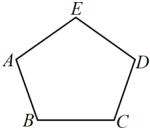
21. 同学们在探索“多边形的内角和”时,利用了“三角形的内角和”.请你在不直接运用结论“n边形的内角和为”计算的条件下,利用“一个三角形的内角和等于180°”,结合图形说明:五边形的内角和为540°.
 22. 【阅读材料】
22. 【阅读材料】老师的问题:
已知:如图, .
求作:菱形 , 使点C,D分别在上.
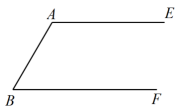
小明的作法:
(1)以A为圆心,长为半径画弧,交于点D;
(2)以B为圆心,长为半经画弧,交于点C;
(3)连接 .
四边形就是所求作的菱形,
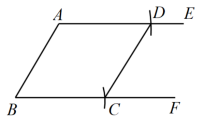
【解答问题】
请根据材料中的信息,证明四边形是菱形.
五、综合题
-
23. 如图,已知线段和线段.
 (1)、用直尺和圆规按下列要求作图.(请保留作图痕迹,并标明相应的字母,不写作法)
(1)、用直尺和圆规按下列要求作图.(请保留作图痕迹,并标明相应的字母,不写作法)①作线段的垂直平分线 , 交线段于点;
②以线段为对角线,作矩形 , 使得 , 并且点在线段的上方.
(2)、当 , 时,求(1)中所作矩形的面积.24. 在数学兴趣小组活动中,同学们对菱形的折叠问题进行了探究.如图(1),在菱形中,为锐角,为中点,连接 , 将菱形沿折叠,得到四边形 , 点的对应点为点 , 点的对应点为点.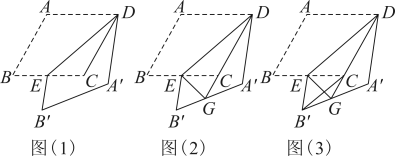 (1)、【观察发现】与的位置关系是;(2)、【思考表达】连接 , 判断与是否相等,并说明理由;(3)、如图(2),延长交于点 , 连接 , 请探究的度数,并说明理由;(4)、【综合运用】如图(3),当时,连接 , 延长交于点 , 连接 , 请写出、、之间的数量关系,并说明理由.25. 如图,在菱形ABCD中,AB=5,BD为对角线.点E是边AB延长线上的任意一点,连结DE交BC于点F,BG平分∠CBE交DE于点G.
(1)、【观察发现】与的位置关系是;(2)、【思考表达】连接 , 判断与是否相等,并说明理由;(3)、如图(2),延长交于点 , 连接 , 请探究的度数,并说明理由;(4)、【综合运用】如图(3),当时,连接 , 延长交于点 , 连接 , 请写出、、之间的数量关系,并说明理由.25. 如图,在菱形ABCD中,AB=5,BD为对角线.点E是边AB延长线上的任意一点,连结DE交BC于点F,BG平分∠CBE交DE于点G. (1)、求证:.(2)、若 .
(1)、求证:.(2)、若 .①求菱形的面积.
②求的值.
(3)、若 , 当的大小发生变化时(),在AE上找一点T,使GT为定值,说明理由并求出ET的值.26. 如图,▱ABCD中,E为BC边的中点,连接AE并延长交DC的延长线于点F,延长EC至点G,使CG=CE,连接DG、DE、FG.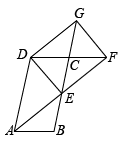 (1)、求证:△ABE≌△FCE;(2)、若AD=2AB,求证:四边形DEFG是矩形.27. 如图,在平行四边形ABCD中,点E、F在对角线BD上,且BE=DF.求证:
(1)、求证:△ABE≌△FCE;(2)、若AD=2AB,求证:四边形DEFG是矩形.27. 如图,在平行四边形ABCD中,点E、F在对角线BD上,且BE=DF.求证: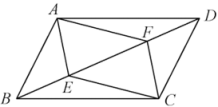 (1)、△ABE≌△CDF;(2)、四边形AECF是平行四边形.28. 如图,在矩形ABCD中,AB=BC,点F在BC边的延长线上,点P是线段BC上一点(与点B,C不重合),连接AP并延长,过点C作CG⊥AP,垂足为E.
(1)、△ABE≌△CDF;(2)、四边形AECF是平行四边形.28. 如图,在矩形ABCD中,AB=BC,点F在BC边的延长线上,点P是线段BC上一点(与点B,C不重合),连接AP并延长,过点C作CG⊥AP,垂足为E. (1)、若CG为∠DCF的平分线.请判断BP与CP的数量关系,并证明;(2)、若AB=3,△ABP≌△CEP,求BP的长.29. 已知,点、、、分别在正方形的边、、、上.
(1)、若CG为∠DCF的平分线.请判断BP与CP的数量关系,并证明;(2)、若AB=3,△ABP≌△CEP,求BP的长.29. 已知,点、、、分别在正方形的边、、、上.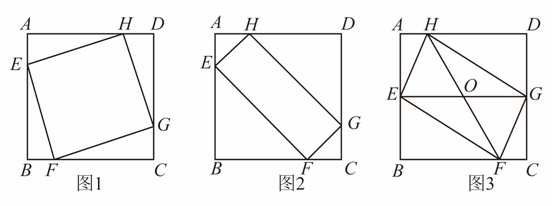 (1)、如图1,当四边形是正方形时,求证:;(2)、如图2,已知 , , 当、的大小有关系时,四边形是矩形;(3)、如图3, , 、相交于点 , , 已知正方形的边长为16,长为20,当的面积取最大值时,判断四边形是怎样的四边形?证明你的结论.30. 矩形ABCD中,=(k>1),点E是边BC的中点,连接AE,过点E作AE的垂线EF,与矩形的外角平分线CF交于点F.
(1)、如图1,当四边形是正方形时,求证:;(2)、如图2,已知 , , 当、的大小有关系时,四边形是矩形;(3)、如图3, , 、相交于点 , , 已知正方形的边长为16,长为20,当的面积取最大值时,判断四边形是怎样的四边形?证明你的结论.30. 矩形ABCD中,=(k>1),点E是边BC的中点,连接AE,过点E作AE的垂线EF,与矩形的外角平分线CF交于点F. (1)、【特例证明】如图(1),当k=2时,求证:AE=EF;
(1)、【特例证明】如图(1),当k=2时,求证:AE=EF;小明不完整的证明过程如下,请你帮他补充完整.
证明:如图,在BA上截取BH=BE,连接EH.
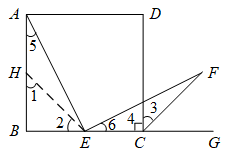
∵k=2,
∴AB=BC.
∵∠B=90°,BH=BE,
∴∠1=∠2=45°,
∴∠AHE=180°-∠1=135°.
∵CF平分∠DCG,∠DCG=90°,
∴∠3=∠DCG=45°.
∴∠ECF=∠3+∠4=135°.
∴……
(只需在答题卡对应区域写出剩余证明过程)
(2)、【类比探究】如图(2),当k≠2时,求的值(用含k的式子表示);(3)、【拓展运用】如图(3),当k=3时,P为边CD上一点,连接AP,PF,∠PAE=45°, , 求BC的长.31. 如图,四边形中,ABDC, , 于点 .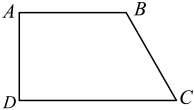 (1)、用尺规作的角平分线,交于点;(不写作法,保留作图痕迹)(2)、连接 . 求证:四边形是菱形.32. 如图,平行四边形中,边上的高 , 点E为边上的动点(不与B、C重合,过点E作直线的垂线,垂足为F,连接 .
(1)、用尺规作的角平分线,交于点;(不写作法,保留作图痕迹)(2)、连接 . 求证:四边形是菱形.32. 如图,平行四边形中,边上的高 , 点E为边上的动点(不与B、C重合,过点E作直线的垂线,垂足为F,连接 . (1)、求证:;(2)、当点E为的中点时,求的长;(3)、设的面积为y,求y与x之间的函数关系式,并求当x为何值时,y有最大值,最大值是多少?33. 如图,矩形中, , 点E在折线上运动,将绕点A顺时针旋转得到 , 旋转角等于 , 连接 .
(1)、求证:;(2)、当点E为的中点时,求的长;(3)、设的面积为y,求y与x之间的函数关系式,并求当x为何值时,y有最大值,最大值是多少?33. 如图,矩形中, , 点E在折线上运动,将绕点A顺时针旋转得到 , 旋转角等于 , 连接 . (1)、当点E在上时,作 , 垂足为M,求证;(2)、当时,求的长;(3)、连接 , 点E从点B运动到点D的过程中,试探究的最小值.34. “五一”节期间,许多露营爱好者在我市郊区露营,为遮阳和防雨会搭建一种“天幕”,其截面示意图是轴对称图形,对称轴是垂直于地面的支杆 , 用绳子拉直后系在树干上的点处,使得 , , 在一条直线上,通过调节点的高度可控制“天幕”的开合,m,m.
(1)、当点E在上时,作 , 垂足为M,求证;(2)、当时,求的长;(3)、连接 , 点E从点B运动到点D的过程中,试探究的最小值.34. “五一”节期间,许多露营爱好者在我市郊区露营,为遮阳和防雨会搭建一种“天幕”,其截面示意图是轴对称图形,对称轴是垂直于地面的支杆 , 用绳子拉直后系在树干上的点处,使得 , , 在一条直线上,通过调节点的高度可控制“天幕”的开合,m,m.
(参考数据: , , , )
(1)、天晴时打开“天幕”,若 , 求遮阳宽度(结果精确到0.1m);(2)、下雨时收拢“天幕”,从65°减少到45°,求点下降的高度(结果精确到0.1m).35. 如图,在平行四边形中,平分 , 平分 .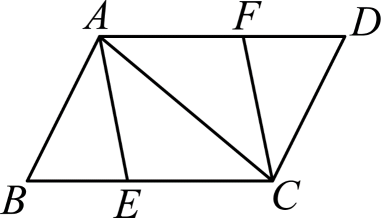 (1)、求证:;(2)、当满足什么条件时,四边形是矩形?请写出证明过程.36. 如图1,在矩形中, , , 是边上的一点,连接 , 将矩形沿折叠,顶点恰好落在边上的点处,延长交的延长线于点 .
(1)、求证:;(2)、当满足什么条件时,四边形是矩形?请写出证明过程.36. 如图1,在矩形中, , , 是边上的一点,连接 , 将矩形沿折叠,顶点恰好落在边上的点处,延长交的延长线于点 .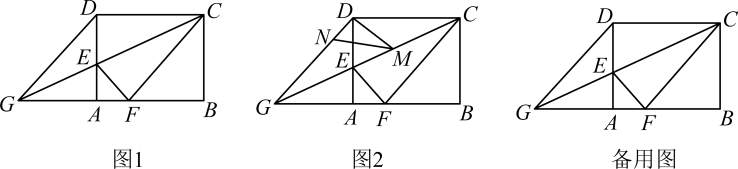 (1)、求线段的长;(2)、求证四边形为菱形;(3)、如图2, , 分别是线段 , 上的动点(与端点不重合),且 , 设 , 是否存在这样的点 , 使是直角三角形?若存在,请求出的值;若不存在,请说明理由.37. 如图,在矩形ABCD中,E为AB的中点,连接CE并延长,交DA的延长线于点F.
(1)、求线段的长;(2)、求证四边形为菱形;(3)、如图2, , 分别是线段 , 上的动点(与端点不重合),且 , 设 , 是否存在这样的点 , 使是直角三角形?若存在,请求出的值;若不存在,请说明理由.37. 如图,在矩形ABCD中,E为AB的中点,连接CE并延长,交DA的延长线于点F. (1)、求证:△AEF≌△BEC.(2)、若CD=4,∠F=30°,求CF的长.38. 如图1,在正方形ABCD中,E,F分别是BC,CD边上的点(点E不与点B,C重合),且 .
(1)、求证:△AEF≌△BEC.(2)、若CD=4,∠F=30°,求CF的长.38. 如图1,在正方形ABCD中,E,F分别是BC,CD边上的点(点E不与点B,C重合),且 . (1)、当时,求证:;(2)、猜想BE,EF,DF三条线段之间存在的数量关系,并证明你的结论;(3)、如图2,连接AC,G是CB延长线上一点, , 垂足为K,交AC于点H且 . 若 , , 请用含a,b的代数式表示EF的长.
(1)、当时,求证:;(2)、猜想BE,EF,DF三条线段之间存在的数量关系,并证明你的结论;(3)、如图2,连接AC,G是CB延长线上一点, , 垂足为K,交AC于点H且 . 若 , , 请用含a,b的代数式表示EF的长.
-