2022年全国中考数学真题分类汇编18 三角形-综合题(3)
试卷更新日期:2022-12-29 类型:二轮复习
一、作图题
-
1. 尺规作图(保留作图痕迹,不要求写出作法):
如图,已知线段m,n.求作 , 使.

二、解答题
-
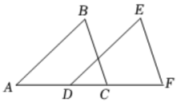
2. 已知:如图,点、、、在一条直线上,且 , , .求证:.
 3. 已知:如图, . 求证: .
3. 已知:如图, . 求证: .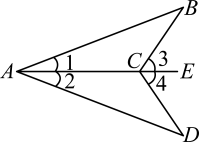 4. 如图,已知AD平分∠BAC,AB=AC.求证:△ABD≌△ACD.
4. 如图,已知AD平分∠BAC,AB=AC.求证:△ABD≌△ACD.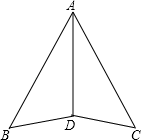 5. 如图,在Rt△ABC中,∠B=90°,CD∥AB,DE⊥AC于点E,且CE=AB.求证:△CED≌△ABC.
5. 如图,在Rt△ABC中,∠B=90°,CD∥AB,DE⊥AC于点E,且CE=AB.求证:△CED≌△ABC.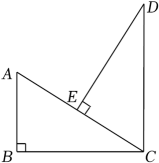 6. 如图1是小军制作的燕子风筝,燕子风筝的骨架图如图2所示, , , , ,求 的大小.
6. 如图1是小军制作的燕子风筝,燕子风筝的骨架图如图2所示, , , , ,求 的大小. 7. 如图,点D,E在△ABC的边BC上,∠B = ∠C,BD = CE,求证:△ABD≌△ACE
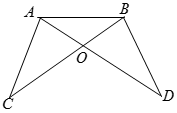
7. 如图,点D,E在△ABC的边BC上,∠B = ∠C,BD = CE,求证:△ABD≌△ACE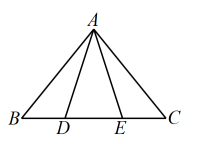 8. 如图,点D是△ABC外一点,连接BD、 AD,AD与BC交于点O.下列三个等式:①BC=AD;②∠ABC=∠BAD;③AC= BD.请从这三个等式中,任选两个作为已知条件,剩下的一个作为结论,组成一个真命题,将你选择的等式或等式的序号填在下面对应的横线上,然后对该真命题进行证明.
8. 如图,点D是△ABC外一点,连接BD、 AD,AD与BC交于点O.下列三个等式:①BC=AD;②∠ABC=∠BAD;③AC= BD.请从这三个等式中,任选两个作为已知条件,剩下的一个作为结论,组成一个真命题,将你选择的等式或等式的序号填在下面对应的横线上,然后对该真命题进行证明.已知: ▲ , ▲
求证: ▲
 9. 如图,点C在上,.求证:.
9. 如图,点C在上,.求证:. 10. 如图, , . 求证: .
10. 如图, , . 求证: .
三、综合题
-
11. 如图,在△ABC中,∠BAC=90°,AB=AC=12,点P在边AB上,D、E分别为BC、PC的中点,连接DE.过点E作BC的垂线,与BC、AC分别交于F、G两点.连接DG,交PC于点H.
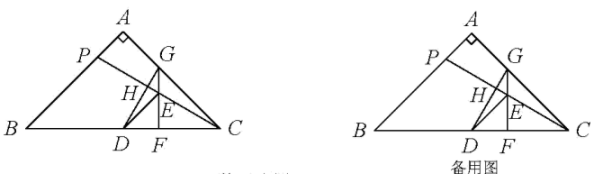 (1)、∠EDC的度数为;(2)、连接PG,求△APG 的面积的最大值;(3)、PE与DG存在怎样的位置关系与数量关系?请说明理由;(4)、求的最大值.12. 如图,在和中, , , , 且点D在线段上,连 .
(1)、∠EDC的度数为;(2)、连接PG,求△APG 的面积的最大值;(3)、PE与DG存在怎样的位置关系与数量关系?请说明理由;(4)、求的最大值.12. 如图,在和中, , , , 且点D在线段上,连 .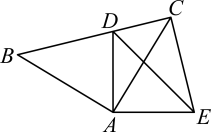 (1)、求证:;(2)、若 , 求的度数.13. 如图,在△ABC中,AB=AC,BD是△ABC的角平分线.
(1)、求证:;(2)、若 , 求的度数.13. 如图,在△ABC中,AB=AC,BD是△ABC的角平分线.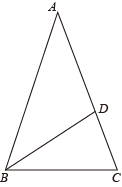 (1)、作∠ACB的角平分线,交AB于点E(尺规作图,不写作法,保留作图痕迹);(2)、求证:AD=AE.14. 综合与实践
(1)、作∠ACB的角平分线,交AB于点E(尺规作图,不写作法,保留作图痕迹);(2)、求证:AD=AE.14. 综合与实践 (1)、知识再现
(1)、知识再现
如图 , 中, , 分别以、、为边向外作的正方形的面积为、、 . 当 , 时, .(2)、问题探究如图,中, .
如图 , 分别以、、为边向外作的等腰直角三角形的面积为、、 , 则、、之间的数量关系是 .(3)、如图 , 分别以、、为边向外作的等边三角形的面积为、、 , 试猜想、、之间的数量关系,并说明理由.(4)、实践应用
如图4,将图中的绕点逆时针旋转一定角度至 , 绕点顺时针旋转一定角度至 , 、相交于点 . 求证:;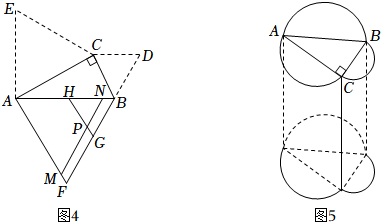 (5)、如图5,分别以图中的边、、为直径向外作半圆,再以所得图形为底面作柱体,、、为直径的半圆柱的体积分别为、、 . 若 , 柱体的高 , 直接写出的值.15. 如图,在中 , 过点C作 , 在上截取 , 上截取 , 连接 .
(5)、如图5,分别以图中的边、、为直径向外作半圆,再以所得图形为底面作柱体,、、为直径的半圆柱的体积分别为、、 . 若 , 柱体的高 , 直接写出的值.15. 如图,在中 , 过点C作 , 在上截取 , 上截取 , 连接 .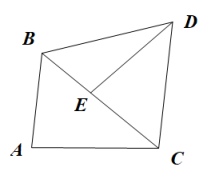 (1)、求证:;(2)、若 , 求的面积.16. 如图,在中, , , 是边上的一点,以为直角边作等腰 , 其中 , 连接 .
(1)、求证:;(2)、若 , 求的面积.16. 如图,在中, , , 是边上的一点,以为直角边作等腰 , 其中 , 连接 . (1)、求证:;(2)、若时,求的长.17. 如图,△AOB是等边三角形,过点A作y轴的垂线,垂足为C,点C的坐标为(0,).P是直线AB上在第一象限内的一动点,过点P作y轴的垂线,垂足为D,交AO于点E,连接AD,作DM⊥AD交x轴于点M,交AO于点F,连接BE,BF.
(1)、求证:;(2)、若时,求的长.17. 如图,△AOB是等边三角形,过点A作y轴的垂线,垂足为C,点C的坐标为(0,).P是直线AB上在第一象限内的一动点,过点P作y轴的垂线,垂足为D,交AO于点E,连接AD,作DM⊥AD交x轴于点M,交AO于点F,连接BE,BF. (1)、填空:若△AOD是等腰三角形,则点D的坐标为;(2)、当点P在线段AB上运动时(点P不与点A,B重合),设点M的横坐标为m.
(1)、填空:若△AOD是等腰三角形,则点D的坐标为;(2)、当点P在线段AB上运动时(点P不与点A,B重合),设点M的横坐标为m.①求m值最大时点D的坐标;
②是否存在这样的m值,使BE=BF?若存在,求出此时的m值;若不存在,请说明理由.
18. 如图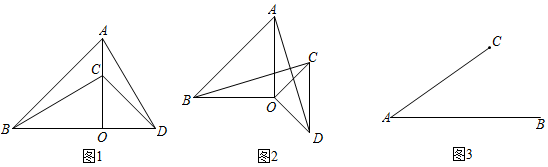 (1)、如图1,和是等腰直角三角形, , 点C在OA上,点D在线段BO延长线上,连接AD,BC.线段AD与BC的数量关系为;(2)、如图2,将图1中的绕点O顺时针旋转()第一问的结论是否仍然成立;如果成立,证明你的结论,若不成立,说明理由.(3)、如图,若 , 点C是线段AB外一动点, , 连接BC,
(1)、如图1,和是等腰直角三角形, , 点C在OA上,点D在线段BO延长线上,连接AD,BC.线段AD与BC的数量关系为;(2)、如图2,将图1中的绕点O顺时针旋转()第一问的结论是否仍然成立;如果成立,证明你的结论,若不成立,说明理由.(3)、如图,若 , 点C是线段AB外一动点, , 连接BC,①若将CB绕点C逆时针旋转90°得到CD,连接AD,则AD的最大值 ▲ ;
②若以BC为斜边作 , (B、C、D三点按顺时针排列), , 连接AD,当时,直接写出AD的值.
19. 【经典回顾】梅文鼎是我国清初著名的数学家,他在《勾股举隅》中给出多种证明勾股定理的方法图1是其中一种方法的示意图及部分辅助线.

在中, , 四边形、和分别是以的三边为一边的正方形.延长和 , 交于点 , 连接并延长交于点 , 交于点 , 延长交于点 .
(1)、证明:;(2)、证明:正方形的面积等于四边形的面积;(3)、请利用(2)中的结论证明勾股定理.(4)、【迁移拓展】如图2,四边形和分别是以的两边为一边的平行四边形,探索在下方是否存在平行四边形 , 使得该平行四边形的面积等于平行四边形、的面积之和.若存在,作出满足条件的平行四边形(保留适当的作图痕迹);若不存在,请说明理由.
20. 如图,点 , , , 在同一条直线上, , 有下列三个条件: , , .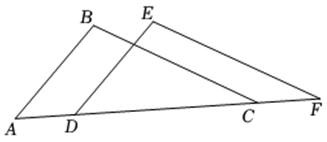 (1)、请在上述三个条件中选取一个条件,使得 ≌ .
(1)、请在上述三个条件中选取一个条件,使得 ≌ .你选取的条件为 ( 填写序号 ) ( 只需选一个条件,多选不得分 ),你判定 ≌ 的依据是 (填“ ”或“ ”或“ ”或“ ”);
(2)、利用 的结论 ≌ 求证: .21. 在△ABC中,AB=AC,∠BAC=90°,AD是△ABC的角平分线.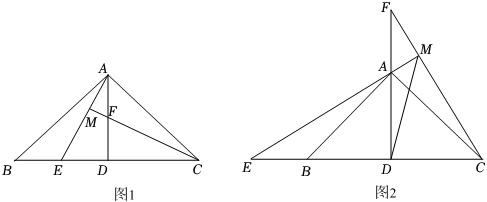 (1)、如图1,点E、F分别是线段BD、AD上的点,且DE=DF,AE与CF的延长线交于点M,则AE与CF的数量关系是 , 位置关系是;(2)、如图2,点E、F分别在DB和DA的延长线上,且DE=DF,EA的延长线交CF于点M.
(1)、如图1,点E、F分别是线段BD、AD上的点,且DE=DF,AE与CF的延长线交于点M,则AE与CF的数量关系是 , 位置关系是;(2)、如图2,点E、F分别在DB和DA的延长线上,且DE=DF,EA的延长线交CF于点M.①(1)中的结论还成立吗?如果成立,请给出证明;如果不成立,请说明理由;
②连接DM,求∠EMD的度数;
③若DM=6 , ED=12,求EM的长.
22. 如图1,在中,于点D,在DA上取点E,使 , 连接BE、CE.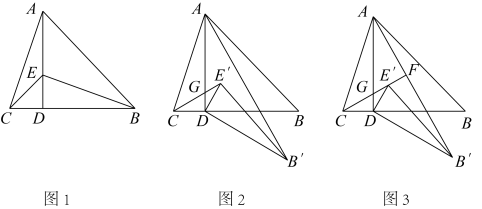 (1)、直接写出CE与AB的位置关系;(2)、如图2,将绕点D旋转,得到(点 , 分别与点B,E对应),连接 , 在旋转的过程中与的位置关系与(1)中的CE与AB的位置关系是否一致?请说明理由;(3)、如图3,当绕点D顺时针旋转30°时,射线与AD、分别交于点G、F,若 , 求的长.23. 综合与实践
(1)、直接写出CE与AB的位置关系;(2)、如图2,将绕点D旋转,得到(点 , 分别与点B,E对应),连接 , 在旋转的过程中与的位置关系与(1)中的CE与AB的位置关系是否一致?请说明理由;(3)、如图3,当绕点D顺时针旋转30°时,射线与AD、分别交于点G、F,若 , 求的长.23. 综合与实践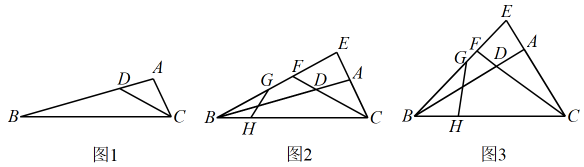 (1)、问题情境:
(1)、问题情境:数学活动课上,王老师出示了一个问题:如图1,在中,D是上一点, . 求证 .
独立思考:
请解答王老师提出的问题.
(2)、实践探究:在原有问题条件不变的情况下,王老师增加下面的条件,并提出新问题,请你解答.“如图2,延长至点E,使 , 与的延长线相交于点F,点G,H分别在上, , . 在图中找出与相等的线段,并证明.”
(3)、问题解决:数学活动小组河学时上述问题进行特殊化研究之后发现,当时,若给出中任意两边长,则图3中所有已经用字母标记的线段长均可求,该小组提出下面的问题,请你解答.“如图3,在(2)的条件下,若 , , , 求的长.”
24. 如图,在中, , , 点D在上, , 连接 , , 点P是边上一动点(点P不与点A,D,C重合),过点P作的垂线,与相交于点Q,连接 , 设 , 与重叠部分的面积为S. (1)、求的长;(2)、求S关于x的函数解析式,并直接写出自变量x的取值范围.25. 两个顶角相等的等腰三角形,如果具有公共的顶角的顶点,并把它们的底角顶点连接起来,则形成一组全等的三角形,把具有这个规律的图形称为“手拉手”图形.(1)、问题发现:
(1)、求的长;(2)、求S关于x的函数解析式,并直接写出自变量x的取值范围.25. 两个顶角相等的等腰三角形,如果具有公共的顶角的顶点,并把它们的底角顶点连接起来,则形成一组全等的三角形,把具有这个规律的图形称为“手拉手”图形.(1)、问题发现:如图1,若和是顶角相等的等腰三角形,BC,DE分别是底边.求证:;
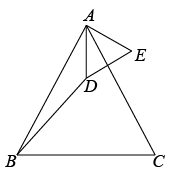
图1
(2)、解决问题:如图2,若和均为等腰直角三角形, , 点A,D,E在同一条直线上,CM为中DE边上的高,连接BE,请判断∠AEB的度数及线段CM,AE,BE之间的数量关系并说明理由.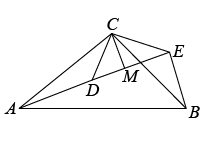
图2
26. 如图,点A,F,C,D在同一直线上,AB=DE,AF=CD,BC=EF.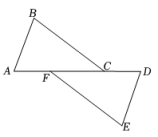 (1)、求证:∠ACB=∠DFE;(2)、连接BF,CE,直接判断四边形BFEC的形状.27. 如图所示,在等腰三角形ABC中,AB=AC,点E,F在线段BC上,点Q在线段AB上,且CF=BE,AE²=AQ·AB求证:
(1)、求证:∠ACB=∠DFE;(2)、连接BF,CE,直接判断四边形BFEC的形状.27. 如图所示,在等腰三角形ABC中,AB=AC,点E,F在线段BC上,点Q在线段AB上,且CF=BE,AE²=AQ·AB求证: (1)、∠CAE=∠BAF;(2)、CF·FQ=AF·BQ28. 在中, , 点D在线段上,连接并延长至点E,使 , 过点E作 , 交直线于点F.
(1)、∠CAE=∠BAF;(2)、CF·FQ=AF·BQ28. 在中, , 点D在线段上,连接并延长至点E,使 , 过点E作 , 交直线于点F.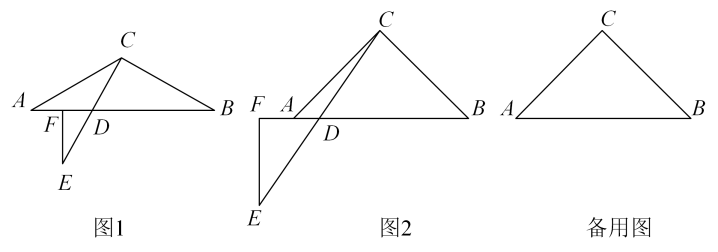 (1)、如图1,若 , 请用等式表示与的数量关系: .(2)、如图2.若 , 完成以下问题:
(1)、如图1,若 , 请用等式表示与的数量关系: .(2)、如图2.若 , 完成以下问题:①当点D,点F位于点A的异侧时,请用等式表示之间的数量关系,并说明理由;
②当点D,点F位于点A的同侧时,若 , 请直接写出的长.
29.(1)、【问题呈现】如图1,△ABC和△ADE都是等边三角形,连接BD,CE.求证:BD=CE.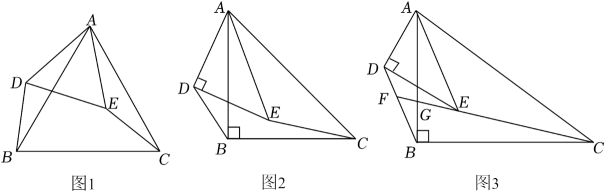 (2)、【类比探究】如图2,△ABC和△ADE都是等腰直角三角形,∠ABC=∠ADE=90°.连接BD,CE.请直接写出的值.(3)、【拓展提升】如图3,△ABC和△ADE都是直角三角形,∠ABC=∠ADE=90°,且== . 连接BD,CE.
(2)、【类比探究】如图2,△ABC和△ADE都是等腰直角三角形,∠ABC=∠ADE=90°.连接BD,CE.请直接写出的值.(3)、【拓展提升】如图3,△ABC和△ADE都是直角三角形,∠ABC=∠ADE=90°,且== . 连接BD,CE.①求的值;
②延长CE交BD于点F,交AB于点G.求sin∠BFC的值.
30. 已知:点C,D均在直线l的上方,与都是直线l的垂线段,且在的右侧, , 与相交于点O.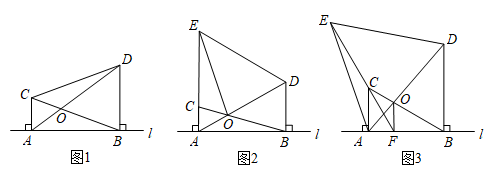 (1)、如图1,若连接 , 则的形状为 , 的值为;(2)、若将沿直线l平移,并以为一边在直线l的上方作等边.
(1)、如图1,若连接 , 则的形状为 , 的值为;(2)、若将沿直线l平移,并以为一边在直线l的上方作等边.①如图2,当与重合时,连接 , 若 , 求的长;
②如图3,当时,连接并延长交直线l于点F,连接.求证:.
31. 如图①、图②、图③均是的正方形网格,每个小正方形的边长均为1,其顶点称为格点,的顶点均在格点上.只用无刻度的直尺,在给定的网格中,按下列要求作图,保留作图痕迹.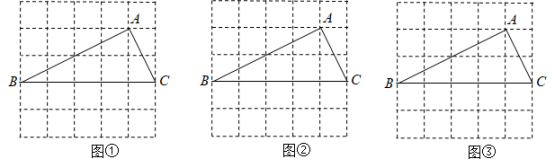 (1)、网格中的形状是;(2)、在图①中确定一点D,连结、 , 使与全等:(3)、在图②中的边上确定一点E,连结 , 使:(4)、在图③中的边上确定一点P,在边BC上确定一点Q,连结 , 使 , 且相似比为1:2.32.(1)、【情境再现】
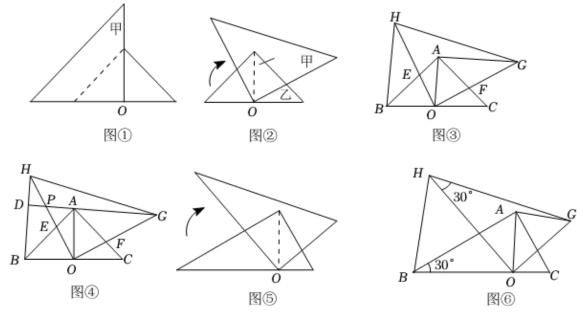
(1)、网格中的形状是;(2)、在图①中确定一点D,连结、 , 使与全等:(3)、在图②中的边上确定一点E,连结 , 使:(4)、在图③中的边上确定一点P,在边BC上确定一点Q,连结 , 使 , 且相似比为1:2.32.(1)、【情境再现】甲、乙两个含角的直角三角尺如图①放置,甲的直角顶点放在乙斜边上的高的垂足O处,将甲绕点O顺时针旋转一个锐角到图②位置.小莹用作图软件Geogebra按图②作出示意图,并连接 , 如图③所示,交于E,交于F,通过证明 , 可得 .
请你证明: .
 (2)、【迁移应用】
(2)、【迁移应用】延长分别交所在直线于点P,D,如图④,猜想并证明与的位置关系.
(3)、【拓展延伸】小亮将图②中的甲、乙换成含角的直角三角尺如图⑤,按图⑤作出示意图,并连接 , 如图⑥所示,其他条件不变,请你猜想并证明与的数量关系.
33. 如图,在中, , , 点在直线上,连接 , 将BD绕点逆时针旋转 , 得到线段 , 连接 , . (1)、求证:;(2)、当点在线段上(点不与点 , 重合)时,求的值;(3)、过点作交于点 , 若 , 请直接写出的值.34. 校园内有一块四边形的草坪造型,课外活动小组实地测量,并记录数据,根据造型画如图的四边形ABCD,其中 AB=CD=2米,AD=BC=3米,∠B=
(1)、求证:;(2)、当点在线段上(点不与点 , 重合)时,求的值;(3)、过点作交于点 , 若 , 请直接写出的值.34. 校园内有一块四边形的草坪造型,课外活动小组实地测量,并记录数据,根据造型画如图的四边形ABCD,其中 AB=CD=2米,AD=BC=3米,∠B=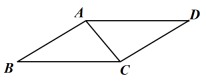 (1)、求证:△ABC≌△CDA ;(2)、求草坪造型的面积.35. 已知是的角平分线,点E,F分别在边 , 上, , , 与的面积之和为S.
(1)、求证:△ABC≌△CDA ;(2)、求草坪造型的面积.35. 已知是的角平分线,点E,F分别在边 , 上, , , 与的面积之和为S. (1)、填空:当 , , 时,
(1)、填空:当 , , 时,①如图1,若 , , 则 , ;
②如图2,若 , , 则 , ;
(2)、如图3,当时,探究S与m、n的数量关系,并说明理由:(3)、如图4,当 , , , 时,请直接写出S的大小.36. 如图,已知中, , , .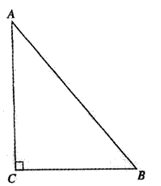 (1)、作的垂直平分线,分别交、于点、;(要求:尺规作图,不写作法,保留作图痕迹)(2)、在(1)的条件下,连接CD,求的周长.37. 在中, , D为内一点,连接 , 延长到点 , 使得
(1)、作的垂直平分线,分别交、于点、;(要求:尺规作图,不写作法,保留作图痕迹)(2)、在(1)的条件下,连接CD,求的周长.37. 在中, , D为内一点,连接 , 延长到点 , 使得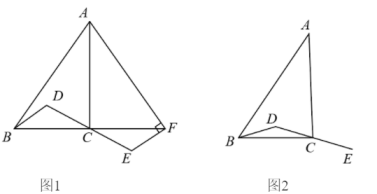 (1)、如图1,延长到点 , 使得 , 连接 , 若 , 求证:;(2)、连接 , 交的延长线于点 , 连接 , 依题意补全图2,若 , 用等式表示线段与的数量关系,并证明.38. 下面是王倩同学的作业及自主探究笔记,请认真阅读并补充完整.
(1)、如图1,延长到点 , 使得 , 连接 , 若 , 求证:;(2)、连接 , 交的延长线于点 , 连接 , 依题意补全图2,若 , 用等式表示线段与的数量关系,并证明.38. 下面是王倩同学的作业及自主探究笔记,请认真阅读并补充完整.【作业】如图①,直线 , 与的面积相等吗?为什么?
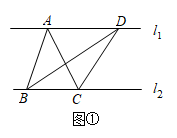
解:相等.理由如下:
设与之间的距离为 , 则 , .
∴ .
【探究】
(1)、如图②,当点在 , 之间时,设点 , 到直线的距离分别为 , , 则 .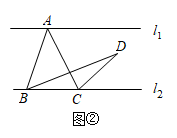
证明:∵ ▲
▲
▲
(2)、如图③,当点在 , 之间时,连接并延长交于点 , 则 .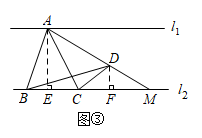
证明:过点作 , 垂足为 , 过点作 , 垂足为 , 则 ,
∴ ▲ .
∴ ▲ .
∴ .
由【探究】(1)可知 ▲ ,
∴ .
(3)、如图④,当点在下方时,连接交于点 . 若点 , , 所对应的刻度值分别为5,1.5,0,的值为 .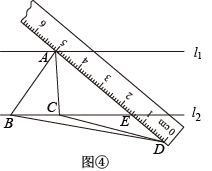
-