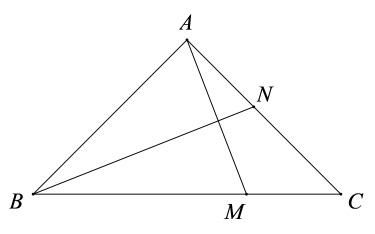2022年全国中考数学真题分类汇编18 三角形-填空题(2)
试卷更新日期:2022-12-29 类型:二轮复习
一、填空题
-
1. 如图,在中, , , , 点是边上的一点,过点作 , 交于点 , 作的平分线交于点 , 连接.若的面积是2,则的值是.
 2. 如图,依下列步骤尺规作图,并保留作图痕迹:
2. 如图,依下列步骤尺规作图,并保留作图痕迹: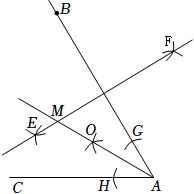
(1)分别以点A,B为圆心,大于AB的长为半径作弧,两弧相交于E,F两点,作直线EF;
(2)以点A为圆心,适当长为半径画弧,分别交AB,AC于点G,H,再分别以点G,H为圆心,大于GH的长为半径画弧,两弧在∠BAC的内部相交于点O,画射线AO,交直线EF于点M.
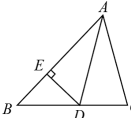
已知线段AB=6,∠BAC=60°,则点M到射线AC的距离为.3. 如图,在△ABC中,D是AC的中点,△ABC的角平分线AE交BD于点F,若BF:FD=3:1,AB+BE=3 , 则△ABC的周长为 .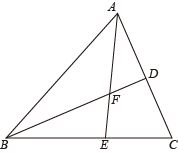 4. 如图,等边中, , 点E为高上的一动点,以为边作等边 , 连接 , , 则 , 的最小值为 .
4. 如图,等边中, , 点E为高上的一动点,以为边作等边 , 连接 , , 则 , 的最小值为 .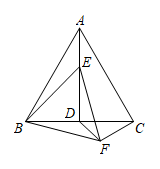 5. 如图, , 相交于点 , , 要使≌ , 添加一个条件是 . (只写一个)
5. 如图, , 相交于点 , , 要使≌ , 添加一个条件是 . (只写一个) 6. 如图,点B、F、C、E在一条直线上,AB∥ED,AC∥FD,要使△ABC≌△DEF,还需添加一个条件是 . (只需添一个)
6. 如图,点B、F、C、E在一条直线上,AB∥ED,AC∥FD,要使△ABC≌△DEF,还需添加一个条件是 . (只需添一个)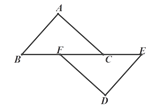 7. 如图,将绕点旋转得到 , 若 , , , 则 .
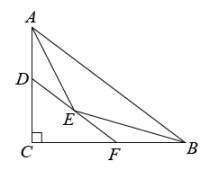
7. 如图,将绕点旋转得到 , 若 , , , 则 .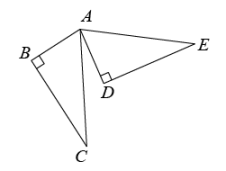 8. 如图,四边形ABCD中,∠ADC=90°,AC⊥BC,∠ABC=45°,AC与BD交于点E,若AB= , CD=2,则△ABE的面积为 .
8. 如图,四边形ABCD中,∠ADC=90°,AC⊥BC,∠ABC=45°,AC与BD交于点E,若AB= , CD=2,则△ABE的面积为 .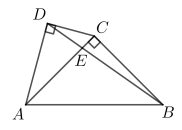 9. 如图,在平面直角坐标系xOy中,点A的坐标为(0,4),P是x轴上一动点,把线段PA绕点P顺时针旋转60°得到线段PF,连接OF,则线段OF长的最小值是 .
9. 如图,在平面直角坐标系xOy中,点A的坐标为(0,4),P是x轴上一动点,把线段PA绕点P顺时针旋转60°得到线段PF,连接OF,则线段OF长的最小值是 .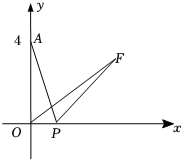 10. 《庄子▪天下篇》记载“一尺之锤,日取其半,万世不竭.”如图,直线与轴交于点 , 过点作轴的平行线交直线于点 , 过点作轴的平行线交直线于点 , 以此类推,令 , , , , 若对任意大于1的整数恒成立,则的最小值为 .
10. 《庄子▪天下篇》记载“一尺之锤,日取其半,万世不竭.”如图,直线与轴交于点 , 过点作轴的平行线交直线于点 , 过点作轴的平行线交直线于点 , 以此类推,令 , , , , 若对任意大于1的整数恒成立,则的最小值为 . 11. 如图,AB⊥BC于点B,AB⊥AD于点A,点E是CD中点,若BC=5,AD=10,BE= , 则AB的长是 .
11. 如图,AB⊥BC于点B,AB⊥AD于点A,点E是CD中点,若BC=5,AD=10,BE= , 则AB的长是 . 12. 如图,在Rt△ABC中,∠B=90°,AB=4,BC=8,分别以A,C为圆心,以大于AC的长为半径作弧,两弧相交于点P和点Q,直线PQ与AC交于点D,则AD的长为 .
12. 如图,在Rt△ABC中,∠B=90°,AB=4,BC=8,分别以A,C为圆心,以大于AC的长为半径作弧,两弧相交于点P和点Q,直线PQ与AC交于点D,则AD的长为 .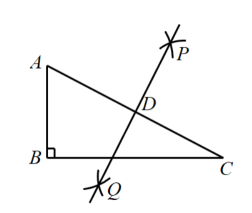 13. 如图,在△ABC中,边BC的垂直平分线DE交AB于点D,连接DC,若AB=3.7,AC=2.3,则△ADC的周长是 .
13. 如图,在△ABC中,边BC的垂直平分线DE交AB于点D,连接DC,若AB=3.7,AC=2.3,则△ADC的周长是 .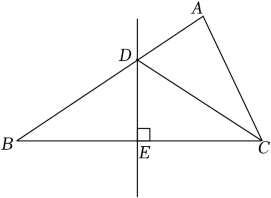 14. 如图,在△ABC中,∠A=30°,∠B=90°,D为AB中点,E在线段AC上, , 则 .
14. 如图,在△ABC中,∠A=30°,∠B=90°,D为AB中点,E在线段AC上, , 则 .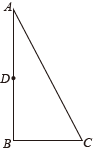 15. 如图.在 中, , .以点A为圆心,以任意长为半径作弧交AB,AC于D,E两点;分别以点D,E为圆心,以大于 长为半径作弧,在 内两弧相交于点P;作射线AP交BC于点F,过点F作 ,垂足用G.若 ,则 的周长等于cm.
15. 如图.在 中, , .以点A为圆心,以任意长为半径作弧交AB,AC于D,E两点;分别以点D,E为圆心,以大于 长为半径作弧,在 内两弧相交于点P;作射线AP交BC于点F,过点F作 ,垂足用G.若 ,则 的周长等于cm.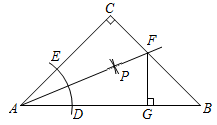 16. 如图,将绕点A逆时针旋转角得到 , 点B的对应点D恰好落在边上,若 , 则旋转角的度数是.
16. 如图,将绕点A逆时针旋转角得到 , 点B的对应点D恰好落在边上,若 , 则旋转角的度数是.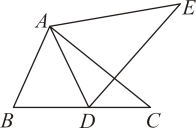 17. 小莹按照如图所示的步骤折叠A4纸,折完后,发现折痕AB′与A4纸的长边AB恰好重合,那么A4纸的长AB与宽AD的比值为 .
17. 小莹按照如图所示的步骤折叠A4纸,折完后,发现折痕AB′与A4纸的长边AB恰好重合,那么A4纸的长AB与宽AD的比值为 .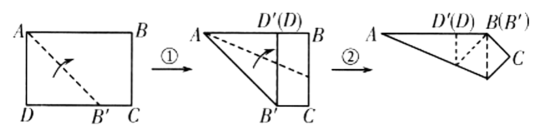 18. 如图,在中, , , , 点 , 分别在 , 上,将沿直线翻折,点的对应点恰好落在上,连接 , 若 , 则的长为 .
18. 如图,在中, , , , 点 , 分别在 , 上,将沿直线翻折,点的对应点恰好落在上,连接 , 若 , 则的长为 .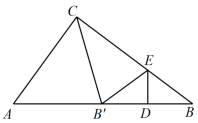 19. 如图,在中, , 点D为的中点,将绕点D逆时针旋转得到 , 当点A的对应点落在边上时,点在的延长线上,连接 , 若 , 则的面积是 .
19. 如图,在中, , 点D为的中点,将绕点D逆时针旋转得到 , 当点A的对应点落在边上时,点在的延长线上,连接 , 若 , 则的面积是 . 20. 如图,在RtABC中,∠ACB=90°,AB=13,BC=12,分别以点B和点C为圆心、大于BC的长为半径作弧,两弧相交于E,F两点,作直线EF交AB于点D,连接CD,则ACD的周长是 .
20. 如图,在RtABC中,∠ACB=90°,AB=13,BC=12,分别以点B和点C为圆心、大于BC的长为半径作弧,两弧相交于E,F两点,作直线EF交AB于点D,连接CD,则ACD的周长是 .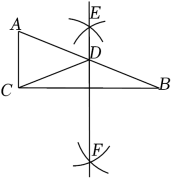 21. 等边三角形ABC中,D是边BC上的一点,BD=2CD,以AD为边作等边三角形ADE,连接CE.若CE=2,则等边三角形ABC的边长为 .22. 若(a﹣3)2+=0,则以a、b为边长的等腰三角形的周长为.23. 如图,在中, , , .在中, , , .用一条始终绷直的弹性染色线连接 , 从起始位置(点与点重合)平移至终止位置(点与点重合),且斜边始终在线段上,则的外部被染色的区域面积是.
21. 等边三角形ABC中,D是边BC上的一点,BD=2CD,以AD为边作等边三角形ADE,连接CE.若CE=2,则等边三角形ABC的边长为 .22. 若(a﹣3)2+=0,则以a、b为边长的等腰三角形的周长为.23. 如图,在中, , , .在中, , , .用一条始终绷直的弹性染色线连接 , 从起始位置(点与点重合)平移至终止位置(点与点重合),且斜边始终在线段上,则的外部被染色的区域面积是.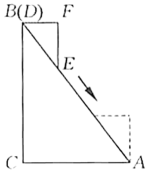 24. 如图,在中,是中线的中点.若的面积是1,则的面积是.
24. 如图,在中,是中线的中点.若的面积是1,则的面积是. 25. 如图所示的象棋盘中,各个小正方形的边长均为1.“马”从图中的位置出发,不走重复路线,按照“马走日”的规则,走两步后的落点与出发点间的最短距离为.
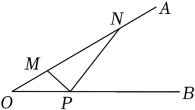
25. 如图所示的象棋盘中,各个小正方形的边长均为1.“马”从图中的位置出发,不走重复路线,按照“马走日”的规则,走两步后的落点与出发点间的最短距离为.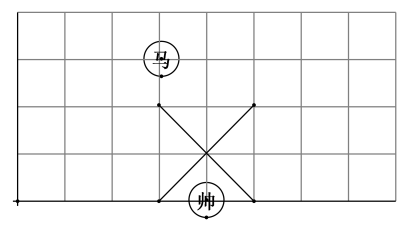 26. 如图,某雕塑MN位于河段OA上,游客P在步道上由点O出发沿OB方向行走.已知∠AOB=30°,MN=2OM=40m,当观景视角∠MPN最大时,游客P行走的距离OP是米.
26. 如图,某雕塑MN位于河段OA上,游客P在步道上由点O出发沿OB方向行走.已知∠AOB=30°,MN=2OM=40m,当观景视角∠MPN最大时,游客P行走的距离OP是米.