2022年全国中考数学真题分类汇编18 三角形-选择题(1)
试卷更新日期:2022-12-29 类型:二轮复习
一、单选题
-
1. 如图,在中, , 的平分线交于点 , 为的中点,若 , 则的长是( )
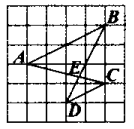
 A、8 B、6 C、5 D、42. 下列长度的三条线段能组成三角形的是( )A、3,3,6 B、3,5,10 C、4,6,9 D、4,5,93. 如图1是第七届国际数学教育大会()的会徽,在其主体图案中选择两个相邻的直角三角形,恰好能够组合得到如图2所示的四边形.若 , , , 则的值为( )
A、8 B、6 C、5 D、42. 下列长度的三条线段能组成三角形的是( )A、3,3,6 B、3,5,10 C、4,6,9 D、4,5,93. 如图1是第七届国际数学教育大会()的会徽,在其主体图案中选择两个相邻的直角三角形,恰好能够组合得到如图2所示的四边形.若 , , , 则的值为( )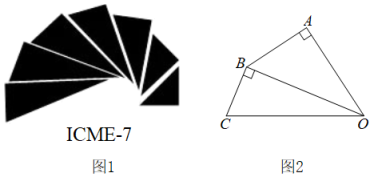 A、 B、 C、 D、14. 线段a、b、c首尾顺次相接组成三角形,若a=1,b=3,则c的长度可以是( )A、3 B、4 C、5 D、65. 如图,在△ABC中,AB=AC,∠B=36°.分别以点A,C为圆心,大于的长为半径画弧,两弧相交于点D,E,作直线DE分别交AC,BC于点F,G.以G为圆心,GC长为半径画弧,交BC于点H,连结AG,AH.则下列说法错误的是( )
A、 B、 C、 D、14. 线段a、b、c首尾顺次相接组成三角形,若a=1,b=3,则c的长度可以是( )A、3 B、4 C、5 D、65. 如图,在△ABC中,AB=AC,∠B=36°.分别以点A,C为圆心,大于的长为半径画弧,两弧相交于点D,E,作直线DE分别交AC,BC于点F,G.以G为圆心,GC长为半径画弧,交BC于点H,连结AG,AH.则下列说法错误的是( ) A、 B、 C、 D、6. 在平面直角坐标系中,直线与轴交于点 , 与轴交于点 , 将绕点逆时针旋转到如图的位置,的对应点恰好落在直线上,连接 , 则的长度为( )
A、 B、 C、 D、6. 在平面直角坐标系中,直线与轴交于点 , 与轴交于点 , 将绕点逆时针旋转到如图的位置,的对应点恰好落在直线上,连接 , 则的长度为( )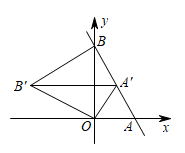 A、 B、 C、2 D、7. 如图,点、、、在网格中小正方形的顶点处,与相交于点 , 小正方形的边长为1,则的长等于( )
A、 B、 C、2 D、7. 如图,点、、、在网格中小正方形的顶点处,与相交于点 , 小正方形的边长为1,则的长等于( ) A、2 B、 C、 D、8. 如图,在中,分别以A,C为圆心,大于长为半径作弧,两弧分别相交于M,N两点,作直线 , 分别交线段 , 于点D,E,若 , 的周长为11 , 则的周长为( )
A、2 B、 C、 D、8. 如图,在中,分别以A,C为圆心,大于长为半径作弧,两弧分别相交于M,N两点,作直线 , 分别交线段 , 于点D,E,若 , 的周长为11 , 则的周长为( )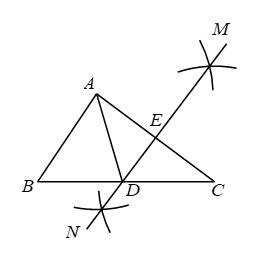 A、13 B、14 C、15 D、169. 如图所示,在中,按下列步骤作图:
A、13 B、14 C、15 D、169. 如图所示,在中,按下列步骤作图:第一步:在上分别截取 , 使;
第二步:分别以点D和点E为圆心、适当长(大于的一半)为半径作圆弧,两弧交于点F;
第三步:作射线交于点M;
第四步:过点M作于点N.
下列结论一定成立的是( )
 A、 B、 C、 D、10. 用一根小木棒与两根长分别为的小木棒组成三角形,则这根小木棒的长度可以为( )A、 B、 C、 D、11. 如图,在中, , , 是边上的中线.按下列步骤作图:①分别以点和点为圆心,大于的长为半径作弧,两弧相交于点 , ;②作直线 , 分别交 , 于点 , ;③连接 , . 则下列结论错误的是( )
A、 B、 C、 D、10. 用一根小木棒与两根长分别为的小木棒组成三角形,则这根小木棒的长度可以为( )A、 B、 C、 D、11. 如图,在中, , , 是边上的中线.按下列步骤作图:①分别以点和点为圆心,大于的长为半径作弧,两弧相交于点 , ;②作直线 , 分别交 , 于点 , ;③连接 , . 则下列结论错误的是( ) A、 B、 C、 D、12. 如图,在中, , , 是边的中点,是边上一点,若平分的周长,则的长为( )
A、 B、 C、 D、12. 如图,在中, , , 是边的中点,是边上一点,若平分的周长,则的长为( )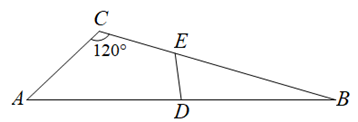 A、 B、 C、 D、13. 下列关于等边三角形的描述不正确的是( )A、是轴对称图形 B、对称轴的交点是其重心 C、是中心对称图形 D、绕重心顺时针旋转120°能与自身重合14. 如图,已知△ABC中,∠CAB=20°,∠ABC=30°,将△ABC绕A点逆时针旋转50°得到△AB′C′,以下结论:①BC=B′C′,②AC∥C′B′,③C′B′⊥BB′,④∠ABB′=∠ACC′,正确的有( )
A、 B、 C、 D、13. 下列关于等边三角形的描述不正确的是( )A、是轴对称图形 B、对称轴的交点是其重心 C、是中心对称图形 D、绕重心顺时针旋转120°能与自身重合14. 如图,已知△ABC中,∠CAB=20°,∠ABC=30°,将△ABC绕A点逆时针旋转50°得到△AB′C′,以下结论:①BC=B′C′,②AC∥C′B′,③C′B′⊥BB′,④∠ABB′=∠ACC′,正确的有( )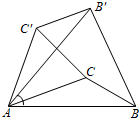 A、①②③ B、①②④ C、①③④ D、②③④15. 如图,在△ABC中,BD平分∠ABC,以点A为圆心,以任意长为半径画弧交射线AB,AC于两点,分别以这两点为圆心,以适当的定长为半径画弧,两弧交于点E,作射线AE,交BD于点I,连接CI,以下说法错误的是( )
A、①②③ B、①②④ C、①③④ D、②③④15. 如图,在△ABC中,BD平分∠ABC,以点A为圆心,以任意长为半径画弧交射线AB,AC于两点,分别以这两点为圆心,以适当的定长为半径画弧,两弧交于点E,作射线AE,交BD于点I,连接CI,以下说法错误的是( )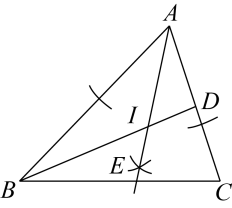 A、I到AB,AC边的距离相等 B、CI平分∠ACB C、I是△ABC的内心 D、I到A,B,C三点的距离相等16. 在如图所示的纸片中, , D是斜边AB的中点,把纸片沿着CD折叠,点B到点E的位置,连接AE.若 , , 则等于( )
A、I到AB,AC边的距离相等 B、CI平分∠ACB C、I是△ABC的内心 D、I到A,B,C三点的距离相等16. 在如图所示的纸片中, , D是斜边AB的中点,把纸片沿着CD折叠,点B到点E的位置,连接AE.若 , , 则等于( )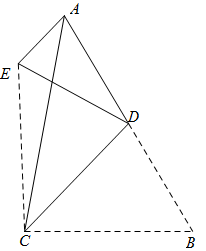 A、 B、 C、 D、17. 如图,三角形纸片ABC中,∠BAC=90°,AB=2,AC=3.沿过点A的直线将纸片折叠,使点B落在边BC上的点D处;再折叠纸片,使点C与点D重合,若折痕与AC的交点为E,则AE的长是( )
A、 B、 C、 D、17. 如图,三角形纸片ABC中,∠BAC=90°,AB=2,AC=3.沿过点A的直线将纸片折叠,使点B落在边BC上的点D处;再折叠纸片,使点C与点D重合,若折痕与AC的交点为E,则AE的长是( ) A、 B、 C、 D、18. 如图,在中, , 点D、E分别是直角边AC、BC的中点,连接DE,则度数是( )
A、 B、 C、 D、18. 如图,在中, , 点D、E分别是直角边AC、BC的中点,连接DE,则度数是( )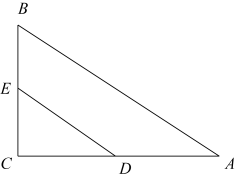 A、70° B、60° C、30° D、20°19. 若长度是4,6,a的三条线段能组成一个三角形,则a的值可以是( )A、2 B、5 C、10 D、1120. 如图,∠MON=60°,以点O为圆心,适当长为半径画弧,交OM于点A,交ON于点B;分别以点A,B为圆心,大于AB的长为半径画弧,两弧在∠MON的内部相交于点P,画射线OP;连接AB,AP,BP,过点P作PE⊥OM于点E,PF⊥ON于点F.则以下结论错误的是( )
A、70° B、60° C、30° D、20°19. 若长度是4,6,a的三条线段能组成一个三角形,则a的值可以是( )A、2 B、5 C、10 D、1120. 如图,∠MON=60°,以点O为圆心,适当长为半径画弧,交OM于点A,交ON于点B;分别以点A,B为圆心,大于AB的长为半径画弧,两弧在∠MON的内部相交于点P,画射线OP;连接AB,AP,BP,过点P作PE⊥OM于点E,PF⊥ON于点F.则以下结论错误的是( ) A、△AOB是等边三角形 B、PE=PF C、△PAE≌△PBF D、四边形OAPB是菱形21. 如图,∠AOE=15°,OE平分∠AOB,DE∥OB交OA于点D,EC⊥OB,垂足为C.若EC=2,则OD的长为( )
A、△AOB是等边三角形 B、PE=PF C、△PAE≌△PBF D、四边形OAPB是菱形21. 如图,∠AOE=15°,OE平分∠AOB,DE∥OB交OA于点D,EC⊥OB,垂足为C.若EC=2,则OD的长为( ) A、2 B、2 C、4 D、4+222. 如图,在中, , D是AB的中点,延长CB至点E,使 , 连接DE,F为DE中点,连接BF.若 , , 则BF的长为( )
A、2 B、2 C、4 D、4+222. 如图,在中, , D是AB的中点,延长CB至点E,使 , 连接DE,F为DE中点,连接BF.若 , , 则BF的长为( )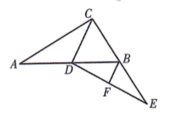 A、5 B、4 C、6 D、823. 如图,在中, , 分别以点A和点C为圆心,大于的长为半径作弧,两弧相交于M,N两点,作直线 , 直线与相交于点D,连接 , 若 , 则的长是( )
A、5 B、4 C、6 D、823. 如图,在中, , 分别以点A和点C为圆心,大于的长为半径作弧,两弧相交于M,N两点,作直线 , 直线与相交于点D,连接 , 若 , 则的长是( )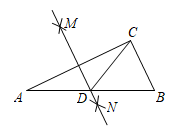 A、6 B、3 C、1.5 D、124. 如图,在中,根据尺规作图痕迹,下列说法不一定正确的是( )
A、6 B、3 C、1.5 D、124. 如图,在中,根据尺规作图痕迹,下列说法不一定正确的是( ) A、 B、 C、 D、25. 如图,在网格正方形中,每个小正方形的边长为1,顶点为格点,若的顶点均是格点,则的值是( )
A、 B、 C、 D、25. 如图,在网格正方形中,每个小正方形的边长为1,顶点为格点,若的顶点均是格点,则的值是( ) A、 B、 C、 D、26. 如图,中,若 , , 根据图中尺规作图的痕迹推断,以下结论错误的是( )
A、 B、 C、 D、26. 如图,中,若 , , 根据图中尺规作图的痕迹推断,以下结论错误的是( ) A、 B、 C、 D、27. 如图,在中, , , 延长到点 , 使 , 连接 , 则的度数( )
A、 B、 C、 D、27. 如图,在中, , , 延长到点 , 使 , 连接 , 则的度数( )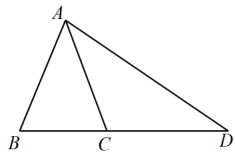 A、 B、 C、 D、28. 如图,已知 , 点为边上一点, , 点为线段的中点,以点为圆心,线段长为半径作弧,交于点 , 连接 , 则的长是( )
A、 B、 C、 D、28. 如图,已知 , 点为边上一点, , 点为线段的中点,以点为圆心,线段长为半径作弧,交于点 , 连接 , 则的长是( )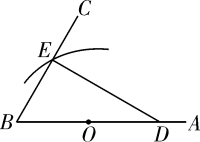 A、5 B、 C、 D、29. 活动探究:我们知道,已知两边和其中一边的对角对应相等的两个三角形不一定全等,如已知△ABC中,∠A=30°, AC=3,∠A所对的边为 , 满足已知条件的三角形有两个(我们发现其中如图的△ABC是一个直角三角形),则满足已知条件的三角形的第三边长为( )
A、5 B、 C、 D、29. 活动探究:我们知道,已知两边和其中一边的对角对应相等的两个三角形不一定全等,如已知△ABC中,∠A=30°, AC=3,∠A所对的边为 , 满足已知条件的三角形有两个(我们发现其中如图的△ABC是一个直角三角形),则满足已知条件的三角形的第三边长为( ) A、 B、 C、或 D、或30. 如图,是求作线段AB中点的作图痕迹,则下列结论不一定成立的是( )
A、 B、 C、或 D、或30. 如图,是求作线段AB中点的作图痕迹,则下列结论不一定成立的是( ) A、∠B=45° B、AE=EB C、AC=BC D、AB⊥CD
A、∠B=45° B、AE=EB C、AC=BC D、AB⊥CD