2022年全国中考数学真题分类汇编15 二次函数实际应用-几何问题
试卷更新日期:2022-12-29 类型:二轮复习
一、综合题
-
1. 如图,在平面直角坐标系中,经过点的直线AB与y轴交于点 . 经过原点O的抛物线交直线AB于点A,C,抛物线的顶点为D.
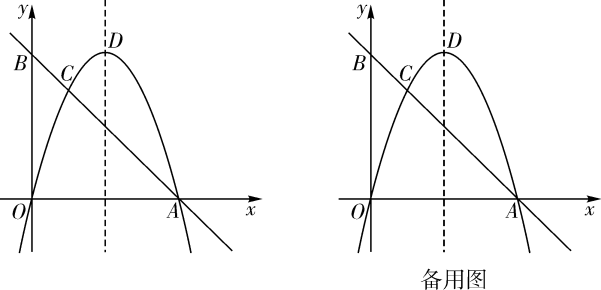 (1)、求抛物线的表达式;(2)、M是线段AB上一点,N是抛物线上一点,当轴且时,求点M的坐标;(3)、P是抛物线上一动点,Q是平面直角坐标系内一点.是否存在以点A,C,P,Q为顶点的四边形是矩形?若存在,直接写出点Q的坐标;若不存在,请说明理由.2. 如图,抛物线y=ax2+bx+c交x轴于A(-1,0),B两点,交y轴于点C(0,3),顶点D的横坐标为1.
(1)、求抛物线的表达式;(2)、M是线段AB上一点,N是抛物线上一点,当轴且时,求点M的坐标;(3)、P是抛物线上一动点,Q是平面直角坐标系内一点.是否存在以点A,C,P,Q为顶点的四边形是矩形?若存在,直接写出点Q的坐标;若不存在,请说明理由.2. 如图,抛物线y=ax2+bx+c交x轴于A(-1,0),B两点,交y轴于点C(0,3),顶点D的横坐标为1.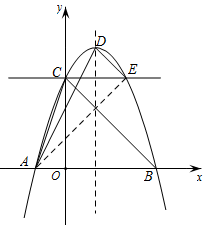 (1)、求抛物线的解析式;(2)、在y轴的负半轴上是否存在点P使∠APB+∠ACB=180°.若存在,求出点P的坐标,若不存在,请说明理由;(3)、过点C作直线l与y轴垂直,与抛物线的另一个交点为E,连接AD,AE,DE,在直线l下方的抛物线上是否存在一点M,过点M作MF⊥l,垂足为F,使以M,F,E三点为顶点的三角形与ΔADE相似?若存在,请求出M点的坐标,若不存在,请说明理由.3. 如图,在平面直角坐标系xOy中,抛物线E:y=﹣(x﹣m)2+2m2(m<0)的顶点P在抛物线F:y=ax2上,直线x=t与抛物线E,F分别交于点A,B.
(1)、求抛物线的解析式;(2)、在y轴的负半轴上是否存在点P使∠APB+∠ACB=180°.若存在,求出点P的坐标,若不存在,请说明理由;(3)、过点C作直线l与y轴垂直,与抛物线的另一个交点为E,连接AD,AE,DE,在直线l下方的抛物线上是否存在一点M,过点M作MF⊥l,垂足为F,使以M,F,E三点为顶点的三角形与ΔADE相似?若存在,请求出M点的坐标,若不存在,请说明理由.3. 如图,在平面直角坐标系xOy中,抛物线E:y=﹣(x﹣m)2+2m2(m<0)的顶点P在抛物线F:y=ax2上,直线x=t与抛物线E,F分别交于点A,B.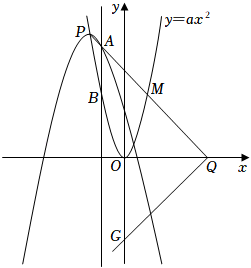 (1)、求a的值;(2)、将A,B的纵坐标分别记为yA,yB,设s=yA﹣yB,若s的最大值为4,则m的值是多少?(3)、Q是x轴的正半轴上一点,且PQ的中点M恰好在抛物线F上.试探究:此时无论m为何负值,在y轴的负半轴上是否存在定点G,使∠PQG总为直角?若存在,请求出点G的坐标;若不存在,请说明理由.4. 定义:由两条与x轴有着相同的交点,并且开口方向相同的抛物线所围成的封闭曲线称为“月牙线”,如图①,抛物线C1:y=x2+2x﹣3与抛物线C2:y=ax2+2ax+c组成一个开口向上的“月牙线”,抛物线C1和抛物线C2与x轴有着相同的交点A(﹣3,0)、B(点B在点A右侧),与y轴的交点分别为G、H(0,﹣1).
(1)、求a的值;(2)、将A,B的纵坐标分别记为yA,yB,设s=yA﹣yB,若s的最大值为4,则m的值是多少?(3)、Q是x轴的正半轴上一点,且PQ的中点M恰好在抛物线F上.试探究:此时无论m为何负值,在y轴的负半轴上是否存在定点G,使∠PQG总为直角?若存在,请求出点G的坐标;若不存在,请说明理由.4. 定义:由两条与x轴有着相同的交点,并且开口方向相同的抛物线所围成的封闭曲线称为“月牙线”,如图①,抛物线C1:y=x2+2x﹣3与抛物线C2:y=ax2+2ax+c组成一个开口向上的“月牙线”,抛物线C1和抛物线C2与x轴有着相同的交点A(﹣3,0)、B(点B在点A右侧),与y轴的交点分别为G、H(0,﹣1).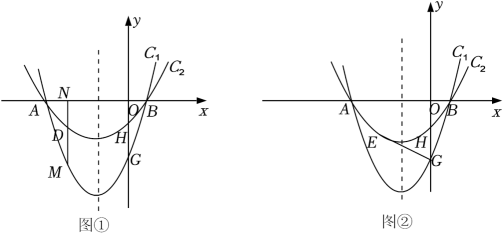 (1)、求抛物线C2的解析式和点G的坐标.(2)、点M是x轴下方抛物线C1上的点,过点M作MN⊥x轴于点N,交抛物线C2于点D,求线段MN与线段DM的长度的比值.(3)、如图②,点E是点H关于抛物线对称轴的对称点,连接EG,在x轴上是否存在点F,使得△EFG是以EG为腰的等腰三角形?若存在,请求出点F的坐标;若不存在,请说明理由.5. 如图,平行四边形ABCD中,DB= , AB=4,AD=2,动点E,F同时从A点出发,点E沿着A→D→B的路线匀速运动,点F沿着A→B→D的路线匀速运动,当点E,F相遇时停止运动.
(1)、求抛物线C2的解析式和点G的坐标.(2)、点M是x轴下方抛物线C1上的点,过点M作MN⊥x轴于点N,交抛物线C2于点D,求线段MN与线段DM的长度的比值.(3)、如图②,点E是点H关于抛物线对称轴的对称点,连接EG,在x轴上是否存在点F,使得△EFG是以EG为腰的等腰三角形?若存在,请求出点F的坐标;若不存在,请说明理由.5. 如图,平行四边形ABCD中,DB= , AB=4,AD=2,动点E,F同时从A点出发,点E沿着A→D→B的路线匀速运动,点F沿着A→B→D的路线匀速运动,当点E,F相遇时停止运动. (1)、如图1,设点E的速度为1个单位每秒,点F的速度为4个单位每秒,当运动时间为秒时,设CE与DF交于点P,求线段EP与CP长度的比值;(2)、如图2,设点E的速度为1个单位每秒,点F的速度为个单位每秒,运动时间为x秒,ΔAEF的面积为y,求y关于x的函数解析式,并指出当x为何值时,y的值最大,最大值为多少?(3)、如图3,H在线段AB上且AH=HB,M为DF的中点,当点E、F分别在线段AD、AB上运动时,探究点E、F在什么位置能使EM=HM.并说明理由.6. 已知抛物线与x轴有公共点.
(1)、如图1,设点E的速度为1个单位每秒,点F的速度为4个单位每秒,当运动时间为秒时,设CE与DF交于点P,求线段EP与CP长度的比值;(2)、如图2,设点E的速度为1个单位每秒,点F的速度为个单位每秒,运动时间为x秒,ΔAEF的面积为y,求y关于x的函数解析式,并指出当x为何值时,y的值最大,最大值为多少?(3)、如图3,H在线段AB上且AH=HB,M为DF的中点,当点E、F分别在线段AD、AB上运动时,探究点E、F在什么位置能使EM=HM.并说明理由.6. 已知抛物线与x轴有公共点.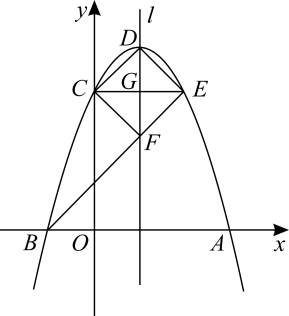 (1)、当y随x的增大而增大时,求自变量x的取值范围;(2)、将抛物线先向上平移4个单位长度,再向右平移n个单位长度得到抛物线(如图所示),抛物线与x轴交于点A,B(点A在点B的右侧),与y轴交于点C.当OC=OA时,求n的值;(3)、D为抛物线的顶点,过点C作抛物线的对称轴l的垂线,垂足为G,交抛物线于点E,连接BE交l于点F.求证:四边形CDEF是正方形.7. 在平面直角坐标系xOy中,已知抛物线y=-x2+2mx+3m,点A(3,0).
(1)、当y随x的增大而增大时,求自变量x的取值范围;(2)、将抛物线先向上平移4个单位长度,再向右平移n个单位长度得到抛物线(如图所示),抛物线与x轴交于点A,B(点A在点B的右侧),与y轴交于点C.当OC=OA时,求n的值;(3)、D为抛物线的顶点,过点C作抛物线的对称轴l的垂线,垂足为G,交抛物线于点E,连接BE交l于点F.求证:四边形CDEF是正方形.7. 在平面直角坐标系xOy中,已知抛物线y=-x2+2mx+3m,点A(3,0).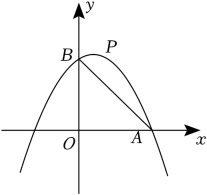 (1)、当抛物线过点A时,求抛物线的解析式;(2)、证明:无论m为何值,抛物线必过定点D,并求出点D的坐标;(3)、在(1)的条件下,抛物线与y轴交于点B,点P是抛物线上位于第一象限的点,连接AB,PD交于点M,PD与y轴交于点N.设S=S△PAM-S△BMN,问是否存在这样的点P,使得S有最大值?若存在,请求出点P的坐标,并求出S的最大值;若不存在,请说明理由.8. 如图1,抛物线y=ax2+x+c(a≠0)与x轴交于A(﹣2,0),B(6,0)两点,与y轴交于点C,点P是第一象限内抛物线上的一个动点,过点P作PD⊥x轴,垂足为D,PD交直线BC于点E,设点P的横坐标为m.
(1)、当抛物线过点A时,求抛物线的解析式;(2)、证明:无论m为何值,抛物线必过定点D,并求出点D的坐标;(3)、在(1)的条件下,抛物线与y轴交于点B,点P是抛物线上位于第一象限的点,连接AB,PD交于点M,PD与y轴交于点N.设S=S△PAM-S△BMN,问是否存在这样的点P,使得S有最大值?若存在,请求出点P的坐标,并求出S的最大值;若不存在,请说明理由.8. 如图1,抛物线y=ax2+x+c(a≠0)与x轴交于A(﹣2,0),B(6,0)两点,与y轴交于点C,点P是第一象限内抛物线上的一个动点,过点P作PD⊥x轴,垂足为D,PD交直线BC于点E,设点P的横坐标为m.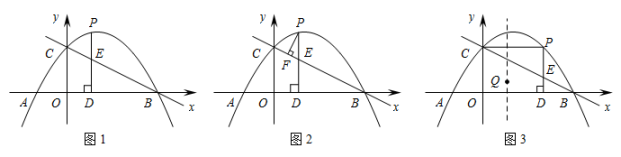 (1)、求抛物线的表达式;(2)、设线段PE的长度为h,请用含有m的代数式表示h;(3)、如图2,过点P作PF⊥CE,垂足为F,当CF=EF时,请求出m的值;(4)、如图3,连接CP,当四边形OCPD是矩形时,在抛物线的对称轴上存在点Q,使原点O关于直线CQ的对称点O′恰好落在该矩形对角线所在的直线上,请直接写出满足条件的点Q的坐标.9. 如图,在平面直角坐标系中,抛物线y=ax2+bx+2经过A( , 0),B(3,)两点,与y轴交于点C.
(1)、求抛物线的表达式;(2)、设线段PE的长度为h,请用含有m的代数式表示h;(3)、如图2,过点P作PF⊥CE,垂足为F,当CF=EF时,请求出m的值;(4)、如图3,连接CP,当四边形OCPD是矩形时,在抛物线的对称轴上存在点Q,使原点O关于直线CQ的对称点O′恰好落在该矩形对角线所在的直线上,请直接写出满足条件的点Q的坐标.9. 如图,在平面直角坐标系中,抛物线y=ax2+bx+2经过A( , 0),B(3,)两点,与y轴交于点C.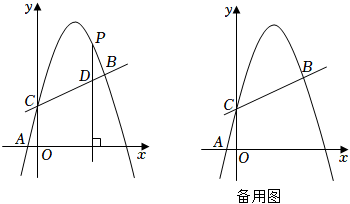 (1)、求抛物线的解析式;(2)、点P在抛物线上,过P作PD⊥x轴,交直线BC于点D,若以P、D、O、C为顶点的四边形是平行四边形,求点P的横坐标;(3)、抛物线上是否存在点Q,使∠QCB=45°?若存在,请直接写出点Q的坐标;若不存在,请说明理由.10. 如图①,已知抛物线L:y=x2+bx+c的图象经过点A(0,3),B(1,0),过点A作ACx轴交抛物线于点C,∠AOB的平分线交线段AC于点E,点P是抛物线上的一个动点.
(1)、求抛物线的解析式;(2)、点P在抛物线上,过P作PD⊥x轴,交直线BC于点D,若以P、D、O、C为顶点的四边形是平行四边形,求点P的横坐标;(3)、抛物线上是否存在点Q,使∠QCB=45°?若存在,请直接写出点Q的坐标;若不存在,请说明理由.10. 如图①,已知抛物线L:y=x2+bx+c的图象经过点A(0,3),B(1,0),过点A作ACx轴交抛物线于点C,∠AOB的平分线交线段AC于点E,点P是抛物线上的一个动点.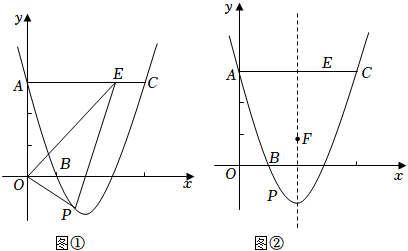 (1)、求抛物线的关系式;(2)、若动点P在直线OE下方的抛物线上,连结PE、PO,当△OPE面积最大时,求出P点坐标;(3)、将抛物线L向上平移h个单位长度,使平移后所得抛物线的顶点落在△OAE内(包括△OAE的边界),求h的取值范围;(4)、如图②,F是抛物线的对称轴l上的一点,在抛物线上是否存在点P,使△POF成为以点P为直角顶点的等腰直角三角形?若存在,直接写出所有符合条件的点P的坐标;若不存在,请说明理由.11. 如图,抛物线与x轴交于两点,与y轴交于点 , 连接AC、BC.
(1)、求抛物线的关系式;(2)、若动点P在直线OE下方的抛物线上,连结PE、PO,当△OPE面积最大时,求出P点坐标;(3)、将抛物线L向上平移h个单位长度,使平移后所得抛物线的顶点落在△OAE内(包括△OAE的边界),求h的取值范围;(4)、如图②,F是抛物线的对称轴l上的一点,在抛物线上是否存在点P,使△POF成为以点P为直角顶点的等腰直角三角形?若存在,直接写出所有符合条件的点P的坐标;若不存在,请说明理由.11. 如图,抛物线与x轴交于两点,与y轴交于点 , 连接AC、BC.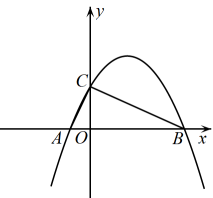
 (1)、求抛物线的表达式;(2)、将沿AC所在直线折叠,得到 , 点B的对应点为D,直接写出点D的坐标.并求出四边形OADC的面积;(3)、点P是抛物线上的一动点,当时,求点P的坐标.12. 抛物线与x轴交于 , 两点,与y轴交于点C,直线y=kx-6经过点B.点P在抛物线上,设点P的横坐标为m.
(1)、求抛物线的表达式;(2)、将沿AC所在直线折叠,得到 , 点B的对应点为D,直接写出点D的坐标.并求出四边形OADC的面积;(3)、点P是抛物线上的一动点,当时,求点P的坐标.12. 抛物线与x轴交于 , 两点,与y轴交于点C,直线y=kx-6经过点B.点P在抛物线上,设点P的横坐标为m.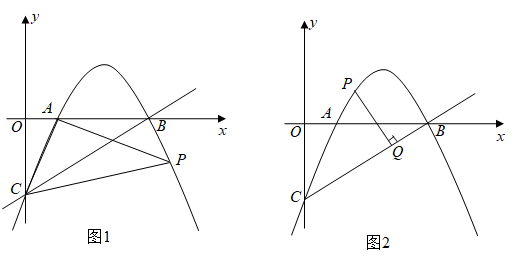 (1)、求抛物线的表达式和t,k的值;(2)、如图1,连接AC,AP,PC,若△APC是以CP为斜边的直角三角形,求点P的坐标;(3)、如图2,若点P在直线BC上方的抛物线上,过点P作PQ⊥BC,垂足为Q,求的最大值.13. 如图1,抛物线与x轴交于 , 两点,与y轴交于点C.
(1)、求抛物线的表达式和t,k的值;(2)、如图1,连接AC,AP,PC,若△APC是以CP为斜边的直角三角形,求点P的坐标;(3)、如图2,若点P在直线BC上方的抛物线上,过点P作PQ⊥BC,垂足为Q,求的最大值.13. 如图1,抛物线与x轴交于 , 两点,与y轴交于点C.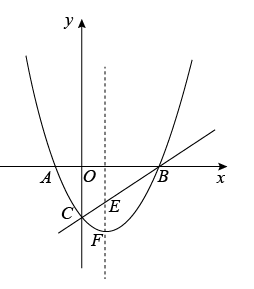
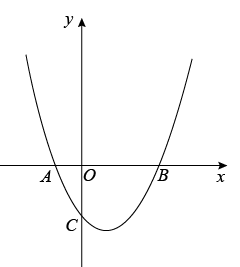
图1 图2
(1)、求该抛物线的解析式;(2)、若点E是抛物线的对称轴与直线BC的交点,点F是抛物线的顶点,求EF的长;(3)、设点P是(1)中抛物线上的一个动点,是否存在满足的点P?如果存在,请求出点P的坐标;若不存在,请说明理由.(请在图2中探讨)14. 在平面直角坐标系中,抛物线与x轴相交于点A,B(点A在点B的左侧),与y轴相交于点C,连接 .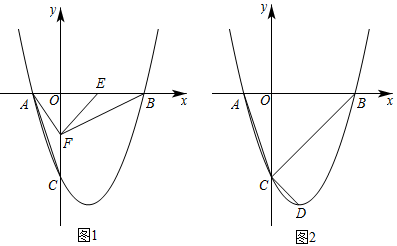 (1)、求点B,点C的坐标;(2)、如图1,点在线段上(点E不与点B重合),点F在y轴负半轴上, , 连接 , 设的面积为 , 的面积为 , , 当S取最大值时,求m的值;(3)、如图2,抛物线的顶点为D,连接 , 点P在第一象限的抛物线上,与相交于点Q,是否存在点P,使 , 若存在,请求出点P的坐标;若不存在,请说明理由.15. 如图,抛物线与轴交于 , 两点,与轴交于点,直线方程为 .
(1)、求点B,点C的坐标;(2)、如图1,点在线段上(点E不与点B重合),点F在y轴负半轴上, , 连接 , 设的面积为 , 的面积为 , , 当S取最大值时,求m的值;(3)、如图2,抛物线的顶点为D,连接 , 点P在第一象限的抛物线上,与相交于点Q,是否存在点P,使 , 若存在,请求出点P的坐标;若不存在,请说明理由.15. 如图,抛物线与轴交于 , 两点,与轴交于点,直线方程为 .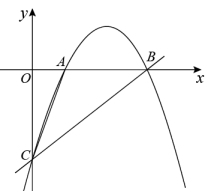 (1)、求抛物线的解析式;(2)、点为抛物线上一点,若 , 请直接写出点的坐标;(3)、点是抛物线上一点,若 , 求点的坐标.16. 如图,抛物线与x轴交于两点(A在B的左侧),与y轴交于点 , 点P在抛物线上,连接 .
(1)、求抛物线的解析式;(2)、点为抛物线上一点,若 , 请直接写出点的坐标;(3)、点是抛物线上一点,若 , 求点的坐标.16. 如图,抛物线与x轴交于两点(A在B的左侧),与y轴交于点 , 点P在抛物线上,连接 . (1)、求抛物线的解析式;(2)、如图1,若点P在第四象限,点D在线段上,连接并延长交x轴于点E,连接 , 记的面积为 , 的面积为 , 当时,求点P的坐标;(3)、如图2,若点P在第二象限,点F为抛物线的顶点,抛物线的对称轴l与线段交于点G,当时,求点P的横坐标.17. 如图,已知直线y=x+4与x轴交于点A,与y轴交于点C,抛物线y=ax2+bx+c经过A,C两点,且与x轴的另一个交点为B,对称轴为直线x=﹣1.
(1)、求抛物线的解析式;(2)、如图1,若点P在第四象限,点D在线段上,连接并延长交x轴于点E,连接 , 记的面积为 , 的面积为 , 当时,求点P的坐标;(3)、如图2,若点P在第二象限,点F为抛物线的顶点,抛物线的对称轴l与线段交于点G,当时,求点P的横坐标.17. 如图,已知直线y=x+4与x轴交于点A,与y轴交于点C,抛物线y=ax2+bx+c经过A,C两点,且与x轴的另一个交点为B,对称轴为直线x=﹣1.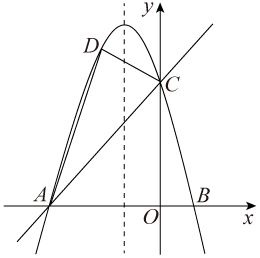 (1)、求抛物线的表达式;(2)、D是第二象限内抛物线上的动点,设点D的横坐标为m,求四边形ABCD面积S的最大值及此时D点的坐标;(3)、若点P在抛物线对称轴上,是否存在点P,Q,使以点A,C,P,Q为顶点的四边形是以AC为对角线的菱形?若存在,请求出P,Q两点的坐标;若不存在,请说明理由.18. 如图,抛物线交x轴于点和 , 交y轴于点C.
(1)、求抛物线的表达式;(2)、D是第二象限内抛物线上的动点,设点D的横坐标为m,求四边形ABCD面积S的最大值及此时D点的坐标;(3)、若点P在抛物线对称轴上,是否存在点P,Q,使以点A,C,P,Q为顶点的四边形是以AC为对角线的菱形?若存在,请求出P,Q两点的坐标;若不存在,请说明理由.18. 如图,抛物线交x轴于点和 , 交y轴于点C.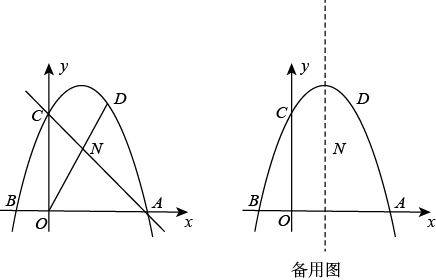 (1)、求抛物线的表达式;(2)、D是直线上方抛物线上一动点,连接交于点N,当的值最大时,求点D的坐标;(3)、P为抛物线上一点,连接 , 过点P作交抛物线对称轴于点Q,当时,请直接写出点P的横坐标.19. 如图,在平面直角坐标系中,抛物线与x轴分别交于点A(1,0)和点B,与y轴交于点C(0,﹣3),连接BC.
(1)、求抛物线的表达式;(2)、D是直线上方抛物线上一动点,连接交于点N,当的值最大时,求点D的坐标;(3)、P为抛物线上一点,连接 , 过点P作交抛物线对称轴于点Q,当时,请直接写出点P的横坐标.19. 如图,在平面直角坐标系中,抛物线与x轴分别交于点A(1,0)和点B,与y轴交于点C(0,﹣3),连接BC.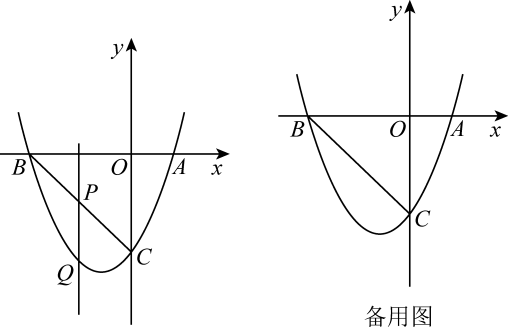 (1)、求抛物线的解析式及点B的坐标.(2)、如图,点P为线段BC上的一个动点(点P不与点B,C重合),过点P作y轴的平行线交抛物线于点Q,求线段PQ长度的最大值.(3)、动点P以每秒个单位长度的速度在线段BC上由点C向点B运动,同时动点M以每秒1个单位长度的速度在线段BO上由点B向点O运动,在平面内是否存在点N,使得以点P,M,B,N为顶点的四边形是菱形?若存在,请直接写出符合条件的点N的坐标;若不存在,请说明理由.20. 如图,抛物线与轴交于 , 两点,与轴交于点 , 连接 .
(1)、求抛物线的解析式及点B的坐标.(2)、如图,点P为线段BC上的一个动点(点P不与点B,C重合),过点P作y轴的平行线交抛物线于点Q,求线段PQ长度的最大值.(3)、动点P以每秒个单位长度的速度在线段BC上由点C向点B运动,同时动点M以每秒1个单位长度的速度在线段BO上由点B向点O运动,在平面内是否存在点N,使得以点P,M,B,N为顶点的四边形是菱形?若存在,请直接写出符合条件的点N的坐标;若不存在,请说明理由.20. 如图,抛物线与轴交于 , 两点,与轴交于点 , 连接 .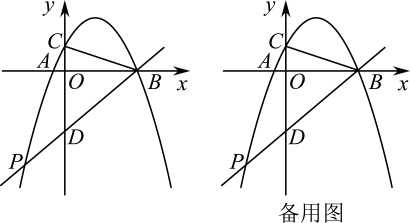 (1)、求抛物线的解析式.(2)、点是第三象限抛物线上一点,直线与轴交于点 , 的面积为12,求点的坐标.(3)、在(2)的条件下,若点是线段上点,连接 , 将沿直线翻折得到 , 当直线与直线相交所成锐角为时,求点的坐标.21. 如图,抛物线与x轴交于点 , 点 , 与y轴交于点C.
(1)、求抛物线的解析式.(2)、点是第三象限抛物线上一点,直线与轴交于点 , 的面积为12,求点的坐标.(3)、在(2)的条件下,若点是线段上点,连接 , 将沿直线翻折得到 , 当直线与直线相交所成锐角为时,求点的坐标.21. 如图,抛物线与x轴交于点 , 点 , 与y轴交于点C.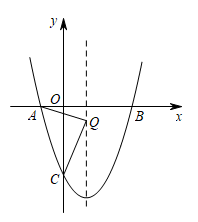 (1)、求抛物线的表达式;(2)、在对称轴上找一点Q,使的周长最小,求点Q的坐标;(3)、点P是抛物线对称轴上的一点,点M是对称轴左侧抛物线上的一点,当是以为腰的等腰直角三角形时,请直接写出所有点M的坐标.22. 如图,在平面直角坐标系中,已知抛物线的顶点为A,与y轴交于点C,线段轴,交该抛物线于另一点B.
(1)、求抛物线的表达式;(2)、在对称轴上找一点Q,使的周长最小,求点Q的坐标;(3)、点P是抛物线对称轴上的一点,点M是对称轴左侧抛物线上的一点,当是以为腰的等腰直角三角形时,请直接写出所有点M的坐标.22. 如图,在平面直角坐标系中,已知抛物线的顶点为A,与y轴交于点C,线段轴,交该抛物线于另一点B. (1)、求点B的坐标及直线的解析式:(2)、当二次函数的自变量x满足时,此函数的最大值为p,最小值为q,且.求m的值:(3)、平移抛物线 , 使其顶点始终在直线上移动,当平移后的抛物线与射线BA只有一个公共点时,设此时抛物线的顶点的横坐标为n,请直接写出n的取值范围.23. 如图,在平面直角坐标系中,抛物线( , 是常数)经过点 , 点 . 点在此抛物线上,其横坐标为 .
(1)、求点B的坐标及直线的解析式:(2)、当二次函数的自变量x满足时,此函数的最大值为p,最小值为q,且.求m的值:(3)、平移抛物线 , 使其顶点始终在直线上移动,当平移后的抛物线与射线BA只有一个公共点时,设此时抛物线的顶点的横坐标为n,请直接写出n的取值范围.23. 如图,在平面直角坐标系中,抛物线( , 是常数)经过点 , 点 . 点在此抛物线上,其横坐标为 . (1)、求此抛物线的解析式;(2)、当点在轴上方时,结合图象,直接写出的取值范围;(3)、若此抛物线在点左侧部分(包括点)的最低点的纵坐标为 .
(1)、求此抛物线的解析式;(2)、当点在轴上方时,结合图象,直接写出的取值范围;(3)、若此抛物线在点左侧部分(包括点)的最低点的纵坐标为 .①求的值;
②以为边作等腰直角三角形 , 当点在此抛物线的对称轴上时,直接写出点的坐标.
24. 如图,抛物线的对称轴是直线 , 与轴交于点 , , 与轴交于点 , 连接. (1)、求此抛物线的解析式;(2)、已知点是第一象限内抛物线上的一个动点,过点作轴,垂足为点 , 交直线于点 , 是否存在这样的点 , 使得以 , , 为顶点的三角形是等腰三角形.若存在,请求出点的坐标,若不存在,请说明理由;(3)、已知点是抛物线对称轴上的点,在坐标平面内是否存在点 , 使以点、、、为顶点的四边形为矩形,若存在,请直接写出点的坐标;若不存在,请说明理由.25. 如图,在平面直角坐标系中,抛物线与x轴交于A,B两点,与y轴交于点C,顶点为 , 抛物线的对称轴交直线于点E.
(1)、求此抛物线的解析式;(2)、已知点是第一象限内抛物线上的一个动点,过点作轴,垂足为点 , 交直线于点 , 是否存在这样的点 , 使得以 , , 为顶点的三角形是等腰三角形.若存在,请求出点的坐标,若不存在,请说明理由;(3)、已知点是抛物线对称轴上的点,在坐标平面内是否存在点 , 使以点、、、为顶点的四边形为矩形,若存在,请直接写出点的坐标;若不存在,请说明理由.25. 如图,在平面直角坐标系中,抛物线与x轴交于A,B两点,与y轴交于点C,顶点为 , 抛物线的对称轴交直线于点E. (1)、求抛物线的表达式;(2)、把上述抛物线沿它的对称轴向下平移,平移的距离为 , 在平移过程中,该抛物线与直线始终有交点,求h的最大值;(3)、M是(1)中抛物线上一点,N是直线上一点.是否存在以点D,E,M,N为顶点的四边形是平行四边形?若存在,求出点N的坐标;若不存在,请说明理由.26. 如图1,在平面直角坐标系中,抛物线:经过点和点.
(1)、求抛物线的表达式;(2)、把上述抛物线沿它的对称轴向下平移,平移的距离为 , 在平移过程中,该抛物线与直线始终有交点,求h的最大值;(3)、M是(1)中抛物线上一点,N是直线上一点.是否存在以点D,E,M,N为顶点的四边形是平行四边形?若存在,求出点N的坐标;若不存在,请说明理由.26. 如图1,在平面直角坐标系中,抛物线:经过点和点.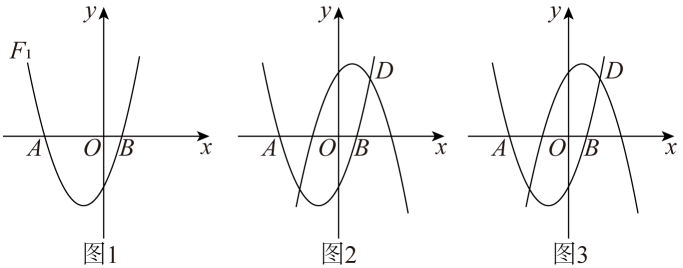 (1)、求抛物线的解析式;(2)、如图2,作抛物线 , 使它与抛物线关于原点成中心对称,请直接写出抛物线的解析式;(3)、如图3,将(2)中抛物线向上平移2个单位,得到抛物线 , 抛物线与抛物线相交于 , 两点(点在点的左侧).
(1)、求抛物线的解析式;(2)、如图2,作抛物线 , 使它与抛物线关于原点成中心对称,请直接写出抛物线的解析式;(3)、如图3,将(2)中抛物线向上平移2个单位,得到抛物线 , 抛物线与抛物线相交于 , 两点(点在点的左侧).①求点和点的坐标;
②若点 , 分别为抛物线和抛物线上 , 之间的动点(点 , 与点 , 不重合),试求四边形面积的最大值.
27. 如图,抛物线经过点 , 点 , 与y轴交于点C,抛物线的顶点为D. (1)、求抛物线的解析式;(2)、抛物线上是否存在点P,使的面积是面积的4倍,若存在,请直接写出点P的坐标:若不存在,请说明理由.28. 探索发现
(1)、求抛物线的解析式;(2)、抛物线上是否存在点P,使的面积是面积的4倍,若存在,请直接写出点P的坐标:若不存在,请说明理由.28. 探索发现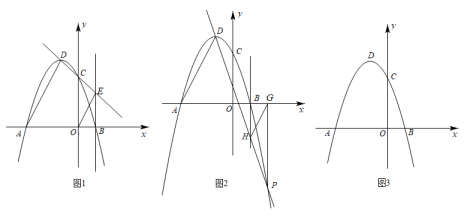 (1)、在平面直角坐标系中,抛物线y=ax2+bx+3(a≠0)与x轴交于点A(﹣3,0),B(1,0),与y轴交于点C,顶点为点D,连接AD.
(1)、在平面直角坐标系中,抛物线y=ax2+bx+3(a≠0)与x轴交于点A(﹣3,0),B(1,0),与y轴交于点C,顶点为点D,连接AD.①如图1,直线DC交直线x=1于点E,连接OE.求证:AD∥OE;
②如图2,点P(2,﹣5)为抛物线y=ax2+bx+3(a≠0)上一点,过点P作PG⊥x轴,垂足为点G.直线DP交直线x=1于点H,连接HG.求证:AD∥HG;
(2)、通过上述两种特殊情况的证明,你是否有所发现?请仿照(1)写出你的猜想,并在图3上画出草图.在平面直角坐标系中,抛物线y=ax2+bx+3(a≠0)与x轴交于点A(﹣3,0),B(1,0),顶点为点D.点M为该抛物线上一动点(不与点A,B,D重合),猜想:作MN⊥x轴于N,直线DM交直线x=1于Q,则QN∥AD,证明见解析
29. 综合与探究如图,某一次函数与二次函数的图象交点为A(-1,0),B(4,5).
 (1)、求抛物线的解析式;(2)、点C为抛物线对称轴上一动点,当AC与BC的和最小时,点C的坐标为 ;(3)、点D为抛物线位于线段AB下方图象上一动点,过点D作DE⊥x轴,交线段AB于点E,求线段DE长度的最大值;(4)、在(2)条件下,点M为y轴上一点,点F为直线AB上一点,点N为平面直角坐标系内一点,若以点C,M,F,N为顶点的四边形是正方形,请直接写出点N的坐标.30. 如图,抛物线交y轴于点 , 并经过点 , 过点A作轴交抛物线于点B,抛物线的对称轴为直线 , D点的坐标为 , 连接 , , .点E从A点出发,以每秒个单位长度的速度沿着射线运动,设点E的运动时间为m秒,过点E作于F,以为对角线作正方形 .
(1)、求抛物线的解析式;(2)、点C为抛物线对称轴上一动点,当AC与BC的和最小时,点C的坐标为 ;(3)、点D为抛物线位于线段AB下方图象上一动点,过点D作DE⊥x轴,交线段AB于点E,求线段DE长度的最大值;(4)、在(2)条件下,点M为y轴上一点,点F为直线AB上一点,点N为平面直角坐标系内一点,若以点C,M,F,N为顶点的四边形是正方形,请直接写出点N的坐标.30. 如图,抛物线交y轴于点 , 并经过点 , 过点A作轴交抛物线于点B,抛物线的对称轴为直线 , D点的坐标为 , 连接 , , .点E从A点出发,以每秒个单位长度的速度沿着射线运动,设点E的运动时间为m秒,过点E作于F,以为对角线作正方形 .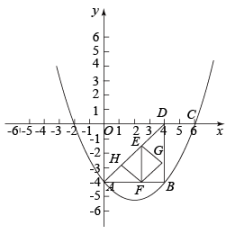
 (1)、求抛物线的解析式;(2)、当点G随着E点运动到达上时,求此时m的值和点G的坐标;(3)、在运动的过程中,是否存在以B,G,C和平面内的另一点为顶点的四边形是矩形,如果存在,直接写出点G的坐标,如果不存在,请说明理由.31. 如图,抛物线 (b,c是常数)的顶点为C,与x轴交于A,B两点, , ,点P为线段 上的动点,过P作 交 于点Q.
(1)、求抛物线的解析式;(2)、当点G随着E点运动到达上时,求此时m的值和点G的坐标;(3)、在运动的过程中,是否存在以B,G,C和平面内的另一点为顶点的四边形是矩形,如果存在,直接写出点G的坐标,如果不存在,请说明理由.31. 如图,抛物线 (b,c是常数)的顶点为C,与x轴交于A,B两点, , ,点P为线段 上的动点,过P作 交 于点Q. (1)、求该抛物线的解析式;(2)、求 面积的最大值,并求此时P点坐标.32. 抛物线与直线交于原点和点 , 与轴交于另一点 , 顶点为.
(1)、求该抛物线的解析式;(2)、求 面积的最大值,并求此时P点坐标.32. 抛物线与直线交于原点和点 , 与轴交于另一点 , 顶点为. (1)、直接写出点和点的坐标;(2)、如图1,连接 , 为轴上的动点,当时,求点的坐标;(3)、如图2,是点关于抛物线对称轴的对称点,是抛物线上的动点,它的横坐标为 , 连接 , , 与直线交于点设和的面积分别为和 , 求的最大值.33. 综合与探究
(1)、直接写出点和点的坐标;(2)、如图1,连接 , 为轴上的动点,当时,求点的坐标;(3)、如图2,是点关于抛物线对称轴的对称点,是抛物线上的动点,它的横坐标为 , 连接 , , 与直线交于点设和的面积分别为和 , 求的最大值.33. 综合与探究如图,二次函数的图象与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,点P是第一象限内二次函数图象上的一个动点,设点P的横坐标为m.过点P作直线轴于点D,作直线BC交PD于点E
 (1)、求A,B,C三点的坐标,并直接写出直线BC的函数表达式;(2)、当是以PE为底边的等腰三角形时,求点P的坐标;(3)、连接AC,过点P作直线 , 交y轴于点F,连接DF.试探究:在点P运动的过程中,是否存在点P,使得 , 若存在,请直接写出m的值;若不存在,请说明理由.34. 已知抛物线 与 轴交于 , 两点,与 轴交于点 .直线 由直线 平移得到,与 轴交于点 .四边形 的四个顶点的坐标分别为 , , , .
(1)、求A,B,C三点的坐标,并直接写出直线BC的函数表达式;(2)、当是以PE为底边的等腰三角形时,求点P的坐标;(3)、连接AC,过点P作直线 , 交y轴于点F,连接DF.试探究:在点P运动的过程中,是否存在点P,使得 , 若存在,请直接写出m的值;若不存在,请说明理由.34. 已知抛物线 与 轴交于 , 两点,与 轴交于点 .直线 由直线 平移得到,与 轴交于点 .四边形 的四个顶点的坐标分别为 , , , .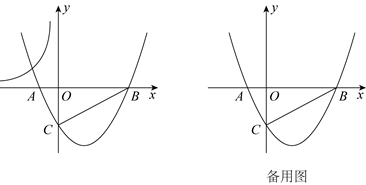 (1)、填空: , ;(2)、若点 在第二象限,直线 与经过点 的双曲线 有且只有一个交点,求 的最大值;(3)、当直线 与四边形 、抛物线 都有交点时,存在直线 ,对于同一条直线 上的交点,直线 与四边形 的交点的纵坐标都不大于它与抛物线 的交点的纵坐标.
(1)、填空: , ;(2)、若点 在第二象限,直线 与经过点 的双曲线 有且只有一个交点,求 的最大值;(3)、当直线 与四边形 、抛物线 都有交点时,存在直线 ,对于同一条直线 上的交点,直线 与四边形 的交点的纵坐标都不大于它与抛物线 的交点的纵坐标.①当 时,直接写出 的取值范围;
②求 的取值范围.
35. 已知抛物线y=x2+bx+c. (1)、如图①,若抛物线图象与x轴交于点A(3,0),与y轴交点B(0,﹣3),连接AB.
(1)、如图①,若抛物线图象与x轴交于点A(3,0),与y轴交点B(0,﹣3),连接AB.(Ⅰ)求该抛物线所表示的二次函数表达式;
(Ⅱ)若点P是抛物线上一动点(与点A不重合),过点P作PH⊥x轴于点H,与线段AB交于点M,是否存在点P使得点M是线段PH的三等分点?若存在,请求出点P的坐标:若不存在,请说明理由.
(2)、如图②,直线y= x+n与y轴交于点C,同时与抛物线y=x2+bx+c交于点D(﹣3,0),以线段CD为边作菱形CDFE,使点F落在x轴的正半轴上,若该抛物线与线段CE没有交点,求b的取值范围.36. 如图1,平面直角坐标系xOy中,抛物线与x轴分则点A和点 , 与y轴交于点C,对称轴为直线 , 且 , P为抛物线上一动点.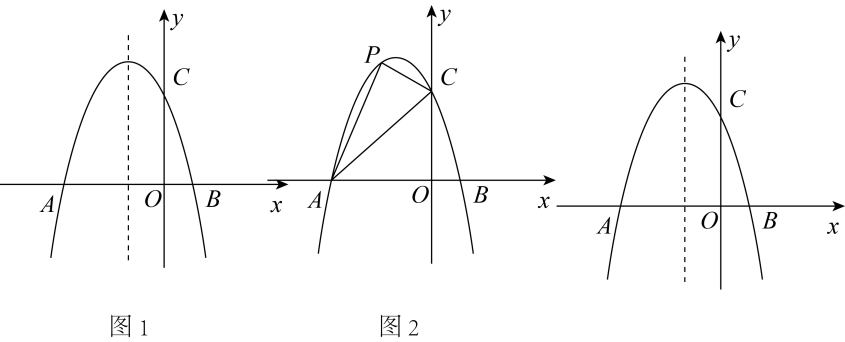 (1)、直接写出抛物线的解析式;(2)、如图2,连接AC,当点P在直线AC上方时,求四边形PABC面积的最大值,并求出此时P点的坐标;(3)、设M为抛物线对称轴上一动点,当P,M运动时,在坐标轴上是否存在点N,使四边形PMCN为矩形?若存在,直接写出点P及其对应点N的坐标;若不存在,请说明理由.37. 已知抛物线(a,b,c是常数,)的顶点为P,与x轴相交于点和点B.(1)、若 ,
(1)、直接写出抛物线的解析式;(2)、如图2,连接AC,当点P在直线AC上方时,求四边形PABC面积的最大值,并求出此时P点的坐标;(3)、设M为抛物线对称轴上一动点,当P,M运动时,在坐标轴上是否存在点N,使四边形PMCN为矩形?若存在,直接写出点P及其对应点N的坐标;若不存在,请说明理由.37. 已知抛物线(a,b,c是常数,)的顶点为P,与x轴相交于点和点B.(1)、若 ,①求点P的坐标;
②直线(m是常数,)与抛物线相交于点M,与相交于点G,当取得最大值时,求点M,G的坐标;
(2)、若 , 直线与抛物线相交于点N,E是x轴的正半轴上的动点,F是y轴的负半轴上的动点,当的最小值为5时,求点E,F的坐标.38. 如图,已知抛物线 交 轴于 、 两点,将该抛物线位于 轴下方的部分沿 轴翻折,其余部分不变,得到的新图象记为“图象 ”,图象 交 轴于点 .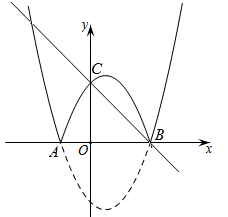 (1)、写出图象 位于线段 上方部分对应的函数关系式;(2)、若直线 与图象 有三个交点,请结合图象,直接写出 的值;(3)、 为 轴正半轴上一动点,过点 作 轴交直线 于点 ,交图象 于点 ,是否存在这样的点 ,使 与 相似?若存在,求出所有符合条件的点 的坐标;若不存在,请说明理由.39. 如图,在平面直角坐标系中,抛物线与x轴相交于点A、B(点A在点B的左侧),与y轴相交于点C,连接 .
(1)、写出图象 位于线段 上方部分对应的函数关系式;(2)、若直线 与图象 有三个交点,请结合图象,直接写出 的值;(3)、 为 轴正半轴上一动点,过点 作 轴交直线 于点 ,交图象 于点 ,是否存在这样的点 ,使 与 相似?若存在,求出所有符合条件的点 的坐标;若不存在,请说明理由.39. 如图,在平面直角坐标系中,抛物线与x轴相交于点A、B(点A在点B的左侧),与y轴相交于点C,连接 .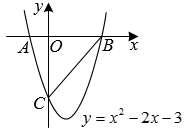 (1)、求线段AC的长;(2)、若点Р为该抛物线对称轴上的一个动点,当时,求点P的坐标;(3)、若点M为该抛物线上的一个动点,当为直角三角形时,求点M的坐标.40. 如图1,在平面直角坐标系中,已知二次函数 的图象经过点 , ,与y轴交于点C.
(1)、求线段AC的长;(2)、若点Р为该抛物线对称轴上的一个动点,当时,求点P的坐标;(3)、若点M为该抛物线上的一个动点,当为直角三角形时,求点M的坐标.40. 如图1,在平面直角坐标系中,已知二次函数 的图象经过点 , ,与y轴交于点C. (1)、求该二次函数的表达式;(2)、连接 ,在该二次函数图象上是否存在点P,使 ?若存在,请求出点P的坐标:若不存在,请说明理由;(3)、如图2,直线l为该二次函数图象的对称轴,交x轴于点E.若点Q为x轴上方二次函数图象上一动点,过点Q作直线 , 分别交直线l于点M,N,在点Q的运动过程中, 的值是否为定值?若是,请求出该定值;若不是,请说明理由.
(1)、求该二次函数的表达式;(2)、连接 ,在该二次函数图象上是否存在点P,使 ?若存在,请求出点P的坐标:若不存在,请说明理由;(3)、如图2,直线l为该二次函数图象的对称轴,交x轴于点E.若点Q为x轴上方二次函数图象上一动点,过点Q作直线 , 分别交直线l于点M,N,在点Q的运动过程中, 的值是否为定值?若是,请求出该定值;若不是,请说明理由.