2022年全国中考数学真题分类汇编14 二次函数实际应用-模型问题

试卷更新日期：2022-12-29 类型：二轮复习

进入出卷网下载

一、填空题

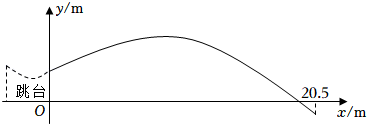
1. 在北京冬奥会自由式滑雪大跳台比赛中，我国选手谷爱凌的精彩表现让人叹为观止，已知谷爱凌从2m高的跳台滑出后的运动路线是一条抛物线，设她与跳台边缘的水平距离为xm，与跳台底部所在水平面的竖直高度为ym，y与x的函数关系式为y＝ $- \frac{1}{32}$ x²+ $\frac{1}{2}$ x+2（0≤x≤20.5），当她与跳台边缘的水平距离为m时，竖直高度达到最大值．

查看试题解析
2. 根据物理学规律，如果不考虑空气阻力，以 $40 m / s$ 的速度将小球沿与地面成 $30 °$ 角的方向击出，小球的飞行高度h（单位：m）与飞行时间t（单位：s）之间的函数关系是 $h = - 5 t^{2} + 20 t$ ，当飞行时间t为s时，小球达到最高点．

查看试题解析
3. 如图，是一名男生推铅球时，铅球行进过程中形成的抛物线．按照图中所示的平面直角坐标系，铅球行进高度y（单位：m）与水平距离x（单位：m）之间的关系是 $y = - \frac{1}{12} x^{2} + \frac{2}{3} x + \frac{5}{3}$ ，则铅球推出的水平距离OA的长是m．

查看试题解析
4. 如图是抛物线形拱桥，当拱顶离水面2米时，水面宽6米，水面下降米，水面宽8米.

查看试题解析
5. 如图，以一定的速度将小球沿与地面成一定角度的方向击出时，小球的飞行路线是一条抛物线.若不考虑空气阻力，小球的飞行高度 $h$ （单位：m）与飞行时间 $t$ （单位：s）之间具有函数关系： $h = - 5 t^{2} + 20 t$ ，则当小球飞行高度达到最高时，飞行时间 $t =$ s.

查看试题解析
6. 如图，一位篮球运动员投篮，球沿抛物线 $y = - 0.2 x^{2} + x + 2.25$ 运行，然后准确落入篮筐内，已知篮筐的中心离地面的高度为 3.05m ，则他距篮筐中心的水平距离 OH 是 m .

查看试题解析
7. 从喷水池喷头喷出的水珠，在空中形成一条抛物线，如图所示，在抛物线各个位置上，水珠的竖直高度 $y$ （单位： $m$ ）与它距离喷头的水平距离 $x$ （单位： $m$ ）之间满足函数关系式 $y = - 2 x^{2} + 4 x + 1$ ，喷出水珠的最大高度是 $m$ .

查看试题解析
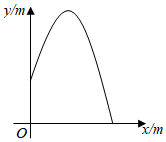8. 以初速度v（单位：m/s）从地面竖直向上抛出小球，从抛出到落地的过程中，小球的高度h（单位：m）与小球的运动时间t（单位：s）之间的关系式是h＝vt﹣4.9t².现将某弹性小球从地面竖直向上抛出，初速度为v₁ ，经过时间t₁落回地面，运动过程中小球的最大高度为h₁（如图1）；小球落地后，竖直向上弹起，初速度为v₂ ，经过时间t₂落回地面，运动过程中小球的最大高度为h₂（如图2）.若h₁＝2h₂ ，则t₁：t₂＝.

查看试题解析
9. 如图，抛物线 $y = a x^{2} + b x + c (a \neq 0)$ 与x轴交于点 $(- 1 ， 0)$ 和点 $(2 ， 0)$ ，以下结论：
① $a b c < 0$ ；② $4 a - 2 b + c < 0$ ；③ $a + b = 0$ ；④当 $x < \frac{1}{2}$ 时，y随x的增大而减小．其中正确的结论有．（填写代表正确结论的序号）

查看试题解析

二、解答题

10. 根据以下素材，探索完成任务．

如何设计拱桥景观灯的悬挂方案？
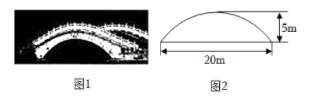
素材1	图1中有一座拱桥，图2是其抛物线形桥拱的示意图，某时测得水面宽 20m ，拱顶离水面 5m ．据调查，该河段水位在此基础上再涨 1.8m 达到最高．
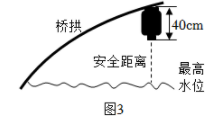
素材2	为迎佳节，拟在图1桥洞前面的桥拱上悬挂 40cm 长的灯笼，如图3．为了安全，灯笼底部距离水面不小于 1m ；为了实效，相邻两盏灯笼悬挂点的水平间距均为 1.6m ；为了美观，要求在符合条件处都挂上灯笼，且挂满后成轴对称分布．
问题解决
任务1	确定桥拱形状	在图2中建立合适的直角坐标系，求抛物线的函数表达式．
任务2	探究悬挂范围	在你所建立的坐标系中，仅在安全的条件下，确定悬挂点的纵坐标的最小值和横坐标的取值范围．
任务3	拟定设计方案	给出一种符合所有悬挂条件的灯笼数量，并根据你所建立的坐标系，求出最左边一盏灯笼悬挂点的横坐标．

查看试题解析

三、综合题

11. 掷实心球是兰州市高中阶段学校招生体育考试的选考项目．如图1是一名女生投掷实心球，实心球行进路线是一条抛物线，行进高度y（m）与水平距离x（m）之间的函数关系如图2所示，抛出时起点处高度为 $\frac{5}{3} m$ ，当水平距离为3m时，实心球行进至最高点3m处．

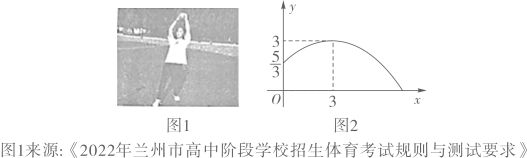(1)、求y关于x的函数表达式；

(2)、根据兰州市高中阶段学校招生体有考试评分标准（女生），投掷过程中，实心球从起点到落地点的水平距离大于等于6.70m，此项考试得分为满分10分．该女生在此项考试中是否得满分，请说明理由．

查看试题解析
12. 小红看到一处喷水景观，喷出的水柱呈抛物线形状，她对此展开研究：测得喷水头P距地面0.7m，水柱在距喷水头P水平距离5m处达到最高，最高点距地面3.2m；建立如图所示的平面直角坐标系，并设抛物线的表达式为 $y = a {(x - h)}^{2} + k$ ，其中x（m）是水柱距喷水头的水平距离，y（m）是水柱距地面的高度.

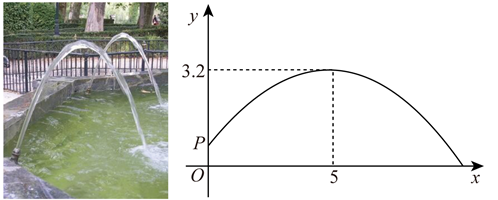(1)、求抛物线的表达式.

(2)、爸爸站在水柱正下方，且距喷水头P水平距离3m，身高1.6m的小红在水柱下方走动，当她的头顶恰好接触到水柱时，求她与爸爸的水平距离.

查看试题解析
13. 现要修建一条隧道，其截面为抛物线型，如图所示，线段 $O E$ 表示水平的路面，以O为坐标原点，以 $O E$ 所在直线为x轴，以过点O垂直于x轴的直线为y轴，建立平面直角坐标系.根据设计要求： $O E = 10 m$ ，该抛物线的顶点P到 $O E$ 的距离为 $9 m$ .

(1)、求满足设计要求的抛物线的函数表达式；

(2)、现需在这一隧道内壁上安装照明灯，如图所示，即在该抛物线上的点A、B处分别安装照明灯.已知点A、B到 $O E$ 的距离均为 $6 m$ ，求点A、B的坐标.

查看试题解析
14. 如图1，隧道截面由抛物线的一部分AED和矩形ABCD构成，矩形的一边BC为12米，另一边AB为2米．以BC所在的直线为x轴，线段BC的垂直平分线为y轴，建立平面直角坐标系xOy，规定一个单位长度代表1米．E（0，8）是抛物线的顶点．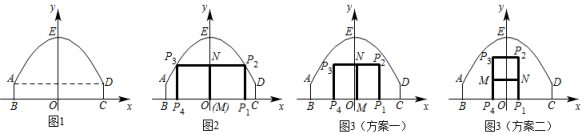

(1)、求此抛物线对应的函数表达式；

(2)、在隧道截面内（含边界）修建“”型或“”型栅栏，如图2、图3中粗线段所示，点 $P_{1}$ ， $P_{4}$ 在x轴上，MN与矩形 $P_{1} P_{2} P_{3} P_{4}$ 的一边平行且相等．栅栏总长l为图中粗线段 $P_{1} P_{2}$ ， $P_{2} P_{3}$ ， $P_{3} P_{4}$ ， MN长度之和．请解决以下问题：
（ⅰ）修建一个“”型栅栏，如图2，点 $P_{2}$ ， $P_{3}$ 在抛物线AED上．设点 $P_{1}$ 的横坐标为 $m (0 < m \leq 6)$ ，求栅栏总长l与m之间的函数表达式和l的最大值；
（ⅱ）现修建一个总长为18的栅栏，有如图3所示的修建“”型或“”型栅型两种设计方案，请你从中选择一种，求出该方案下矩形 $P_{1} P_{2} P_{3} P_{4}$ 面积的最大值，及取最大值时点 $P_{1}$ 的横坐标的取值范围（ $P_{1}$ 在 $P_{4}$ 右侧）．

查看试题解析
15. 甲秀楼是贵阳市一张靓丽的名片.如图①，甲秀楼的桥拱截面 $O B A$ 可视为抛物线的一部分，在某一时刻，桥拱内的水面宽 $O A = 8 m$ ，桥拱顶点 $B$ 到水面的距离是 $4m$ .

(1)、按如图②所示建立平面直角坐标系，求桥拱部分抛物线的函数表达式；

(2)、一只宽为 $1 .2m$ 的打捞船径直向桥驶来，当船驶到桥拱下方且距 $O$ 点 $0 .4m$ 时，桥下水位刚好在 $O A$ 处.有一名身高 $1.68 m$ 的工人站立在打捞船正中间清理垃圾，他的头顶是否会触碰到桥拱，请说明理由（假设船底与水面齐平）；

(3)、如图③，桥拱所在的函数图象是抛物线 $y = a x^{2} + b x + c (a \neq 0)$ ，该抛物线在 $x$ 轴下方部分与桥拱 $O B A$ 在平静水面中的倒影组成一个新函数图象.将新函数图象向右平移 $m (m > 0)$ 个单位长度，平移后的函数图象在 $8 \leq x \leq 9$ 时， $y$ 的值随 $x$ 值的增大而减小，结合函数图象，求 $m$ 的取值范围.

查看试题解析
16. 科研人员为了研究弹射器的某项性能，利用无人机测量小钢球竖直向上运动的相关数据．无人机上升到离地面30米处开始保持匀速竖直上升，此时，在地面用弹射器（高度不计）竖直向上弹射一个小钢球（忽路空气阻力），在1秒时，它们距离地面都是35米，在6秒时，它们距离地面的高度也相同．其中无人机离地面高度 $y_{1}$ （米）与小钢球运动时间 $x$ （秒）之间的函数关系如图所示；小钢球离地面高度 $y_{2}$ （米）与它的运动时间 $x$ （秒）之间的函数关系如图中抛物线所示．

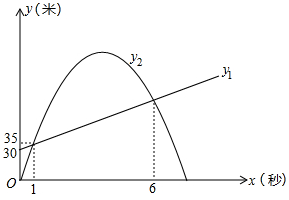(1)、直接写出 $y_{1}$ 与 $x$ 之间的函数关系式；

(2)、求出 $y_{2}$ 与 $x$ 之间的函数关系式；

(3)、小钢球弹射1秒后直至落地时，小钢球和无人机的高度差最大是多少米？

查看试题解析
17. 如图1是一座抛物线型拱桥侧面示意图.水面宽AB与桥长CD均为24m，在距离D点6米的E处，测得桥面到桥拱的距离EF为1.5m，以桥拱顶点O为原点，桥面为x轴建立平面直角坐标系.

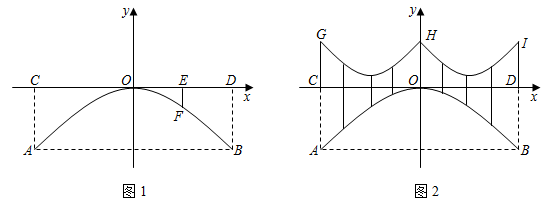(1)、求桥拱项部O离水面的距离.

(2)、如图2，桥面上方有3根高度均为4m的支柱CG，OH，DI，过相邻两根支柱顶端的钢缆呈形状相同的抛物线，其最低点到桥面距离为1m.
①求出其中一条钢缆抛物线的函数表达式.

②为庆祝节日，在钢缆和桥拱之间竖直装饰若干条彩带，求彩带长度的最小值.

查看试题解析
18. 某游乐场的圆形喷水池中心O有一雕塑OA，从A点向四周喷水，喷出的水柱为抛物线，且形状相同.如图，以水平方向为x轴，点O为原点建立直角坐标系，点A在y轴上，x轴上的点C，D为水柱的落水点，水柱所在抛物线第一象限部分的函数表达式为 $y = - \frac{1}{6} {(x - 5)}^{2} + 6$ .

(1)、求雕塑高OA.

(2)、求落水点C，D之间的距离.

(3)、若需要在OD上的点E处竖立雕塑EF， $O E = 10 m$ ， $E F = 1.8 m ， E F ⊥ O D$ .问：顶部F是否会碰到水柱？请通过计算说明.

查看试题解析
19. 第24届冬奥会（也称2022年北京冬奥会）于2022年2月4日至2月20日在中国北京举行，北京成为了历史上第一座既举办过夏奥会又举办过冬奥会的城市.冬奥会上跳台滑雪是一项极为壮观的运动.运动员经过助滑、起跳、空中飞行和着陆，整个动作连贯一致，一气呵成，如图，某运动员穿着滑雪板，经过助滑后，从倾斜角 $θ = 37 °$ 的跳台A点以速度 $v_{0}$ 沿水平方向跳出，若忽略空气阻力影响，水平方向速度将保持不变.同时，由于受重力作用，运动员沿竖直方向会加速下落，因此，运动员在空中飞行的路线是抛物线的一部分，已知该运动员在B点着陆， $A B = 150 m$ ，且 $s i n 37 ° = 0.6$ .忽略空气阻力，请回答下列问题：

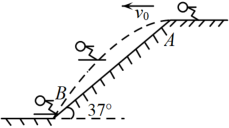(1)、求该运动员从跳出到着陆垂直下降了多少m？

(2)、以A为坐标原点建立直角坐标系，求该抛物线表达式；

(3)、若该运动员在空中共飞行了4s，求他飞行2s后，垂直下降了多少m？

查看试题解析
20. 如图1为北京冬奥会“雪飞天”滑雪大跳台赛道的横截面示意图．取水平线OE为x轴，铅垂线OD为y轴，建立平面直角坐标系．运动员以速度 $v (m / s)$ 从D点滑出，运动轨迹近似抛物线 $y = - a x^{2} + 2 x + 20 (a \neq 0)$ ．某运动员7次试跳的轨迹如图2．在着陆坡CE上设置点K（与DO相距32m）作为标准点，着陆点在K点或超过K点视为成绩达标．
（参考数据： $\sqrt{3} \approx 1.73$ ， $\sqrt{5} \approx 2.24$ ）

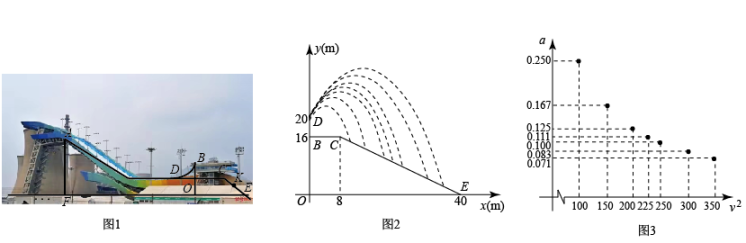(1)、求线段CE的函数表达式（写出 $x$ 的取值范围）．

(2)、当 $a = \frac{1}{9}$ 时，着陆点为P，求P的横坐标并判断成绩是否达标．

(3)、在试跳中发现运动轨迹与滑出速度v的大小有关，进一步探究，测算得7组a与 $v^{2}$ 的对应数据，在平面直角坐标系中描点如图3．
①猜想a关于 $v^{2}$ 的函数类型，求函数表达式，并任选一对对应值验证．

②当v为多少m/s时，运动员的成绩恰能达标（精确到1m/s)？

查看试题解析
21. 某校为配合疫情防控需要，每星期组织学生进行核酸抽样检测；防疫部门为了解学生错峰进入操场进行核酸检测情况，调查了某天上午学生进入操场的累计人数y（单位：人）与时间x（单位：分钟）的变化情况，发现其变化规律符合函数关系式： $y = {\begin{array}{l} a x^{2} + b x + c (0 \leq x \leq 8) \\ 640 ， (8 < x \leq 10) \end{array} ，$ 数据如下表．
时间x（分钟）
0
1
2
3
…
8
$8 < x ⩽ 10$
累计人数y（人）
0
150
280
390
…
640
640

(1)、求a，b，c的值；

(2)、如果学生一进入操场就开始排队进行核酸检测，检测点有4个，每个检测点每分钟检测5人，求排队人数的最大值（排队人数-累计人数-已检测人数）；

(3)、在（2）的条件下，全部学生都完成核酸检测需要多少时间？如果要在不超过20分钟让全部学生完成核酸检测，从一开始就应该至少增加几个检测点？

查看试题解析
22. $2022$ 北京冬奥会自由式滑雪空中技巧比赛中，某运动员比赛过程的空中剪影近似看作一条抛物线，跳台高度 $O A$ 为4米，以起跳点正下方跳台底端 $O$ 为原点，水平方向为横轴，竖直方向为纵轴，建立如图所示平面直角坐标系．已知抛物线最高点 $B$ 的坐标为 $(4 ， 12)$ ，着陆坡顶端 $C$ 与落地点 $D$ 的距离为2.5米，若斜坡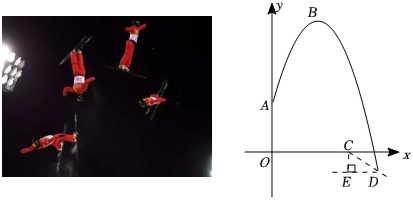 $C D$ 的坡度 $i = 3 ： 4$ （即 $\frac{C E}{D E} = \frac{3}{4}$ ）．求：

(1)、点 $A$ 的坐标；

(2)、该抛物线的函数表达式；

(3)、起跳点 $A$ 与着陆坡顶端 $C$ 之间的水平距离 $O C$ 的长．（精确到0.1米）（参考数据： $\sqrt{3} \approx 1.73$ ）

查看试题解析
23. 某市在盐碱地种植海水稻获得突破性进展，小亮和小莹到海水稻种植基地调研．小莹根据水稻年产量数据，分别在直角坐标系中描出表示2017-2021年①号田和②号田年产量情况的点（记2017年为第1年度，横轴表示年度，纵轴表示年产量），如下图．

小亮认为，可以从y=kx+b（k>0），y= $\frac{m}{x}$ （m>0），y=−0.1x²+ax+c中选择适当的函数模型，模拟①号田和②号田的年产量变化趋势．

(1)、小莹认为不能选 $y = \frac{m}{x} (m > 0)$ ．你认同吗？请说明理由；

(2)、请从小亮提供的函数模型中，选择适当的模型分别模拟①号田和②号田的年产量变化趋势，并求出函数表达式；

(3)、根据（2）中你选择的函数模型，请预测①号田和②号田总年产量在哪一年最大？最大是多少？

查看试题解析
24. 【生活情境】
为美化校园环境，某学校根据地形情况，要对景观带中一个长 $A D = 4 m$ ，宽 $A B = 1 m$ 的长方形水池 $A B C D$ 进行加长改造（如图①，改造后的水池 $A B N M$ 仍为长方形，以下简称水池1），同时，再建造一个周长为 $12 m$ 的矩形水池 $E F G H$ （如图②，以下简称水池2）．
【建立模型】
如果设水池 $A B C D$ 的边 $A D$ 加长长度 $D M$ 为 $x (m) (x > 0)$ ，加长后水池1的总面积为 $y_{1} (m^{2})$ ，则 $y_{1}$ 关于 $x$ 的函数解析式为： $y_{1} = x + 4 (x > 0)$ ；设水池2的边 $E F$ 的长为 $x (m) (0 < x < 6)$ ，面积为 $y_{2} (m^{2})$ ，则 $y_{2}$ 关于 $x$ 的函数解析式为： $y_{2} = - x^{2} + 6 x (0 < x < 6)$ ，上述两个函数在同一平面直角坐标系中的图像如图③．
【问题解决】

(1)、若水池2的面积随 $E F$ 长度的增加而减小，则 $E F$ 长度的取值范围是（可省略单位），水池2面积的最大值是 $m^{2}$ ；

(2)、在图③字母标注的点中，表示两个水池面积相等的点是，此时的 $x (m)$ 值是；

(3)、当水池1的面积大于水池2的面积时， $x (m)$ 的取值范围是；

(4)、在 $1 < x < 4$ 范围内，求两个水池面积差的最大值和此时 $x$ 的值；

(5)、假设水池 $A B C D$ 的边 $A D$ 的长度为 $b (m)$ ，其他条件不变（这个加长改造后的新水池简称水池3），则水池3的总面积 $y_{3} (m^{2})$ 关于 $x (m) (x > 0)$ 的函数解析式为： $y_{3} = x + b (x > 0)$ ．若水池3与水池2的面积相等时， $x (m)$ 有唯一值，求 $b$ 的值．

查看试题解析
25. 单板滑雪大跳台是北京冬奥会比赛项目之一，举办场地为首钢滑雪大跳台，运动员起跳后的飞行路线可以看作是抛物线的一部分，建立如图所示的平面直角坐标系，从起跳到着陆的过程中，运动员的竖直高度 $y$ （单位：m）与水平距离 $x$ （单位：m）近似满足函数关系 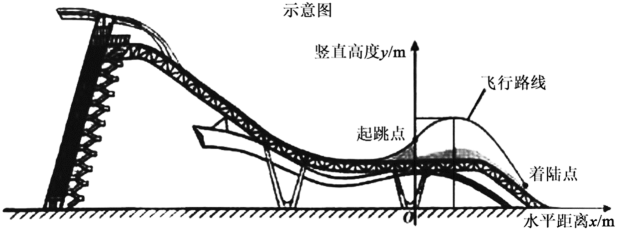$y = a (x - h)^{2} + k (a < 0)$ ．
某运动员进行了两次训练．

(1)、第一次训练时，该运动员的水平距离 $x$ 与竖直高度 $y$ 的几组数据如下：
水平距离x/m
0
2
5
8
11
14
竖直高度y/m
20.00
21.40
22.75
23.20
22.75
21.40
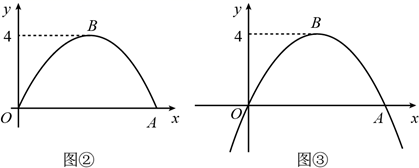
根据上述数据，直接写出该运动员竖直高度的最大值，并求出满足的函数关系 $y = a (x - h)^{2} + k (a < 0) ；$

(2)、第二次训练时，该运动员的竖直高度y与水平距离x近似满足函数关系 $y = - 0.04 (x - 9)^{2} + 23.24 .$ 记该运动员第一次训练的着陆点的水平距离为d₁ ，第二次训练的着陆点的水平距离为 $d_{2}$ ，则 $d_{1}$ $d_{2}$ （填“>”“=”或“<”）．

查看试题解析
26. 如图，点 $P (a ， 3)$ 在抛物线C： $y = 4 - {(6 - x)}^{2}$ 上，且在C的对称轴右侧．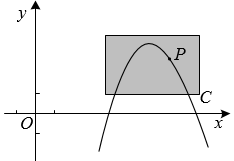

(1)、写出C的对称轴和y的最大值，并求a的值；

(2)、坐标平面上放置一透明胶片，并在胶片上描画出点P及C的一段，分别记为 $P^{'}$ ， $C^{'}$ ．平移该胶片，使 $C^{'}$ 所在抛物线对应的函数恰为 $y = - x^{2} + 6 x - 9$ ．求点 $P^{'}$ 移动的最短路程．

查看试题解析
27. 为落实国家《关于全面加强新时代大中小学劳动教育的意见》，某校准备在校园里利用围墙（墙长12m）和21m长的篱笆墙，围成I、Ⅱ两块矩形劳动实践基地.某数学兴趣小组设计了两种方案（除围墙外，实线部分为篱笆墙，且不浪费篱笆墙），请根据设计方案回答下列问题：

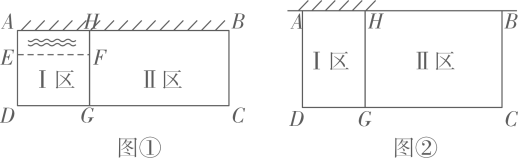(1)、方案一：如图①，全部利用围墙的长度，但要在I区中留一个宽度AE=1m的水池，且需保证总种植面积为32m² ，试分别确定CG、DG的长；

(2)、方案二：如图②，使围成的两块矩形总种植面积最大，请问BC应设计为多长？此时最大面积为多少？

查看试题解析

28. 在一条笔直的滑道上有黑、白两个小球同向运动，黑球在

A

处开始减速，此时白球在黑球前面

70 c m

处.

小聪测量黑球减速后的运动速度 $v$ （单位： $c m / s$ ）、运动距离 $y$ （单位： $c m$ ）随运动时间 $t$ （单位： $s$ ）变化的数据，整理得下表.

运动时间 $t / s$	0	1	2	3	4
运动速度 $v / c m / s$	10	9.5	9	8.5	8
运动距离 $y / c m$	0	9.75	19	27.75	36

小聪探究发现，黑球的运动速度 $v$ 与运动时间 $t$ 之间成一次函数关系，运动距离 $y$ 与运动时间 $t$ 之间成二次函数关系.

(1)、直接写出

v

关于

t

的函数解析式和

y

关于

t

的函数解析式（不要求写出自变量的取值范围）

(2)、当黑球减速后运动距离为

64 c m

时，求它此时的运动速度；

(3)、若白球一直以

2 c m / s

的速度匀速运动，问黑球在运动过程中会不会碰到白球？请说明理由.

查看试题解析

29. 跳台滑雪运动可分为助滑、起跳、飞行和落地四个阶段，运动员起跳后飞行的路线是抛物线的一部分（如图中实线部分所示），落地点在着陆坡（如图中虚线部分所示）上，着陆坡上的基准点K为飞行距离计分的参照点，落地点超过K点越远，飞行距离分越高.2022年北京冬奥会跳台滑雪标准台的起跳台的高度 $O A$ 为 $66 m$ ，基准点K到起跳台的水平距离为 $75 m$ ，高度为 $h m$ （h为定值）．设运动员从起跳点A起跳后的高度 $y (m)$ 与水平距离 $x (m)$ 之间的函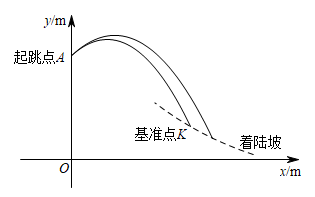数关系为 $y = a x^{2} + b x + c (a \neq 0)$ ．

(1)、c的值为；

(2)、①若运动员落地点恰好到达K点，且此时 $a = - \frac{1}{50} ， b = \frac{9}{10}$ ，求基准点K的高度h；
②若 $a = - \frac{1}{50}$ 时，运动员落地点要超过K点，则b的取值范围为_▲_；

(3)、若运动员飞行的水平距离为 $25 m$ 时，恰好达到最大高度 $76 m$ ，试判断他的落地点能否超过K点，并说明理由．

查看试题解析
30. 如图1，灌溉车沿着平行于绿化带底部边线l的方向行驶，为绿化带浇水．喷水口H离地竖直高度为h（单位： m）．如图2，可以把灌溉车喷出水的上、下边缘抽象为平面直角坐标系中两条抛物线的部分图象；把绿化带横截面抽象为矩形 DEFG ，其水平宽度DE=3m，竖直高度为EF的长．下边缘抛物线是由上边缘抛物线向左平移得到，上边缘抛物线最高点A离喷水口的水平距离为2m，高出喷水口0.5m，灌溉车到l 的距离OD为d（单位：m）．

(1)、若h=1.5，EF=0.5m；
①求上边缘抛物线的函数解析式，并求喷出水的最大射程 OC；

②求下边缘抛物线与x 轴的正半轴交点B的坐标；

③要使灌溉车行驶时喷出的水能浇灌到整个绿化带，求d的取值范围；

(2)、若 EF=1m．要使灌溉车行驶时喷出的水能浇灌到整个绿化带，请直接写出h的最小值．

查看试题解析

时间x（分钟）	0	1	2	3	…	8	$8 < x ⩽ 10$
累计人数y（人）	0	150	280	390	…	640	640

水平距离x/m	0	2	5	8	11	14
竖直高度y/m	20.00	21.40	22.75	23.20	22.75	21.40