2022年全国中考数学真题分类汇编13 二次函数实际应用-销售问题

试卷更新日期：2022-12-29 类型：二轮复习

进入出卷网下载

一、填空题

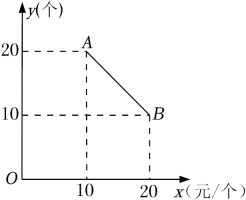
1. 某食品零售店新上架一款冷饮产品，每个成本为8元，在销售过程中，每天的销售量y（个）与销售价格x（元/个）的关系如图所示，当 $10 ≤ x ≤ 20$ 时，其图象是线段AB，则该食品零售店每天销售这款冷饮产品的最大利润为元（利润=总销售额-总成本）．

查看试题解析
2. 某超市购进一批单价为8元的生活用品，如果按每件9元出售，那么每天可销售20件．经调查发现，这种生活用品的销售单价每提高1元，其销售量相应减少4件，那么将销售价定为元时，才能使每天所获销售利润最大．

查看试题解析
3. 某快餐店销售A、B两种快餐，每份利润分别为12元、8元，每天卖出份数分别为40份、80份.该店为了增加利润，准备降低每份A种快餐的利润，同时提高每份B种快餐的利润.售卖时发现，在一定范围内，每份A种快餐利润每降1元可多卖2份，每份B种快餐利润每提高1元就少卖2份.如果这两种快餐每天销售总份数不变，那么这两种快餐一天的总利润最多是元.

查看试题解析

二、综合题

4. 端午节前夕，某超市从厂家分两次购进 $A$ 、 $B$ 两种品牌的粽子，两次进货时，两种品牌粽子的进价不变.第一次购进 $A$ 品牌粽子100袋和 $B$ 品牌粽子150袋，总费用为7000元；第二次购进 $A$ 品牌粽子180袋和 $B$ 品牌粽子120袋，总费用为8100元.

(1)、求 $A$ 、 $B$ 两种品牌粽子每袋的进价各是多少元；

(2)、当 $B$ 品牌粽子销售价为每袋54元时，每天可售出20袋，为了促销，该超市决定对 $B$ 品牌粽子进行降价销售.经市场调研，若每袋的销售价每降低1元，则每天的销售量将增加5袋.当 $B$ 品牌粽子每袋的销售价降低多少元时，每天售出 $B$ 品牌粽子所获得的利润最大？最大利润是多少元？

查看试题解析
5. 端午节吃粽子是中华民族的传统习俗，市场上猪肉粽进价比豆沙粽进价每盒贵10元，一盒猪肉粽加两盒豆沙粽进价为100元．

(1)、求每盒猪肉粽和豆沙粽的进价；

(2)、在销售中，某商家发现当每盒猪肉粽售价为50元时，每天可售出100盒，若每盒售价提高1元，则每天少售出2盒．设每盒猪肉粽售价为 $a$ 元，销售猪肉粽的利润为 $w$ 元，求该商家每天销售猪肉粽获得的最大利润．

查看试题解析
6. 丹东是我国的边境城市，拥有丰富的旅游资源．某景区研发一款纪念品，每件成本为30元，投放景区内进行销售，规定销售单价不低于成本且不高于54元，销售一段时间调研发现，每天的销售数量y（件）与销售单价x（元/件）满足一次函数关系，部分数据如下表所示：
销售单价x（元/件）
…
35
40
45
…
每天销售数量y（件）
…
90
80
70
…

(1)、直接写出y与x的函数关系式；

(2)、若每天销售所得利润为1200元，那么销售单价应定为多少元？

(3)、当销售单价为多少元时，每天获利最大？最大利润是多少元？

查看试题解析
7. 某商场新进一批拼装玩具，进价为每个10元，在销售过程中发现．，日销售量y（个）与销售单价x（元）之间满足如图所示的一次函数关系．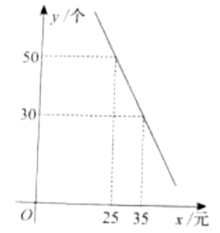

(1)、求y与x的函数关系式（不要求写出自变量x的取值范围）；

(2)、若该玩具某天的销售利润是600元，则当天玩具的销售单价是多少元？

(3)、设该玩具日销售利润为w元，当玩具的销售单价定为多少元时，日销售利润最大？最大利润是多少元？

查看试题解析
8. 某超市购进一批水果，成本为8元/ $k g$ ，根据市场调研发现，这种水果在未来10天的售价 $m$ （元/ $k g$ ）与时间第 $x$ 天之间满足函数关系式 $m = \frac{1}{2} x + 18$ （ $1 \leq x \leq 10$ ， $x$ 为整数），又通过分析销售情况，发现每天销售量 $y (k g)$ 与时间第 $x$ 天之间满足一次函数关系，下表是其中的三组对应值．
时间第 $x$ 天
…
2
5
9
…
销售量 $y / k g$
…
33
30
26
…

(1)、求 $y$ 与 $x$ 的函数解析式；

(2)、在这10天中，哪一天销售这种水果的利润最大，最大销售利润为多少元？

查看试题解析
9. 某文具店购进一批单价为12元的学习用品，按照相关部门规定其销售单价不低于进价，且不高于进价的1.5倍，通过分析销售情况，发现每天的销售量y（件）与销售单价x（元）满足一次函数关系，且当 $x = 15$ 时， $y = 50$ ；当 $x = 17$ 时， $y = 30$ ．

(1)、求y与x之间的函数关系式；

(2)、这种学习用品的销售单价定为多少时，每天可获得最大利润，最大利润是多少元？

查看试题解析
10. 某商店购进了一种消毒用品，进价为每件8元，在销售过程中发现，每天的销售量y（件）与每件售价x（元）之间存在一次函数关系（其中8≤x≤15，且x为整数）．当每件消毒用品售价为9元时，每天的销售量为105件；当每件消毒用品售价为11元时，每天的销售量为95件．

(1)、求y与x之间的函数关系式．

(2)、若该商店销售这种消毒用品每天获得425元的利润，则每件消毒用品的售价为多少元？

(3)、设该商店销售这种消毒用品每天获利w（元），当每件消毒用品的售价为多少元时，每天的销售利润最大？最大利润是多少元？

查看试题解析
11. 某超市销售一种进价为18元/千克的商品，经市场调查后发现，每天的销售量y（千克）与销售单价x（元/千克）有如下表所示的关系：
销售单价x（元/千克）
…
20
22.5
25
37.5
40
…
销售量y（千克）
…
30
27.5
25
12.5
10
…

(1)、根据表中的数据在下图中描点 $(x ， y)$ ，并用平滑曲线连接这些点，请用所学知识求出y关于x的函数关系式；

(2)、设该超市每天销售这种商品的利润为w（元）（不计其它成本），
①求出w关于x的函数关系式，并求出获得最大利润时，销售单价为多少；
②超市本着“尽量让顾客享受实惠”的销售原则，求 $w = 240$ （元）时的销售单价.

查看试题解析
12. 2022年在中国举办的冬奥会和残奥会令世界瞩目，冬奥会和残奥会的吉祥物冰墩墩和雪容融家喻户晓，成为热销产品，某商家以每套34元的价格购进一批冰墩墩和雪容融套件，若该产品每套的售价是48元时，每天可售出200套；若每套售价提高2元，则每天少卖4套.

(1)、设冰墩墩和雪容融套件每套售价定为x元时，求该商品销售量y与x之间的函数关系式；

(2)、求每套售价定为多少元时，每天销售套件所获利润W最大，最大利润是多少元？

查看试题解析
13. 打油茶是广西少数民族特有的一种民俗，某特产公司近期销售一种盒装油茶，每盒的成本价为50元，经市场调研发现，该种油茶的月销售量y（盒）与销售单价x（元）之间的函数图象如图所示.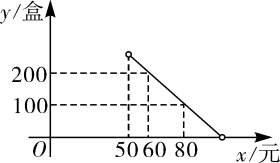

(1)、求y与x的函数解析式，并写出自变量x的取值范围；

(2)、当销售单价定为多少元时，该种油茶的月销售利润最大?求出最大利润.

查看试题解析
14. 某商户购进一批童装，40天销售完毕.根据所记录的数据发现，日销售量 $y$ （件）与销售时间 $x$ （天）之间的关系式是 $y = {\begin{cases} 2 x ， 0 < x \leq 30 \\ - 6 x + 240 ， 30 < x \leq 40 \end{cases}$ ，销售单价 $p$ （元/件）与销售时间 $x$ （天）之间的函数关系如图所示.

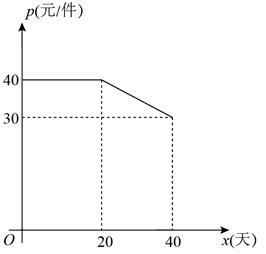(1)、第15天的日销售量为件；

(2)、当 $0 < x \leq 30$ 时，求日销售额的最大值；

(3)、在销售过程中，若日销售量不低于48件的时间段为“火热销售期”，则“火热销售期”共有多少天？

查看试题解析
15. 某企业投入60万元（只计入第一年成本）生产某种产品，按网上订单生产并销售（生产量等于销售量）.经测算，该产品网上每年的销售量y（万件）与售价x（元/件）之间满足函数关系式y＝24－x，第一年除60万元外其他成本为8元/件.

(1)、求该产品第一年的利润w（万元）与售价x之间的函数关系式；

(2)、该产品第一年利润为4万元，第二年将它全部作为技改资金再次投入（只计入第二年成本）后，其他成本下降2元/件.①求该产品第一年的售价；②若第二年售价不高于第一年，销售量不超过13万件，则第二年利润最少是多少万元？

查看试题解析

16. 2022年的冬奥会在北京举行，其中冬奥会古祥物“冰墩墩”深受人们喜爱，多地出现了“一墩难求”的场面，某纪念品商店在开始售卖当天提供150个“冰墩墩”后很快就被抢购一空.该店决定让当天未购买到的顾客可通过预约在第二天优先购买，并且从第二天起，每天比前一天多供应m个（m为正整数）经过连续15天的销售统计，得到第x天（

1 \leq x \leq 15

，且x为正整数）的供应量

y_{1}

（单位：个）和需求量

y_{2}

（单位：个）的部分数据如下表，其中需求量

y_{2}

与x满足某二次函数关系.（假设当天预约的顾客第二天都会购买，当天的需求量不包括前一天的预约数）

第x天	1	2	…	6	…	11	…	15
供应量 $y_{1}$ （个）	150	$150 + m$	…	$150 + 5 m$	…	$150 + 10 m$	…	$150 + 14 m$
需求量 $y_{2}$ （个）	220	229	…	245	…	220	…	164

(1)、直接写出

y_{1}

与x和

y_{2}

与x的函数关系式；（不要求写出x的取值范围）

(2)、已知从第10天开始，有需求的顾客都不需要预约就能购买到（即前9天的总需求量超过总供应量，前10天的总需求量不超过总供应量），求m的值；（参考数据：前9天的总需求量为2136个）

(3)、在第（2）问m取最小值的条件下，若每个“冰墩墩”售价为100元，求第4天与第12天的销售额.

查看试题解析

17. 某种商品每件的进价为10元，若每件按20元的价格销售，则每月能卖出360件；若每件按30元的价格销售，则每月能卖出60件．假定每月的销售件数y是销售价格x（单位：元）的一次函数．

(1)、求y关于x的一次函数解析式；

(2)、当销售价格定为多少元时，每月获得的利润最大？并求此最大利润．

查看试题解析

18. “八婺”菜场指导菜农生产和销售某种蔬菜，提供如下信息：

①统计售价与需求量的数据，通过描点(图1)，发现该蔬菜需求量y_需求(吨)关于售价x(元/千克)的函数图象可以看成抛物线，其表达式为 $y_{需求} = a x^{2} + c$ ，部分对应值如下表：

售价x(元/千克)	…	2.5	3	3.5	4	…
需求量y_需求(吨）	…	7.75	7.2	6.55	5.8	…

②该蔬菜供给量y_供给(吨)关于售价x(元/千克)的函数表达式为y_供给=x-1，函数图象见图1.

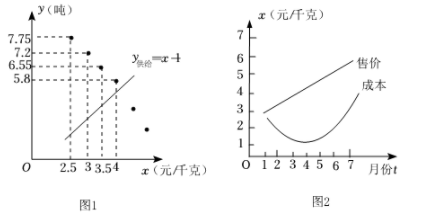
③1~7月份该蔬菜售价x_售价(元/千克)、成本x_成本(元/千克)关于月份t的函数表达式分别为 $x_{售价} = \frac{1}{2} t + 2$ ， $x_{成本} = \frac{1}{4} t^{2} - \frac{3}{2} t + 3$ ，函数图象见图2.

请解答下列问题：

(1)、求a，c的值.

(2)、根据图2，哪个月出售这种蔬菜每千克获利最大？并说明理由.

(3)、求该蔬菜供给量与需求量相等时的售价，以及按此价格出售获得的总利润.

查看试题解析

19. 农技人员对培育的某一品种桃树进行研究，发现桃子成熟后一棵树上每个桃子质量大致相同.以每棵树上桃子的数量x（个）为横坐标、桃子的平均质量y（克/个）为纵坐标，在平面直角坐标系中描出对应的点，发现这些点大致分布在直线AB附近（如图所示）.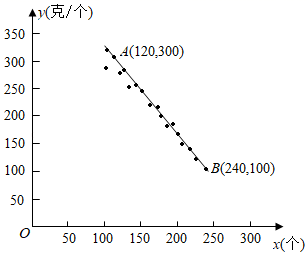

(1)、求直线AB的函数关系式；

(2)、市场调研发现：这个品种每个桃子的平均价格w（元）与平均质量y（克/个）满足函数表达式w＝ $\frac{1}{100}$ y+2.在（1）的情形下，求一棵树上桃子数量为多少时，该树上的桃子销售额最大？

查看试题解析
20. 某公司电商平台，在2021年五一长假期间，举行了商品打折促销活动，经市场调查发现，某种商品的周销售量y（件）是关于售价x（元/件）的一次函数，下表仅列出了该商品的售价x，周销售量y，周销售利润W（元）的三组对应值数据.

x

40

70

90

y

180

90

30

W

3600

4500

2100

(1)、求y关于x的函数解析式（不要求写出自变量的取值范围）；

(2)、若该商品进价a（元/件），售价x为多少时，周销售利润W最大？并求出此时的最大利润；

(3)、因疫情期间，该商品进价提高了m（元/件）（ $m > 0$ ），公司为回馈消费者，规定该商品售价x不得超过55（元/件），且该商品在今后的销售中，周销售量与售价仍满足（1）中的函数关系，若周销售最大利润是4050元，求m的值.

查看试题解析
21. 某商店从厂家以每件2元的价格购进一批商品，在市场试销中发现，此商品的月销售量y（单位：万件）与销售单价x（单位元）之间有如下表所示关系：

x

…

4.0

5.0

5.5

6.5

7.5

…

y

…

8.0

6.0

5.0

3.0

1.0

…

(1)、根据表中的数据，在如图中描出实数对（x，y）所对应的点，并画出y关于x的函数图象；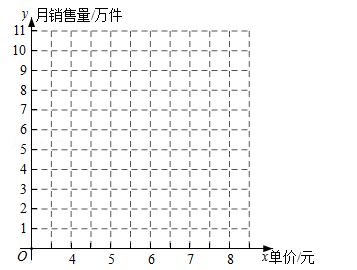

(2)、根据画出的函数图象，求出y关于x的函数表达式；

(3)、设经营此商品的月销售利润为P（单位：万元），
①写出P关于x的函数表达式；

②该商店计划从这批商品获得的月销售利润为10万元（不计其它成本），若物价局限定商品的销售单价不得超过进价的200%，则此时的销售单价应定为多少元？

查看试题解析
22. 某药店选购了一批消毒液，进价为每瓶10元，在销售过程中发现销售量y（瓶）与每瓶售价x（元）之间存在一次函数关系（其中 $10 \leq x \leq 21$ ，且x为整数），当每瓶消毒液售价为12元时，每天销售量为90瓶；当每瓶消毒液售价为15元时，每天销售量为75瓶；

(1)、求y与x之间的函数关系式；

(2)、设该药店销售该消毒液每天的销售利润为w元，当每瓶消毒液售价为多少元时，药店销售该消毒液每天销售利润最大.

查看试题解析

23. 去年“抗疫”期间，某生产消毒液厂家响应政府号召，将成本价为6元/件的简装消毒液低价销售.为此当地政府决定给予其销售的这种消毒液按a元/件进行补贴，设某月销售价为x元/件，a与x之间满足关系式：

a = 20 % (10 - x)

，下表是某4个月的销售记录.每月销售量

y

（万件）与该月销售价x（元/件）之间成一次函数关系

(6 \leq x < 9)

月份	…	二月	三月	四月	五月	…
销售价x（元件）	…	6	7	7.6	8.5	…
该月销售量y（万件）	…	30	20	14	5	…

(1)、求y与x的函数关系式；

(2)、当销售价为8元/件时，政府该月应付给厂家补贴多少万元？

(3)、当销售价x定为多少时，该月纯收入最大？（纯收入=销售总金额-成本+政府当月补贴）

查看试题解析

24. 某超市经销一种商品，每件成本为50元.经市场调研，当该商品每件的销售价为60元时，每个月可销售300件，若每件的销售价每增加1元，则每个月的销售量将减少10件.设该商品每件的销售价为x元，每个月的销售量为y件.

(1)、求y与x的函数表达式；

(2)、当该商品每件的销售价为多少元时，每个月的销售利润最大？最大利润是多少？

查看试题解析
25. 为增加农民收入，助力乡村振兴.某驻村干部指导农户进行草莓种植和销售，已知草莓的种植成本为8元/千克，经市场调查发现，今年五一期间草莓的销售量y（千克）与销售单价x（元/千克）（8≤x≤40）满足的函数图象如图所示.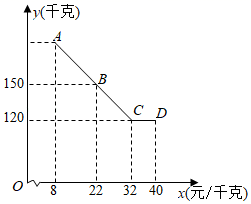

(1)、根据图象信息，求y与x的函数关系式；

(2)、求五一期间销售草莓获得的最大利润.

查看试题解析
26. 某品牌汽车销售店销售某种品牌的汽车，每辆汽车的进价16（万元）.当每辆售价为22（万元）时，每月可销售4辆汽车.根据市场行情，现在决定进行降价销售.通过市场调查得到了每辆降价的费用 $y_{1}$ （万元）与月销售量 $x$ （辆）（ $x \geq 4$ ）满足某种函数关系的五组对应数据如下表：

$x$

4

5

6

7

8

$y_{1}$

0

0.5

1

1.5

2

(1)、请你根据所给材料和初中所学的函数知识写出 $y_{1}$ 与 $x$ 的关系式 $y_{1} =$ ；

(2)、每辆原售价为22万元，不考虑其它成本，降价后每月销售利润y=(每辆原售价- $y_{1}$ -进价)x，请你根据上述条件，求出月销售量 $x (x \geq 4)$ 为多少时，销售利润最大？最大利润是多少？

查看试题解析
27. 某工厂生产并销售A ， B两种型号车床共14台，生产并销售1台A型车床可以获利10万元；如果生产并销售不超过4台B型车床，则每台B型车床可以获利17万元，如果超出4台B型车床，则每超出1台，每台B型车床获利将均减少1万元．设生产并销售B型车床 $x$ 台．

(1)、当 $x > 4$ 时，完成以下两个问题：
①请补全下面的表格：

A型

B型

车床数量/台

▲

$x$

每台车床获利/万元

10

▲

②若生产并销售B型车床比生产并销售A型车床获得的利润多70万元，问：生产并销售B型车床多少台？

(2)、当0＜ $x$ ≤14时，设生产并销售A ， B两种型号车床获得的总利润为W万元，如何分配生产并销售A ， B两种车床的数量，使获得的总利润W最大？并求出最大利润．

查看试题解析
28. 某公司计划购进一批原料加工销售，已知该原料的进价为6.2万元/t ，加工过程中原料的质量有20%的损耗，加工费m（万元）与原料的质量x（t）之间的关系为m＝50＋0.2x ，销售价y（万元/t）与原料的质量x（t）之间的关系如图所示．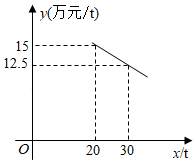

(1)、求y与x之间的函数关系式；

(2)、设销售收入为P（万元），求P与x之间的函数关系式；

(3)、原料的质量x为多少吨时，所获销售利润最大，最大销售利润是多少万元？（销售利润＝销售收入﹣总支出）．

查看试题解析
29. 某商场以每件20元的价格购进一种商品，规定这种商品每件售价不低于进价，又不高于38元，经市场调查发现：该商品每天的销售量y（件）与每件售价（元）之间符合一次函数关系，如图所示．

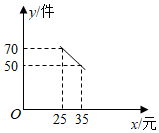(1)、求y与x之间的函数关系式；

(2)、该商场销售这种商品要想每天获得600元的利润，每件商品的售价应定为多少元？

(3)、设商场销售这种商品每天获利w（元），当每件商品的售价定为多少元时，每天销售利润最大？最大利润是多少？

查看试题解析
30. 2022年冬奥会即将在北京召开，某网络经销商购进了一批以冬奥会为主题的文化衫进行销售，文化衫的进价为每件30元，当销售单价定为70元时，每天可售出20件，每销售一件需缴纳网络平台管理费2元，为了扩大销售，增加盈利，决定采取适当的降价措施，经调查发现：销售单价每降低1元，则每天可多售出2件（销售单价不低于进价），若设这款文化衫的销售单价为x（元），每天的销售量为y（件）．

(1)、求每天的销售量y（件）与销售单价x（元）之间的函数关系式；

(2)、当销售单价为多少元时，销售这款文化衫每天所获得的利润最大，最大利润为多少元？

查看试题解析
31. 小美打算买一束百合和康乃馨组合的鲜花，在“母亲节”祝福妈妈.已知买2支百合和1支康乃馨共需花费14元，3支康乃馨的价格比2支百合的价格多2元.

(1)、求买一支康乃馨和一支百合各需多少元？

(2)、小美准备买康乃馨和百合共11支，且百合不少于2支.设买这束鲜花所需费用为w元，康乃馨有x支，求w与x之间的函数关系式，并设计一种使费用最少的买花方案，写出最少费用.

查看试题解析
32. 某超市销售一种商品，每件成本为50元，销售人员经调查发现，销售单价为100元时，每月的销售量为50件，而销售单价每降低2元，则每月可多售出10件，且要求销售单价不得低于成本．

(1)、求该商品每月的销售量y（件）与销售单价x（元）之间的函数关系式；（不需要求自变量取值范围）

(2)、若使该商品每月的销售利润为4000元，并使顾客获得更多的实惠，销售单价应定为多少元？

(3)、超市的销售人员发现：当该商品每月销售量超过某一数量时，会出现所获利润反而减小的情况，为了每月所获利润最大，该商品销售单价应定为多少元？

查看试题解析
33. 渠县是全国优质黄花主产地，某加工厂加工黄花的成本为30元/千克，根据市场调查发现，批发价定为48元/千克时，每天可销售500千克.为增大市场占有率，在保证盈利的情况下，工厂采取降价措施.批发价每千克降低1元，每天销量可增加50千克.

(1)、写出工厂每天的利润 $W$ 元与降价 $x$ 元之间的函数关系.当降价2元时，工厂每天的利润为多少元？

(2)、当降价多少元时，工厂每天的利润最大，最大为多少元？

(3)、若工厂每天的利润要达到9750元，并让利于民，则定价应为多少元？

查看试题解析

34. 某超市从厂家购进A、B两种型号的水杯，两次购进水杯的情况如下表：

进货批次	A型水杯（个）	B型水杯（个）	总费用（元）
一	100	200	8000
二	200	300	13000

(1)、求A、B两种型号的水杯进价各是多少元？

(2)、在销售过程中，A型水杯因为物美价廉而更受消费者喜欢.为了增大B型水杯的销售量，超市决定对B型水杯进行降价销售，当销售价为44元时，每天可以售出20个，每降价1元，每天将多售出5个，请问超市应将B型水杯降价多少元时，每天售出B型水杯的利润达到最大？最大利润是多少？

(3)、第三次进货用10000元钱购进这两种水杯，如果每销售出一个A型水杯可获利10元，售出一个B型水杯可获利9元，超市决定每售出一个A型水杯就为当地“新冠疫情防控”捐b元用于购买防控物资.若A、B两种型号的水杯在全部售出的情况下，捐款后所得的利润始终不变，此时b为多少？利润为多少？

查看试题解析

35. 某商贸公司购进某种商品的成本为20元/ $kg$ ，经过市场调研发现，这种商品在未来40天的销售单价y（元/ $kg$ ）与时间x（天）之间的函数关系式为： $y = {\begin{array}{l} 0.25 x + 30 (1 \leq x \leq 20) \\ 35 (20 < x \leq 40) \end{array}$ 且x为整数，且日销量 $m (kg)$ 与时间x（天）之间的变化规律符合一次函数关系，如下表：

时间x（天）

1

3

6

10

…

日销量 $m (kg)$

142

138

132

124

…

填空：

(1)、m与x的函数关系为；

(2)、哪一天的销售利润最大？最大日销售利润是多少？

(3)、在实际销售的前20天中，公司决定每销售 $1kg$ 商品就捐赠n元利润（ $n < 4$ ）给当地福利院，后发现：在前20天中，每天扣除捐赠后的日销售利润随时间x的增大而增大，求n的取值范围.

查看试题解析
36. 在“乡村振兴”行动中，某村办企业以 $A$ ， $B$ 两种农作物为原料开发了一种有机产品， $A$ 原料的单价是 $B$ 原料单价的1.5倍，若用900元收购 $A$ 原料会比用900元收购 $B$ 原料少 $100 kg$ .生产该产品每盒需要 $A$ 原料 $2 kg$ 和 $B$ 原料 $4 kg$ ，每盒还需其他成本9元.市场调查发现：该产品每盒的售价是60元时，每天可以销售500盒；每涨价1元，每天少销售10盒.

(1)、求每盒产品的成本（成本＝原料费＋其他成本）；

(2)、设每盒产品的售价是 $x$ 元（ $x$ 是整数），每天的利润是 $w$ 元，求 $w$ 关于 $x$ 的函数解析式（不需要写出自变量的取值范围）；

(3)、若每盒产品的售价不超过 $a$ 元（ $a$ 是大于60的常数，且是整数），直接写出每天的最大利润.

查看试题解析
37. 红星公司销售一种成本为40元/件的产品，若月销售单价不高于50元/件.一个月可售出5万件；月销售单价每涨价1元，月销售量就减少 $0.1$ 万件.其中月销售单价不低于成本.设月销售单价为x（单位：元/件），月销售量为y（单位：万件）.

(1)、直接写出y与x之间的函数关系式，并写出自变量x的取值范围；

(2)、当月销售单价是多少元/件时，月销售利润最大，最大利润是多少万元？

(3)、为响应国家“乡村振兴”政策，该公司决定在某月每销售1件产品便向大别山区捐款a元.已知该公司捐款当月的月销售单价不高于70元/件，月销售最大利润是78万元，求a的值.

查看试题解析
38. 超市购进某种苹果，如果进价增加2元/千克要用300元；如果进价减少2元/千克，同样数量的苹果只用200元.

(1)、求苹果的进价.

(2)、如果购进这种苹果不超过100千克，就按原价购进；如果购进苹果超过100千克，超过部分购进价格减少2元/千克.写出购进苹果的支出y（元）与购进数量x（千克）之间的函数关系式.

(3)、超市一天购进苹果数量不超过300千克，且购进苹果当天全部销售完.据统计，销售单价z（元/千克）与一天销售数量x（千克）的关系为 $z = - \frac{1}{100} x + 12$ .在（2）的条件下，要使超市销售苹果利润w（元）最大，求一天购进苹果数量.（利润＝销售收入 $-$ 购进支出）

查看试题解析
39. 鄂尔多斯市某宾馆共有50个房间供游客居住，每间房价不低于200元且不超过320元、如果游客居住房间，宾馆需对每个房间每天支出20元的各种费用．已知每个房间定价x（元）和游客居住房间数y（间）符合一次函数关系，如图是y关于x的函数图象．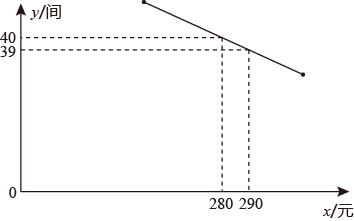

(1)、求y与x之间的函数解析式，并写出自变量x的取值范围；

(2)、当房价定为多少元时，宾馆利润最大？最大利润是多少元？

查看试题解析
40. 某电商销售某种商品一段时间后，发现该商品每天的销售量y（单位：千克）和每千克的售价x（单位：元）满足一次函数关系（如图所示），其中 $50 \leq x \leq 80$ ，

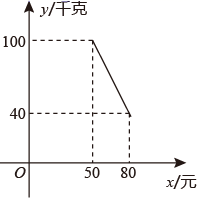(1)、求y关于x的函数解析式；

(2)、若该种商品的成本为每千克40元，该电商如何定价才能使每天获得的利润最大？最大利润是多少？

查看试题解析

销售单价x（元/件）	…	35	40	45	…
每天销售数量y（件）	…	90	80	70	…

销售单价x（元/千克）	…	20	22.5	25	37.5	40	…
销售量y（千克）	…	30	27.5	25	12.5	10	…

	A型	B型
车床数量/台	▲	$x$
每台车床获利/万元	10	▲

x	40	70	90
y	180	90	30
W	3600	4500	2100

x	…	4.0	5.0	5.5	6.5	7.5	…
y	…	8.0	6.0	5.0	3.0	1.0	…

$x$	4	5	6	7	8
$y_{1}$	0	0.5	1	1.5	2

时间x（天）	1	3	6	10	…
日销量 $m (kg)$	142	138	132	124	…