第二十七章 相似 章末测试 人教版九年级下册同步练习
试卷更新日期:2022-12-29 类型:单元试卷
一、单选题
-
1. 如图: , , 那么CE的长为( )
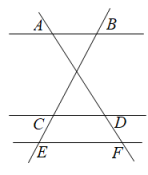 A、3 B、4 C、5 D、62. 已知 , 如果 , , 那么与的周长比为( )A、3:2 B、3:4 C、2:5 D、5:23. 一般认为,如果一个人的肚脐以上的高度与肚脐以下的高度符合黄金分割,则这个人身材好.如图,是一个参加空姐选拔的选手的实际身高情况,如果要使身材好,那么她穿鞋子的高度最好为( ) . (精确到 , 参考数据:黄金分割比为)
A、3 B、4 C、5 D、62. 已知 , 如果 , , 那么与的周长比为( )A、3:2 B、3:4 C、2:5 D、5:23. 一般认为,如果一个人的肚脐以上的高度与肚脐以下的高度符合黄金分割,则这个人身材好.如图,是一个参加空姐选拔的选手的实际身高情况,如果要使身材好,那么她穿鞋子的高度最好为( ) . (精确到 , 参考数据:黄金分割比为)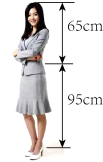 A、5 B、8 C、10 D、124. 如图,如果 , 那么添加下列一个条件后,仍不能确定的是( )
A、5 B、8 C、10 D、124. 如图,如果 , 那么添加下列一个条件后,仍不能确定的是( ) A、 B、 C、 D、5. 如图,在中,分别为线段的中点,设的面积为的面积为 , 则=( )
A、 B、 C、 D、5. 如图,在中,分别为线段的中点,设的面积为的面积为 , 则=( ) A、 B、 C、 D、6. 如图,把△ABC沿AB边平移到△DEF的位置,它们重叠部分的面积是△ABC面积的一半,若AB= , 则此三角形移动的距离是( )
A、 B、 C、 D、6. 如图,把△ABC沿AB边平移到△DEF的位置,它们重叠部分的面积是△ABC面积的一半,若AB= , 则此三角形移动的距离是( ) A、-1 B、 C、1 D、7. 如图,正方形的边在的边上,顶点D、G分别在边 上,已知的边长15厘米,高为10厘米,则正方形的边长是( )
A、-1 B、 C、1 D、7. 如图,正方形的边在的边上,顶点D、G分别在边 上,已知的边长15厘米,高为10厘米,则正方形的边长是( ) A、4厘米 B、5厘米 C、6厘米 D、8厘米8. 如图,小亮的数学兴趣小组利用标杆BE测量学校旗杆CD的高度,标杆BE高1.m,测得AB=2m,BC=14m,则旗杆CD高度是( )
A、4厘米 B、5厘米 C、6厘米 D、8厘米8. 如图,小亮的数学兴趣小组利用标杆BE测量学校旗杆CD的高度,标杆BE高1.m,测得AB=2m,BC=14m,则旗杆CD高度是( ) A、9m B、10.m C、12m D、16m9. 如图,以点为位似中心,把放大2倍得到 . 下列说法错误的是( )
A、9m B、10.m C、12m D、16m9. 如图,以点为位似中心,把放大2倍得到 . 下列说法错误的是( )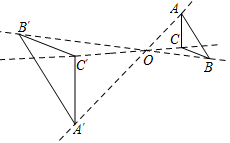 A、 B、 C、 D、直线经过点10. 如图,已知菱形的边长为4,E是的中点,平分交于点F , 交于点G , 若 , 则的长是( )
A、 B、 C、 D、直线经过点10. 如图,已知菱形的边长为4,E是的中点,平分交于点F , 交于点G , 若 , 则的长是( )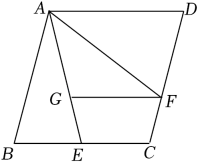 A、3 B、 C、 D、
A、3 B、 C、 D、二、填空题
-
11. 四边形ABCD和四边形A'B'C'D'是相似图形,点A,B,C,D分别与点A',B',C',D'对应,已知BC=3,CD=2.4,B'C'=2,那么C'D'的长是.12. 如图,在四边形中 , 添加一个条件 , 可以利用定理“斜边和直角边对应成比例,两个直角三角形相似”证明 .
 13. 如图,在中, , , , 点是边上的一点,过点作 , 交于点 , 作的平分线交于点 , 连接.若的面积是2,则的值是.
13. 如图,在中, , , , 点是边上的一点,过点作 , 交于点 , 作的平分线交于点 , 连接.若的面积是2,则的值是.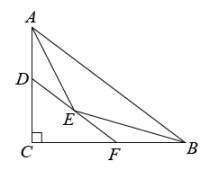 14. 如图,已知点D为中边的中点, , 直线交于点G,交的延长线于点F,若 , , 则的长为 .
14. 如图,已知点D为中边的中点, , 直线交于点G,交的延长线于点F,若 , , 则的长为 . 15. 如图,数学兴趣小组利用硬纸板自制的Rt△ABC来测量操场旗杆MN的高度,他们通过调整测量位置,并使边AC与旗杆顶点M在同一直线上,且Rt△ABC与△AEM在同一个平面内.已知AC=0.8米,BC=0.5米,目测点A到地面的距离AD=1.5米,到旗杆的水平距离AE=20米,则旗杆MN的高度为 米.
15. 如图,数学兴趣小组利用硬纸板自制的Rt△ABC来测量操场旗杆MN的高度,他们通过调整测量位置,并使边AC与旗杆顶点M在同一直线上,且Rt△ABC与△AEM在同一个平面内.已知AC=0.8米,BC=0.5米,目测点A到地面的距离AD=1.5米,到旗杆的水平距离AE=20米,则旗杆MN的高度为 米. 16. 如图,将▱ABCD绕点A逆时针旋转到▱AB′C′D′的位置,使点B′落在BC上,B′C′与CD交于点E.若AB=3,BC=4,BB′=1,则CE的长为 .
16. 如图,将▱ABCD绕点A逆时针旋转到▱AB′C′D′的位置,使点B′落在BC上,B′C′与CD交于点E.若AB=3,BC=4,BB′=1,则CE的长为 .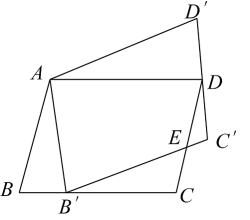
三、作图题
-
17. 如图,在边长为个单位长度的小正方形网格中,

( 1 )画出向上平移6个单位,再向右平移5个单位后的;
( 2 )以点B为位似中心,将放大为原来的2倍,得到 , 请在网格中画出;
( 3 )直接写出的面积,及 , 的坐标.
四、解答题
-
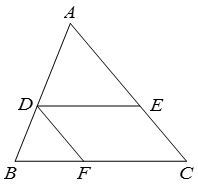
18. 如图,在△ABC中,DE∥BC,DF∥AC.求证:△ADE∽△DBF.
 19. 如图,在中, , D,E分别为边上的点, , 当时,求的长.
19. 如图,在中, , D,E分别为边上的点, , 当时,求的长.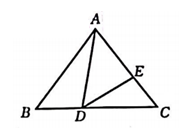 20. 在四边形ABCD中,对角线AC、BD交于点O,若四边形ABCD是正方形,如图1:则有AC=BD,AC⊥BD.
20. 在四边形ABCD中,对角线AC、BD交于点O,若四边形ABCD是正方形,如图1:则有AC=BD,AC⊥BD.
旋转图1中的Rt△COD到图2所示的位置,AC’与BD’有什么关系?(直接写出);
若四边形ABCD是菱形,∠ABC=60°,旋转Rt△COD至图3所示的位置,AC’与BD’又有什么关系?写出结论并证明.
五、综合题
-
21. 在四边形ABCD中, ADC=∠ACB,AC为对角线,AD·CB=DC·AC.
 (1)、如图1,求证:AC平分∠DAB;(2)、如图1,若AC=8,AB=12,求AD的长;(3)、如图2,若∠ADC=∠ACB=90°,E为AB的中点,连接CE、DE,DE与AC交于点F,CB=6,CE=5,求的值.
(1)、如图1,求证:AC平分∠DAB;(2)、如图1,若AC=8,AB=12,求AD的长;(3)、如图2,若∠ADC=∠ACB=90°,E为AB的中点,连接CE、DE,DE与AC交于点F,CB=6,CE=5,求的值.
-