27.2.3 相似三角形的应用举例 人教版九年级下册同步练习
试卷更新日期：2022-12-29 类型：同步测试
一、单选题
-
1. 高4米的旗杆在水平地面上的影长为6米，此时测得附近一个建筑物的影长24米，则该建筑物的高度为（ ）A、10米 B、16米 C、26米 D、36米2. 如图，阳光从教室的窗户射入室内，窗户框AB在地面上的影子长DE＝1.8m，窗户下沿到地面的距离BC＝1m，EC＝1.2m，那么窗户的高AB为（ ）
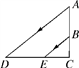A、1.5m B、1.6m C、1.86m D、2.16m3. 如图所示，某校数学兴趣小组利用标杆BE测量物的高度，已知标杆BE高1.5m，测得AB＝1.2m，AC＝14m，则建筑物CD的高是（ ）
A、17.5m B、17m C、16.5m D、18m4. 如图，小明在A时测得某树的影长为 ， B时又测得该树的影长为 ， 若两次日照的光线互相垂直，则树的高度为（ ）
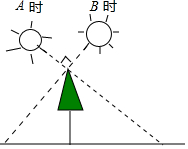A、 B、 C、 D、5. 如图，某次课外实践活动中，小红在地面点B处利用标杆FC测量一旗杆ED的高度．小红眼睛点A与标杆顶端点F，旗杆顶端点E在同一直线上，点B，C，D也在同一条直线上．已知小红眼睛到地面距离米，标杆高米，且米，米，则旗杆ED的高度为（ ）
A、15.4米 B、17米 C、17.6米 D、19.2米6. 如图，A，B两地被池塘隔开，小明通过下列方法测出了A、B间的距离：先在外选一点C，在、上分别找点M，N，使得 ， ， 测量出的长为 ， 由此可知A、B间的距离为（ ）
A、 B、 C、 D、二、填空题
-
7. 据《墨经》记载，在两千多年前，我国学者墨子和他的学生做了“小孔成像”实验，阐释了光的直线传播原理．小孔成像的示意图如图所示，光线经过小孔O，物体AB在幕布上形成倒立的实像CD（点A，B的对应点分别是C，D）．若物体AB的高为6cm，实像CD的高度为3cm，则小孔O到BC的距离OE为 ．
8. 如图，为了测量旗杆的高度，某综合实践小组设计了以下方案：用2.5m长的竹竿做测量工具，移动竹竿，保持竹竿与旗杆平行，使竹竿、旗杆的顶端的影子恰好落在地面的同一点．此时，竹竿与这一点相距5m、与旗杆相距20m，则旗杆的高度为m．
9. 为了测量河宽AB，有如下方法：如图，取一根标尺CD横放，使CD∥AB，并使点B，D，O和点A，C，O分别在同一条直线上，量得CD＝15米，OC＝10米，AC＝20米，则河宽AB的长度为米.
10. 如图是一位同学用激光笔测量某古城墙高度的示意图.点P处放一水平的平面镜，光线从点A出发经平面镜反射后刚好到古城墙的顶端C处，若 ， ， 测得 ， ， ， 则该古城墙的高度是.
11. 如图，小红同学正在使用手电筒进行物理光学实验，地面上从左往右依次是墙、木板和平面镜．手电筒的灯泡在点G处，手电筒的光从平面镜上点B处反射后，恰好经过木板的边缘点F，落在墙上的点E处．点E到地面的高度 ， 点F到地面的高度 ， 灯泡到木板的水平距离 ， 墙到木板的水平距离为 ． 已知 ， 图中点A，B，C，D在同一水平面上．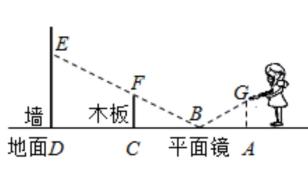
(1)、的长为(2)、灯泡到地面的高度为三、作图题
-
12. 已知：如图，AB和DE是直立在地面上的两根立柱，AB＝5m，某一时刻，AB在阳光下的投影BC＝4m.
(1)、请你在图中画出此时DE在阳光下的投影；(2)、在测量AB的投影长时，同时测出DE在阳光下的投影长为6m，请你计算DE的长.四、解答题
-
13. 如图，是小凯为估算鱼塘的宽AB设计的，在陆地上取点 ， 使得在同一条直线上，在同一条直线上，测得 ． 小凯测得的长为10米，求鱼塘的宽的长是多少米？
-
