2022年全国中考数学真题分类汇编11 反比例函数综合(1)
试卷更新日期:2022-12-29 类型:二轮复习
一、单选题
-
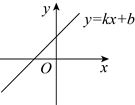
1. 已知一次函数 的图象如图所示,则 与 的图象为( )
 A、
A、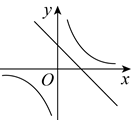 B、
B、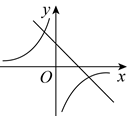 C、
C、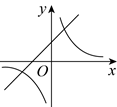 D、
D、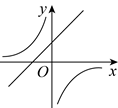 2. 若反比例函数的图象经过点 , 则它的图象也一定经过的点是( )A、 B、 C、 D、3. 如图,在平面直角坐标系中,点O为坐标原点,平行四边形OBAD的顶点B在反比例函数的图象上,顶点A在反比例函数的图象上,顶点D在x轴的负半轴上.若平行四边形OBAD的面积是5,则k的值是( )
2. 若反比例函数的图象经过点 , 则它的图象也一定经过的点是( )A、 B、 C、 D、3. 如图,在平面直角坐标系中,点O为坐标原点,平行四边形OBAD的顶点B在反比例函数的图象上,顶点A在反比例函数的图象上,顶点D在x轴的负半轴上.若平行四边形OBAD的面积是5,则k的值是( )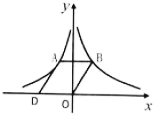 A、2 B、1 C、 D、4. 点 , , , 在反比例函数 图象上,则 , , , 中最小的是( )A、 B、 C、 D、5. 如图,正方形 的顶点分别在反比例函数 和 的图象上.若 轴,点 的横坐标为3,则 ( )
A、2 B、1 C、 D、4. 点 , , , 在反比例函数 图象上,则 , , , 中最小的是( )A、 B、 C、 D、5. 如图,正方形 的顶点分别在反比例函数 和 的图象上.若 轴,点 的横坐标为3,则 ( )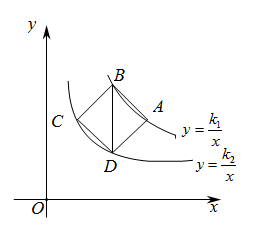 A、36 B、18 C、12 D、96. 如图是同一直角坐标系中函数 和 的图象.观察图象可得不等式 的解集为( )
A、36 B、18 C、12 D、96. 如图是同一直角坐标系中函数 和 的图象.观察图象可得不等式 的解集为( ) A、 B、 或 C、 或 D、 或7. 某项工作,已知每人每天完成的工作量相同,且一个人完成需12天.若m个人共同完成需n天,选取6组数对 ,在坐标系中进行描点,则正确的是()A、
A、 B、 或 C、 或 D、 或7. 某项工作,已知每人每天完成的工作量相同,且一个人完成需12天.若m个人共同完成需n天,选取6组数对 ,在坐标系中进行描点,则正确的是()A、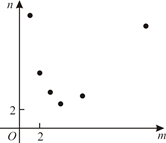 B、
B、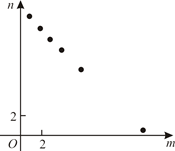 C、
C、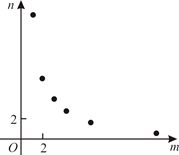 D、
D、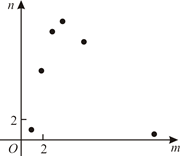 8. 已知经过闭合电路的电流 (单位: )与电路的电阻 (单位: )是反比例函数关系.根据下表判断 和 的大小关系为( )
8. 已知经过闭合电路的电流 (单位: )与电路的电阻 (单位: )是反比例函数关系.根据下表判断 和 的大小关系为( )5
…
…
…
…
…
1
20
30
40
50
60
70
80
90
100
A、 B、 C、 D、9. 已知点 , 在反比例函数的图象上,且 , 则下列结论一定正确的是( )A、 B、 C、 D、10. 在平面直角坐标系中,为坐标原点,已知点、(且),过点、的直线与两坐标轴相交于、两点,连接、 , 则下列结论中成立的是( )①点、在反比例函数的图象上;②成等腰直角三角形;③;④的值随的增大而增大.
A、②③④ B、①③④ C、①②④ D、①②③11. 若点都在反比例函数的图像上,则的大小关系是( )A、 B、 C、 D、12. 某市举行中学生党史知识竞赛,如图用四个点分别描述甲、乙、丙、丁四所学校竞赛成绩的优秀率(该校优秀人数与该校参加竞赛人数的比值)与该校参加竞赛人数的情况,其中描述乙、丁两所学校情况的点恰好在同一个反比例函数的图象上,则这四所学校在这次党史知识竞赛中成绩优秀人数最多的是( ) A、甲 B、乙 C、丙 D、丁13. 如图是反比例函数y=的图象,点A(x,y)是反比例函数图象上任意一点,过点A作AB⊥x轴于点B,连接OA,则△AOB的面积是( )
A、甲 B、乙 C、丙 D、丁13. 如图是反比例函数y=的图象,点A(x,y)是反比例函数图象上任意一点,过点A作AB⊥x轴于点B,连接OA,则△AOB的面积是( )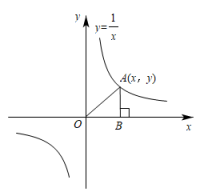 A、1 B、 C、2 D、
A、1 B、 C、2 D、二、填空题
-
14. 如图,在平面直角坐标系中,一次函数 的图象与反比例函数 的图象交于点 .当 时,x的取值范围是.
 15. 如图,已知直线y=2x与双曲线(k为大于零的常数,且x>0)交于点A,若OA= , 则k的值为 .
15. 如图,已知直线y=2x与双曲线(k为大于零的常数,且x>0)交于点A,若OA= , 则k的值为 .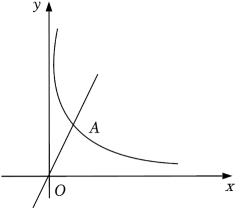 16. 如图,在平面直角坐标系中,正方形的顶点A,B分别在x轴、y轴上,对角线交于点E,反比例函数的图象经过点C,E.若点 , 则k的值是.
16. 如图,在平面直角坐标系中,正方形的顶点A,B分别在x轴、y轴上,对角线交于点E,反比例函数的图象经过点C,E.若点 , 则k的值是. 17. 已知反比例函数的图象分别位于第二、第四象限,则实数k的值可以是.(只需写出一个符合条件的实数)18. 如图,在平面直角坐标系中,等腰直角三角形的斜边轴于点 , 直角顶点在轴上,双曲线经过边的中点 , 若 , 则.
17. 已知反比例函数的图象分别位于第二、第四象限,则实数k的值可以是.(只需写出一个符合条件的实数)18. 如图,在平面直角坐标系中,等腰直角三角形的斜边轴于点 , 直角顶点在轴上,双曲线经过边的中点 , 若 , 则. 19. 正方形ABCD在平面直角坐标系中的位置如图所示,点A的坐标为(2,0),点B的坐标为(0,4).若反比例函数y=(k≠0)的图象经过点C,则k的值为 .
19. 正方形ABCD在平面直角坐标系中的位置如图所示,点A的坐标为(2,0),点B的坐标为(0,4).若反比例函数y=(k≠0)的图象经过点C,则k的值为 . 20. 如图,点A是反比例函数图象上一点,过点A作AB⊥y轴于点D,且点D为线段AB的中点.若点C为x轴上任意一点,且△ABC的面积为4,则k= .
20. 如图,点A是反比例函数图象上一点,过点A作AB⊥y轴于点D,且点D为线段AB的中点.若点C为x轴上任意一点,且△ABC的面积为4,则k= .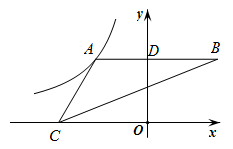 21. 如图,是边长为10的等边三角形,反比例函数的图象与边、分别交于点A、B(点不与点重合若).于点 , 则的值为.
21. 如图,是边长为10的等边三角形,反比例函数的图象与边、分别交于点A、B(点不与点重合若).于点 , 则的值为.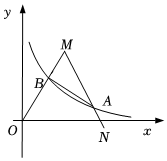 22. 根据物理学知识,在压力不变的情况下,某物体承受的压强是它的受力面积的反比例函数,其函数图象如图所示,当时,该物体承受的压强p的值为 Pa.
22. 根据物理学知识,在压力不变的情况下,某物体承受的压强是它的受力面积的反比例函数,其函数图象如图所示,当时,该物体承受的压强p的值为 Pa. 23. 如图,在平面直角坐标系中,直线与x轴,y轴分别交于点A,B,与反比例函数的图象在第一象限交于点C,若 , 则k的值为.
23. 如图,在平面直角坐标系中,直线与x轴,y轴分别交于点A,B,与反比例函数的图象在第一象限交于点C,若 , 则k的值为. 24. 如图,已知在平面直角坐标系中,点A在x轴负半轴上,点B在第二象限内,反比例函数的图象经过△OAB的顶点B和边AB的中点C,如果△OAB的面积为6,那么k的值是 .
24. 如图,已知在平面直角坐标系中,点A在x轴负半轴上,点B在第二象限内,反比例函数的图象经过△OAB的顶点B和边AB的中点C,如果△OAB的面积为6,那么k的值是 . 25. 已知点A在反比例函数的图象上,点B在x轴正半轴上,若为等腰三角形,且腰长为5,则的长为 .
25. 已知点A在反比例函数的图象上,点B在x轴正半轴上,若为等腰三角形,且腰长为5,则的长为 . 26. 已知点 M(1,2)在反比例函数的图象上,则 k=.27. 如图所示,矩形顶点、在轴上,顶点在第一象限,轴为该矩形的一条对称轴,且矩形的面积为6.若反比例函数的图象经过点 , 则的值为.
26. 已知点 M(1,2)在反比例函数的图象上,则 k=.27. 如图所示,矩形顶点、在轴上,顶点在第一象限,轴为该矩形的一条对称轴,且矩形的面积为6.若反比例函数的图象经过点 , 则的值为.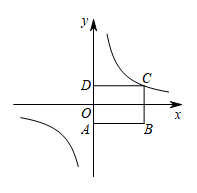 28. 已知点A(−2,m)在一个反比例函数的图象上,点A′与点A关于y轴对称.若点A′在正比例函数的图象上,则这个反比例函数的表达式为.
28. 已知点A(−2,m)在一个反比例函数的图象上,点A′与点A关于y轴对称.若点A′在正比例函数的图象上,则这个反比例函数的表达式为.三、综合题
-
29. 如图,反比例函数与正比例函数的图象交于点和点 , 点是点关于轴的对称点,连接 , .
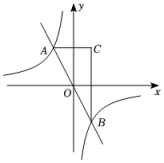 (1)、求该反比例函数的解析式;(2)、求的面积;(3)、请结合函数图象,直接写出不等式的解集.30. 在平面直角坐标系中,已知一次函数与坐标轴分别交于 , 两点,且与反比例函数的图象在第一象限内交于P,K两点,连接 , 的面积为 .
(1)、求该反比例函数的解析式;(2)、求的面积;(3)、请结合函数图象,直接写出不等式的解集.30. 在平面直角坐标系中,已知一次函数与坐标轴分别交于 , 两点,且与反比例函数的图象在第一象限内交于P,K两点,连接 , 的面积为 .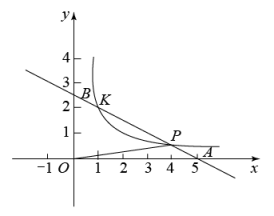 (1)、求一次函数与反比例函数的解析式;(2)、当时,求x的取值范围;(3)、若C为线段上的一个动点,当最小时,求的面积.31. 如图,反比例函数 的图象经过点 和点 ,点 在点 的下方, 平分 ,交 轴于点 .
(1)、求一次函数与反比例函数的解析式;(2)、当时,求x的取值范围;(3)、若C为线段上的一个动点,当最小时,求的面积.31. 如图,反比例函数 的图象经过点 和点 ,点 在点 的下方, 平分 ,交 轴于点 .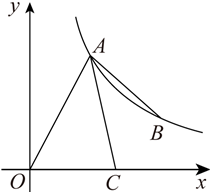 (1)、求反比例函数的表达式.(2)、请用无刻度的直尺和圆规作出线段 的垂直平分线.(要求:不写作法,保留作图痕迹,使用2B铅笔作图)(3)、线段 与(2)中所作的垂直平分线相交于点 ,连接 .求证: .32. 如图,一次函数的图象与轴交于点 , 与轴交于点 , 与反比例函数的图象交于点、若 , .
(1)、求反比例函数的表达式.(2)、请用无刻度的直尺和圆规作出线段 的垂直平分线.(要求:不写作法,保留作图痕迹,使用2B铅笔作图)(3)、线段 与(2)中所作的垂直平分线相交于点 ,连接 .求证: .32. 如图,一次函数的图象与轴交于点 , 与轴交于点 , 与反比例函数的图象交于点、若 , .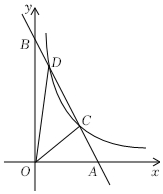 (1)、求一次函数和反比例函数的表达式;(2)、求的面积.33. 如图,直线与反比例函数的图象相交于点 , , 已知点的纵坐标为6
(1)、求一次函数和反比例函数的表达式;(2)、求的面积.33. 如图,直线与反比例函数的图象相交于点 , , 已知点的纵坐标为6 (1)、求的值;(2)、若点是轴上一点,且的面积为3,求点的坐标.34. 如图,已知一次函数的图象与函数的图象交于 , 两点,与轴交于点将直线沿轴向上平移个单位长度得到直线 , 与轴交于点.
(1)、求的值;(2)、若点是轴上一点,且的面积为3,求点的坐标.34. 如图,已知一次函数的图象与函数的图象交于 , 两点,与轴交于点将直线沿轴向上平移个单位长度得到直线 , 与轴交于点. (1)、求与的解析式;(2)、观察图象,直接写出时的取值范围;(3)、连接 , , 若的面积为6,则的值为.35. 如图,一次函数 的图象与反比例函数 的图象交于点 ,与y轴交于点B,与x轴交于点 .
(1)、求与的解析式;(2)、观察图象,直接写出时的取值范围;(3)、连接 , , 若的面积为6,则的值为.35. 如图,一次函数 的图象与反比例函数 的图象交于点 ,与y轴交于点B,与x轴交于点 .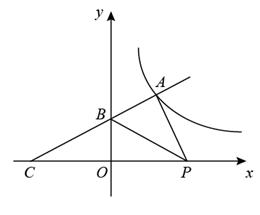 (1)、求k与m的值;(2)、 为x轴上的一动点,当△APB的面积为 时,求a的值.36. 如图,在平面直角坐标系xOy中,函数y=x+b的图象与函数(x>0)的图象相交于点B(1,6),并与x轴交于点A.点C是线段AB上一点,△OAC与△OAB的面积比为2:3
(1)、求k与m的值;(2)、 为x轴上的一动点,当△APB的面积为 时,求a的值.36. 如图,在平面直角坐标系xOy中,函数y=x+b的图象与函数(x>0)的图象相交于点B(1,6),并与x轴交于点A.点C是线段AB上一点,△OAC与△OAB的面积比为2:3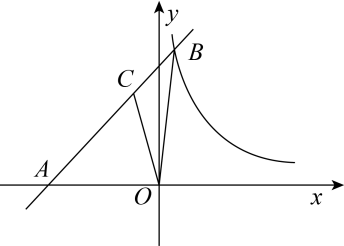 (1)、求k和b的值;(2)、若将△OAC绕点O顺时针旋转,使点C的对应点C′落在x轴正半轴上,得到△OA′C′,判断点A′是否在函数(x>0)的图象上,并说明理由.37. 如图,已知正比例函数与反比例函数的图象交于 , 两点.
(1)、求k和b的值;(2)、若将△OAC绕点O顺时针旋转,使点C的对应点C′落在x轴正半轴上,得到△OA′C′,判断点A′是否在函数(x>0)的图象上,并说明理由.37. 如图,已知正比例函数与反比例函数的图象交于 , 两点.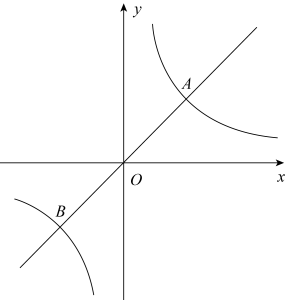 (1)、求的解析式并直接写出时的取值范围;(2)、以为一条对角线作菱形,它的周长为 , 在此菱形的四条边中任选一条,求其所在直线的解析式.38. 如图,点在反比例函数的图象上,点B在y轴上, , 将线段向右下方平移,得到线段 , 此时点C落在反比例函数的图象上,点D落在x轴正半轴上,且 .
(1)、求的解析式并直接写出时的取值范围;(2)、以为一条对角线作菱形,它的周长为 , 在此菱形的四条边中任选一条,求其所在直线的解析式.38. 如图,点在反比例函数的图象上,点B在y轴上, , 将线段向右下方平移,得到线段 , 此时点C落在反比例函数的图象上,点D落在x轴正半轴上,且 .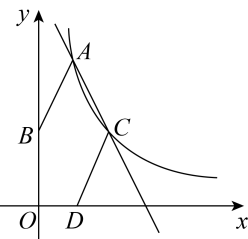 (1)、点B的坐标为 , 点D的坐标为 , 点C的坐标为(用含m的式子表示);(2)、求k的值和直线的表达式.
(1)、点B的坐标为 , 点D的坐标为 , 点C的坐标为(用含m的式子表示);(2)、求k的值和直线的表达式.