2022年全国中考数学真题分类汇编10 反比例函数图像及性质
试卷更新日期:2022-12-29 类型:二轮复习
一、单选题
-
1. 如图,正比例函数与反比例函数的图象交于、B两点,当时,x的取值范围是( )
 A、或 B、或 C、或 D、或2. 在同一平面直角坐标系中,函数y=ax+b与(其中a,b是常数,ab≠0)的大致图象是( )A、
A、或 B、或 C、或 D、或2. 在同一平面直角坐标系中,函数y=ax+b与(其中a,b是常数,ab≠0)的大致图象是( )A、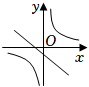 B、
B、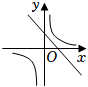 C、
C、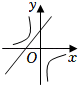 D、
D、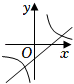 3. 若点A(-2,y1),B(-1,y2)都在反比例函数y=的图象上,则y1 , y2的大小关系是( )A、y1<y2 B、y1=y2 C、y1>y2 D、不能确定4. 二次函数y=ax2+bx+c的图象如图所示,则一次函数y=bx+c和反比例函数y=在同一平面直角坐标系中的图象可能是( )
3. 若点A(-2,y1),B(-1,y2)都在反比例函数y=的图象上,则y1 , y2的大小关系是( )A、y1<y2 B、y1=y2 C、y1>y2 D、不能确定4. 二次函数y=ax2+bx+c的图象如图所示,则一次函数y=bx+c和反比例函数y=在同一平面直角坐标系中的图象可能是( ) A、
A、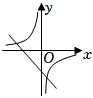 B、
B、 C、
C、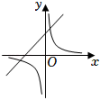 D、
D、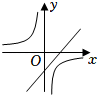 5. 在显示汽车油箱内油量的装置模拟示意图中,电压一定时,油箱中浮子随油面下降而落下,带动滑杆使滑动变阻器滑片向上移动,从而改变电路中的电流,电流表的示数对应油量体积,把电流表刻度改为相应油量体积数,由此知道油箱里剩余油量.在不考虑其他因素的条件下,油箱中油的体积与电路中总电阻是反比例关系,电流与也是反比例关系,则与的函数关系是( )
5. 在显示汽车油箱内油量的装置模拟示意图中,电压一定时,油箱中浮子随油面下降而落下,带动滑杆使滑动变阻器滑片向上移动,从而改变电路中的电流,电流表的示数对应油量体积,把电流表刻度改为相应油量体积数,由此知道油箱里剩余油量.在不考虑其他因素的条件下,油箱中油的体积与电路中总电阻是反比例关系,电流与也是反比例关系,则与的函数关系是( ) A、反比例函数 B、正比例函数 C、二次函数 D、以上答案都不对6. 在平面直角坐标系中,反比例函数的图象如图所示,则一次函数的图象经过的象限是( )
A、反比例函数 B、正比例函数 C、二次函数 D、以上答案都不对6. 在平面直角坐标系中,反比例函数的图象如图所示,则一次函数的图象经过的象限是( ) A、一、二、三 B、一、二、四 C、一、三、四 D、二、三、四7. 已知反比例函数y=(k≠0),且在各自象限内,y随x的增大而增大,则下列点可能在这个函数图象上的为( )A、(2,3) B、(-2,3) C、(3,0) D、(-3,0)8. 地球周围的大气层阻挡了紫外线和宇宙射线对地球生命的伤害,同时产生一定的大气压,海拔不同,大气压不同,观察图中数据,你发现,正确的是( )
A、一、二、三 B、一、二、四 C、一、三、四 D、二、三、四7. 已知反比例函数y=(k≠0),且在各自象限内,y随x的增大而增大,则下列点可能在这个函数图象上的为( )A、(2,3) B、(-2,3) C、(3,0) D、(-3,0)8. 地球周围的大气层阻挡了紫外线和宇宙射线对地球生命的伤害,同时产生一定的大气压,海拔不同,大气压不同,观察图中数据,你发现,正确的是( ) A、海拔越高,大气压越大 B、图中曲线是反比例函数的图象 C、海拔为4千米时,大气压约为70千帕 D、图中曲线表达了大气压和海拔两个量之间的变化关系9. 如图,正比例函数y=ax(a为常数,且a≠0)和反比例函数y=(k为常数,且k≠0)的图象相交于A(﹣2,m)和B两点,则不等式ax>的解集为( )
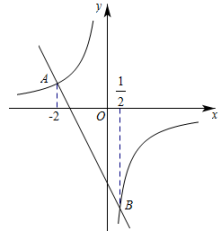
A、海拔越高,大气压越大 B、图中曲线是反比例函数的图象 C、海拔为4千米时,大气压约为70千帕 D、图中曲线表达了大气压和海拔两个量之间的变化关系9. 如图,正比例函数y=ax(a为常数,且a≠0)和反比例函数y=(k为常数,且k≠0)的图象相交于A(﹣2,m)和B两点,则不等式ax>的解集为( )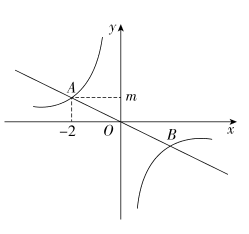 A、x<﹣2或x>2 B、﹣2<x<2 C、﹣2<x<0或x>2 D、x<﹣2或0<x<210. 如图,一次函数与反比例函数的图象相交于A,B两点,点A的横坐标为2,点B的横坐标为 , 则不等式的解集是( )
A、x<﹣2或x>2 B、﹣2<x<2 C、﹣2<x<0或x>2 D、x<﹣2或0<x<210. 如图,一次函数与反比例函数的图象相交于A,B两点,点A的横坐标为2,点B的横坐标为 , 则不等式的解集是( )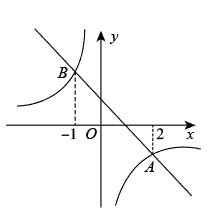 A、或 B、或 C、或 D、11. 如图,在平面直角坐标系中,点M为x轴正半轴上一点,过点M的直线l∥y轴,且直线l分别与反比例函数和的图象交于P、Q两点.若S△POQ=15,则k的值为( )
A、或 B、或 C、或 D、11. 如图,在平面直角坐标系中,点M为x轴正半轴上一点,过点M的直线l∥y轴,且直线l分别与反比例函数和的图象交于P、Q两点.若S△POQ=15,则k的值为( )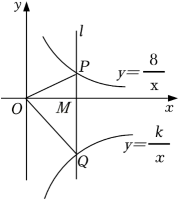 A、38 B、22 C、﹣7 D、﹣2212. 如图,在平面直角坐标系中有 , , , 四个点,其中恰有三点在反比例函数的图象上.根据图中四点的位置,判断这四个点中不在函数的图象上的点是( )
A、38 B、22 C、﹣7 D、﹣2212. 如图,在平面直角坐标系中有 , , , 四个点,其中恰有三点在反比例函数的图象上.根据图中四点的位置,判断这四个点中不在函数的图象上的点是( )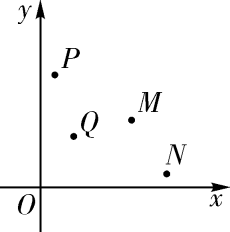 A、点 B、点 C、点 D、点13. 已知点在下列某一函数图象上,且那么这个函数是( )A、 B、 C、 D、14. 一次函数y=mx+n的图象与反比例函数y= 的图象交于点A、B,其中点A、B的坐标为A(- ,-2m)、B(m,1),则△OAB的面积( )A、3 B、 C、 D、
A、点 B、点 C、点 D、点13. 已知点在下列某一函数图象上,且那么这个函数是( )A、 B、 C、 D、14. 一次函数y=mx+n的图象与反比例函数y= 的图象交于点A、B,其中点A、B的坐标为A(- ,-2m)、B(m,1),则△OAB的面积( )A、3 B、 C、 D、二、填空题
-
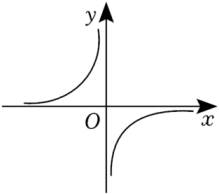
15. 在平面直角坐标系中,将点向下平移5个单位长度得到点 , 若点恰好在反比例函数的图象上,则的值是.16. 将双曲线向右平移2个单位,再向下平移1个单位,得到的新双曲线与直线相交于2022个点,则这2022个点的横坐标之和为 .17. 反比例函数的图象经过、两点,当时, , 写出符合条件的的值(答案不唯一,写出一个即可).18. 反比例函数y=的图像分布情况如图所示,则k的值可以是 (写出一个符合条件的k值即可).
 19. 已知点 , 在反比例函数的图象上,则与的大小关系是 .20. 如图,一块砖的A,B,C三个面的面积之比是5:3:1,如果A,B,C三个面分别向下在地上,地面所受压强分别为 , , , 压强的计算公式为 , 其中P是压强,F是压力,S是受力面积,则 , , 的大小关系为(用小于号连接).
19. 已知点 , 在反比例函数的图象上,则与的大小关系是 .20. 如图,一块砖的A,B,C三个面的面积之比是5:3:1,如果A,B,C三个面分别向下在地上,地面所受压强分别为 , , , 压强的计算公式为 , 其中P是压强,F是压力,S是受力面积,则 , , 的大小关系为(用小于号连接).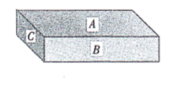 21. 科技小组为了验证某电路的电压U(V)、电流I(A)、电阻 三者之间的关系: ,测得数据如下:
21. 科技小组为了验证某电路的电压U(V)、电流I(A)、电阻 三者之间的关系: ,测得数据如下:100
200
220
400
2.2
1.1
1
0.55
那么,当电阻 时,电流 A.
22. 如图,在平面直角坐标系中,一次函数的图象经过点且与函数的图象交于点.若一次函数随的增大而增大,则的取值范围是.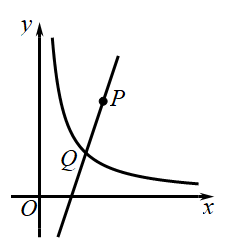 23. 在反比例函数的图象的每一支上,y都随x的增大而减小,且整式是一个完全平方式,则该反比例函数的解析式为.24. 反比例函数与一次函数交于点 , 则k的值为.25. 如图,点A在反比例函数y=的图象上,且点A的横坐标为a(a<0),AB⊥y轴于点B,若AOB的面积是3,则k的值是 .
23. 在反比例函数的图象的每一支上,y都随x的增大而减小,且整式是一个完全平方式,则该反比例函数的解析式为.24. 反比例函数与一次函数交于点 , 则k的值为.25. 如图,点A在反比例函数y=的图象上,且点A的横坐标为a(a<0),AB⊥y轴于点B,若AOB的面积是3,则k的值是 .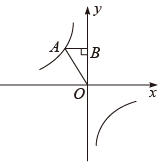 26. 点、在反比例函数的图象上,若 , 则的取值范围是 .27. 已知反比例函数的图象经过点 , 则a的值为 .28. 在平面直角坐标系中,若点在反比例函数的图象上,则(填“>”“=”或“<”)
26. 点、在反比例函数的图象上,若 , 则的取值范围是 .27. 已知反比例函数的图象经过点 , 则a的值为 .28. 在平面直角坐标系中,若点在反比例函数的图象上,则(填“>”“=”或“<”)三、综合题
-
29. 如图,一次函数的图象与反比例函数的图象交于点和点 .
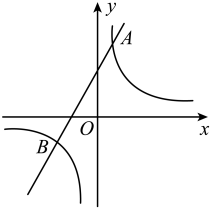 (1)、求一次函数的表达式;(2)、结合图象,写出当时,满足的x的取值范围;(3)、将一次函数的图象平移,使其经过坐标原点.直接写出一个反比例函数表达式,使它的图像与平移后的一次函数图象无交点.30. 如图,正比例函数与反比例函数的图象交于 , 两点.
(1)、求一次函数的表达式;(2)、结合图象,写出当时,满足的x的取值范围;(3)、将一次函数的图象平移,使其经过坐标原点.直接写出一个反比例函数表达式,使它的图像与平移后的一次函数图象无交点.30. 如图,正比例函数与反比例函数的图象交于 , 两点.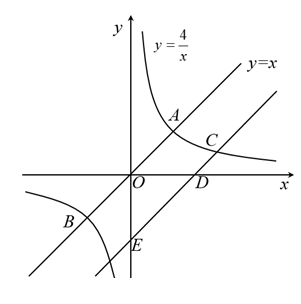 (1)、求 , 两点的坐标;(2)、将直线向下平移个单位长度,与反比例函数在第一象限的图象交于点 , 与轴交于点 , 与轴交于点 , 若 , 求的值.31. 如图,点A在反比例函数 的图象上, 轴,垂足为 ,过 作 轴,交过B点的一次函数 的图象于D点,交反比例函数的图象于E点, .
(1)、求 , 两点的坐标;(2)、将直线向下平移个单位长度,与反比例函数在第一象限的图象交于点 , 与轴交于点 , 与轴交于点 , 若 , 求的值.31. 如图,点A在反比例函数 的图象上, 轴,垂足为 ,过 作 轴,交过B点的一次函数 的图象于D点,交反比例函数的图象于E点, . (1)、求反比例函数 和一次函数 的表达式:(2)、求DE的长.32. 如图,已知一次函数y=ax+b与反比例函数y=(x<0)的图像交于A(﹣2,4),B(﹣4,2)两点,且与x轴和y轴分别交于点C、点D.
(1)、求反比例函数 和一次函数 的表达式:(2)、求DE的长.32. 如图,已知一次函数y=ax+b与反比例函数y=(x<0)的图像交于A(﹣2,4),B(﹣4,2)两点,且与x轴和y轴分别交于点C、点D.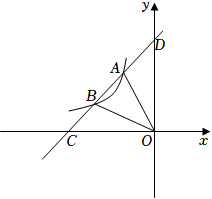 (1)、根据图像直接写出不等式<ax+b的解集;(2)、求反比例函数与一次函数的解析式;(3)、点P在y轴上,且S△AOP=S△AOB , 请求出点P的坐标.33. 某燃气公司计划在地下修建一个容积为V(V为定值,单位:m3)的圆柱形天然气储存室,储存室的底面积S(单位:m2) 与其深度d(单位:m)是反比例函数关系,它的图象如图所示.
(1)、根据图像直接写出不等式<ax+b的解集;(2)、求反比例函数与一次函数的解析式;(3)、点P在y轴上,且S△AOP=S△AOB , 请求出点P的坐标.33. 某燃气公司计划在地下修建一个容积为V(V为定值,单位:m3)的圆柱形天然气储存室,储存室的底面积S(单位:m2) 与其深度d(单位:m)是反比例函数关系,它的图象如图所示.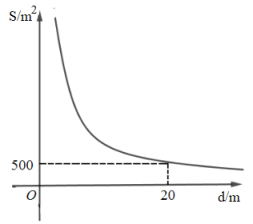 (1)、求储存室的容积V的值;(2)、受地形条件限制,储存室的深度d需要满足16≤d≤25,求储存室的底面积S的取值范围.34. 密闭容器内有一定质量的二氧化碳,当容器的体积V(单位:)变化时,气体的密度(单位:)随之变化.已知密度与体积V是反比例函数关系,它的图象如图所示,当时, .
(1)、求储存室的容积V的值;(2)、受地形条件限制,储存室的深度d需要满足16≤d≤25,求储存室的底面积S的取值范围.34. 密闭容器内有一定质量的二氧化碳,当容器的体积V(单位:)变化时,气体的密度(单位:)随之变化.已知密度与体积V是反比例函数关系,它的图象如图所示,当时, . (1)、求密度关于体积V的函数解析式;(2)、若 , 求二氧化碳密度的变化范围.35. 如图,一次函数y=kx+b(k、b为常数,k≠0)的图象与反比例函数y=(m为常数,m≠0)的图象在第二象限交于点A(﹣4,3),与y轴负半轴交于点B,且OA=OB
(1)、求密度关于体积V的函数解析式;(2)、若 , 求二氧化碳密度的变化范围.35. 如图,一次函数y=kx+b(k、b为常数,k≠0)的图象与反比例函数y=(m为常数,m≠0)的图象在第二象限交于点A(﹣4,3),与y轴负半轴交于点B,且OA=OB (1)、求反比例函数和一次函数的解析式.(2)、根据图象直接写出当x<0时,不等式kx+b≤的解集.36. 一次函数的图象与反比例函数的图象相交于 , 两点.
(1)、求反比例函数和一次函数的解析式.(2)、根据图象直接写出当x<0时,不等式kx+b≤的解集.36. 一次函数的图象与反比例函数的图象相交于 , 两点. (1)、求这个反比例函数的表达式;(2)、根据图象写出使一次函数值小于反比例函数值的的取值范围.37. 已知:点 A(1,3)是反比例函数(k≠0)的图象与直线( m≠0)的一个交点.
(1)、求这个反比例函数的表达式;(2)、根据图象写出使一次函数值小于反比例函数值的的取值范围.37. 已知:点 A(1,3)是反比例函数(k≠0)的图象与直线( m≠0)的一个交点.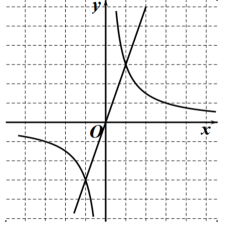 (1)、求k 、m的值:(2)、在第一象限内,当时,请直接写出x的取值范围38. 如图,在平面直角坐标系中,O为坐标原点,已知∠ACB=90°,A(0,2),C(6,2).D为等腰直角三角形ABC的边BC上一点,且S△ABC=3S△ADC.反比例函数y1=(k≠0)的图象经过点D.
(1)、求k 、m的值:(2)、在第一象限内,当时,请直接写出x的取值范围38. 如图,在平面直角坐标系中,O为坐标原点,已知∠ACB=90°,A(0,2),C(6,2).D为等腰直角三角形ABC的边BC上一点,且S△ABC=3S△ADC.反比例函数y1=(k≠0)的图象经过点D.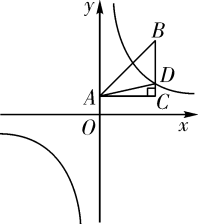 (1)、求反比例函数的解析式;(2)、若AB所在直线解析式为 , 当时,求x的取值范围.
(1)、求反比例函数的解析式;(2)、若AB所在直线解析式为 , 当时,求x的取值范围.