2022年全国中考数学真题分类汇编8 坐标系和函数
试卷更新日期:2022-12-29 类型:二轮复习
一、单选题
-
1. 若点在第一象限,则点在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限2. 中国人逢山开路,遇水架桥,靠自己勤劳的双手创造了世界奇迹.雅西高速是连接雅安和西昌的高速公路,被国内外专家学者公认为全世界自然环境最恶劣、工程难度最大、科技含量最高的山区高速公路之一,全长.一辆货车和一辆轿车先后从西昌出发驶向雅安,如图,线段表示货车离西昌距离与时间之间的函数关系:折线表示轿车离西昌距离与时间之间的函数关系,则以下结论错误的是( )
 A、货车出发1.8小时后与轿车相遇 B、货车从西昌到雅安的速度为 C、轿车从西昌到雅安的速度为 D、轿车到雅安20分钟后,货车离雅安还有20km3. 甲、乙两人沿同一直道从地到地,在整个行程中,甲、乙离地的距离与时间之间的函数关系如图所示,下列说法错误的是( )
A、货车出发1.8小时后与轿车相遇 B、货车从西昌到雅安的速度为 C、轿车从西昌到雅安的速度为 D、轿车到雅安20分钟后,货车离雅安还有20km3. 甲、乙两人沿同一直道从地到地,在整个行程中,甲、乙离地的距离与时间之间的函数关系如图所示,下列说法错误的是( ) A、甲比乙早1分钟出发 B、乙的速度是甲的速度的2倍 C、若甲比乙晚5分钟到达,则甲用时10分钟 D、若甲出发时的速度为原来的2倍,则甲比乙提前1分钟到达地4. 如图,正方形的边长为 , 将正方形绕原点O顺时针旋转45°,则点B的对应点的坐标为( )
A、甲比乙早1分钟出发 B、乙的速度是甲的速度的2倍 C、若甲比乙晚5分钟到达,则甲用时10分钟 D、若甲出发时的速度为原来的2倍,则甲比乙提前1分钟到达地4. 如图,正方形的边长为 , 将正方形绕原点O顺时针旋转45°,则点B的对应点的坐标为( ) A、 B、 C、 D、5. 函数的自变量x的取值范围是( )A、且 B、且 C、 D、且6. 两个小伙伴拿着如图的密码表玩听声音猜动物的游戏,若听到“咚咚-咚咚,咚-咚,咚咚咚-咚”表示的动物是“狗”,则听到“咚咚-咚,咚咚咚-咚咚,咚-咚咚咚”时,表示的动物是( )
A、 B、 C、 D、5. 函数的自变量x的取值范围是( )A、且 B、且 C、 D、且6. 两个小伙伴拿着如图的密码表玩听声音猜动物的游戏,若听到“咚咚-咚咚,咚-咚,咚咚咚-咚”表示的动物是“狗”,则听到“咚咚-咚,咚咚咚-咚咚,咚-咚咚咚”时,表示的动物是( ) A、狐狸 B、猫 C、蜜蜂 D、牛7. 如图,在平面直角坐标系中,将边长为2的正六边形绕点顺时针旋转个 , 得到正六边形 , 当时,正六边形的顶点的坐标是( )
A、狐狸 B、猫 C、蜜蜂 D、牛7. 如图,在平面直角坐标系中,将边长为2的正六边形绕点顺时针旋转个 , 得到正六边形 , 当时,正六边形的顶点的坐标是( ) A、 B、 C、 D、8. 如图,△ABC中,BC=6,BC边上的高为3,点D,E,F分别在边BC,AB,AC上,且EF∥BC.设点E到BC的距离为x,△DEF的面积为y,则y关于x的函数图象大致是( )
A、 B、 C、 D、8. 如图,△ABC中,BC=6,BC边上的高为3,点D,E,F分别在边BC,AB,AC上,且EF∥BC.设点E到BC的距离为x,△DEF的面积为y,则y关于x的函数图象大致是( )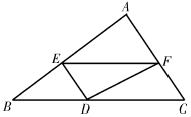 A、
A、 B、
B、 C、
C、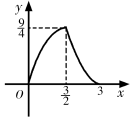 D、
D、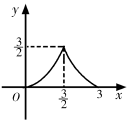 9. 如图,这是一个利用平面直角坐标系画出的某学校的示意图,如果这个坐标系分别以正东、正北方向为 轴、 轴的正方向,并且综合楼和食堂的坐标分别是 和 ,则教学楼的坐标是( )
9. 如图,这是一个利用平面直角坐标系画出的某学校的示意图,如果这个坐标系分别以正东、正北方向为 轴、 轴的正方向,并且综合楼和食堂的坐标分别是 和 ,则教学楼的坐标是( ) A、 B、 C、 D、10. 如图①,在正方形ABCD中,点M是AB的中点,点N是对角线BD上一动点,设DN=x,AN+MN=y,已知y与x之间的函数图象如图②所示,点E(a,2)是图象的最低点,那么a的值为( )
A、 B、 C、 D、10. 如图①,在正方形ABCD中,点M是AB的中点,点N是对角线BD上一动点,设DN=x,AN+MN=y,已知y与x之间的函数图象如图②所示,点E(a,2)是图象的最低点,那么a的值为( ) A、 B、2 C、 D、11. 某学校要建一块矩形菜地供学生参加劳动实践,菜地的一边靠墙,另外三边用木栏围成,木栏总长为40m.如图所示,设矩形一边长为xm,另一边长为ym,当x在一定范围内变化时,y随x的变化而变化,则y与x满足的函数关系是( )
A、 B、2 C、 D、11. 某学校要建一块矩形菜地供学生参加劳动实践,菜地的一边靠墙,另外三边用木栏围成,木栏总长为40m.如图所示,设矩形一边长为xm,另一边长为ym,当x在一定范围内变化时,y随x的变化而变化,则y与x满足的函数关系是( )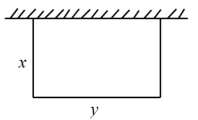 A、正比例函数关系 B、一次函数关系 C、反比例函数关系 D、二次函数关系12. 已知y1和y2均是以x为自变量的函数,当x=n时,函数值分别是N1和N2 , 若存在实数n,使得N1+N2=1,则称函数y1和y2是“和谐函数”.则下列函数y1和y2不是“和谐函数”的是( )A、y1=x2+2x和y2=﹣x+1 B、y1=和y2=x+1 C、y1=﹣和y2=﹣x﹣1 D、y1=x2+2x和y2=﹣x﹣113. 如图,等腰与矩形DEFG在同一水平线上, , 现将等腰沿箭头所指方向水平平移,平移距离x是自点C到达DE之时开始计算,至AB离开GF为止.等腰与矩形DEFG的重合部分面积记为y,则能大致反映y与x的函数关系的图象为( )
A、正比例函数关系 B、一次函数关系 C、反比例函数关系 D、二次函数关系12. 已知y1和y2均是以x为自变量的函数,当x=n时,函数值分别是N1和N2 , 若存在实数n,使得N1+N2=1,则称函数y1和y2是“和谐函数”.则下列函数y1和y2不是“和谐函数”的是( )A、y1=x2+2x和y2=﹣x+1 B、y1=和y2=x+1 C、y1=﹣和y2=﹣x﹣1 D、y1=x2+2x和y2=﹣x﹣113. 如图,等腰与矩形DEFG在同一水平线上, , 现将等腰沿箭头所指方向水平平移,平移距离x是自点C到达DE之时开始计算,至AB离开GF为止.等腰与矩形DEFG的重合部分面积记为y,则能大致反映y与x的函数关系的图象为( ) A、
A、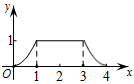 B、
B、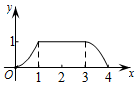 C、
C、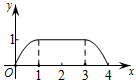 D、
D、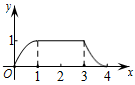 14. 2022年2月5日,电影《长津湖》在青海剧场首映,小李一家开车去观看.最初以某一速度匀速行驶,中途停车加油耽误了十几分钟,为了按时到达剧场,小李在不违反交通规则的前提下加快了速度,仍保持匀速行驶.在此行驶过程中,汽车离剧场的距离y(千米)与行驶时间t(小时)的函数关系的大致图象是( )A、
14. 2022年2月5日,电影《长津湖》在青海剧场首映,小李一家开车去观看.最初以某一速度匀速行驶,中途停车加油耽误了十几分钟,为了按时到达剧场,小李在不违反交通规则的前提下加快了速度,仍保持匀速行驶.在此行驶过程中,汽车离剧场的距离y(千米)与行驶时间t(小时)的函数关系的大致图象是( )A、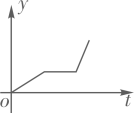 B、
B、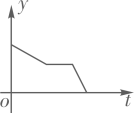 C、
C、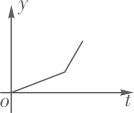 D、
D、 15. 如图所示, , , 以点A为圆心,AB长为半径画弧交x轴负半轴于点C,则点C的坐标为( )
15. 如图所示, , , 以点A为圆心,AB长为半径画弧交x轴负半轴于点C,则点C的坐标为( ) A、 B、 C、 D、16. 东东用仪器匀速向如图容器中注水,直到注满为止.用t表示注水时间,y表示水面的高度,下列图象适合表示y与t的对应关系的是( )
A、 B、 C、 D、16. 东东用仪器匀速向如图容器中注水,直到注满为止.用t表示注水时间,y表示水面的高度,下列图象适合表示y与t的对应关系的是( )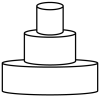 A、
A、 B、
B、 C、
C、 D、
D、 17. 如图,在▱ABCD中,∠A=60°,AB=2,AD=1,点E,F在▱ABCD的边上,从点A同时出发,分别沿A→B→C和A→D→C的方向以每秒1个单位长度的速度运动,到达点C时停止,线段EF扫过区域的面积记为y,运动时间记为x,能大致反映y与x之间函数关系的图象是( )
17. 如图,在▱ABCD中,∠A=60°,AB=2,AD=1,点E,F在▱ABCD的边上,从点A同时出发,分别沿A→B→C和A→D→C的方向以每秒1个单位长度的速度运动,到达点C时停止,线段EF扫过区域的面积记为y,运动时间记为x,能大致反映y与x之间函数关系的图象是( ) A、
A、 B、
B、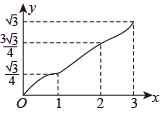 C、
C、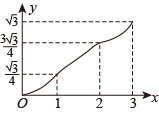 D、
D、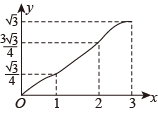 18. 如图,四边形是边长为的正方形,点E,点F分别为边 , 中点,点O为正方形的中心,连接 , 点P从点E出发沿运动,同时点Q从点B出发沿运动,两点运动速度均为 , 当点P运动到点F时,两点同时停止运动,设运动时间为 , 连接 , 的面积为 , 下列图像能正确反映出S与t的函数关系的是( )
18. 如图,四边形是边长为的正方形,点E,点F分别为边 , 中点,点O为正方形的中心,连接 , 点P从点E出发沿运动,同时点Q从点B出发沿运动,两点运动速度均为 , 当点P运动到点F时,两点同时停止运动,设运动时间为 , 连接 , 的面积为 , 下列图像能正确反映出S与t的函数关系的是( )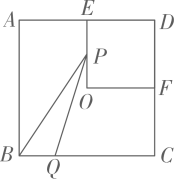 A、
A、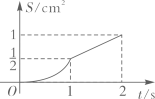 B、
B、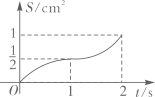 C、
C、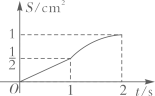 D、
D、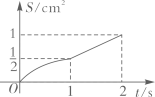 19. 如图,在中, , , , , 垂足为点 , 动点从点出发沿方向以的速度匀速运动到点 , 同时动点从点出发沿射线方向以的速度匀速运动.当点停止运动时,点也随之停止,连接 , 设运动时间为 , 的面积为 , 则下列图象能大致反映与之间函数关系的是( )
19. 如图,在中, , , , , 垂足为点 , 动点从点出发沿方向以的速度匀速运动到点 , 同时动点从点出发沿射线方向以的速度匀速运动.当点停止运动时,点也随之停止,连接 , 设运动时间为 , 的面积为 , 则下列图象能大致反映与之间函数关系的是( ) A、
A、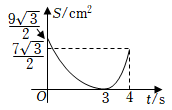 B、
B、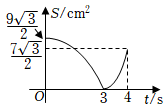 C、
C、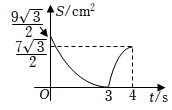 D、
D、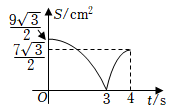 20. 如图,在中, , 动点P从点A出发,以每秒1个单位长度的速度沿线段匀速运动,当点P运动到点B时,停止运动,过点P作交于点Q,将沿直线折叠得到 , 设动点P的运动时间为t秒,与重叠部分的面积为S,则下列图象能大致反映S与t之间函数关系的是( )
20. 如图,在中, , 动点P从点A出发,以每秒1个单位长度的速度沿线段匀速运动,当点P运动到点B时,停止运动,过点P作交于点Q,将沿直线折叠得到 , 设动点P的运动时间为t秒,与重叠部分的面积为S,则下列图象能大致反映S与t之间函数关系的是( ) A、
A、 B、
B、 C、
C、 D、
D、 21. 如图,在矩形中, , 则D的坐标为( )
21. 如图,在矩形中, , 则D的坐标为( ) A、 B、 C、 D、22. 函数的自变量x的取值范围是( )A、 B、 C、且 D、23. 如图,等边、等边的边长分别为3和2.开始时点A与点D重合,在上,在上,沿向右平移,当点D到达点B时停止.在此过程中,设、重合部分的面积为y,移动的距离为x,则y与x的函数图象大致为( )
A、 B、 C、 D、22. 函数的自变量x的取值范围是( )A、 B、 C、且 D、23. 如图,等边、等边的边长分别为3和2.开始时点A与点D重合,在上,在上,沿向右平移,当点D到达点B时停止.在此过程中,设、重合部分的面积为y,移动的距离为x,则y与x的函数图象大致为( ) A、
A、 B、
B、 C、
C、 D、
D、 24. 如图,边长分别为1和2的两个正方形,其中有一条边在同一水平线上,小正方形沿该水平线自左向右匀速穿过大正方形,设穿过的时间为t,大正方形的面积为 , 小正方形与大正方形重叠部分的面积为 , 若 , 则S随t变化的函数图象大致为( )
24. 如图,边长分别为1和2的两个正方形,其中有一条边在同一水平线上,小正方形沿该水平线自左向右匀速穿过大正方形,设穿过的时间为t,大正方形的面积为 , 小正方形与大正方形重叠部分的面积为 , 若 , 则S随t变化的函数图象大致为( )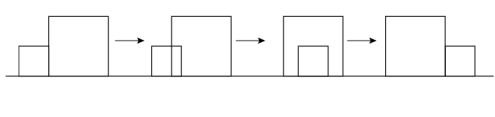 A、
A、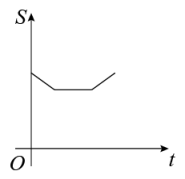 B、
B、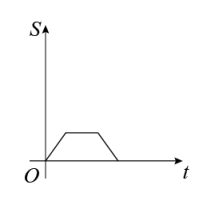 C、
C、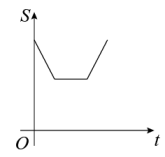 D、
D、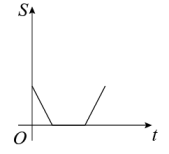 25. 如图,在△ABC中,点A(3,1),B(1,2),将△ABC向左平移2个单位,再向上平移1个单位,则点B的对应点B′的坐标为( )
25. 如图,在△ABC中,点A(3,1),B(1,2),将△ABC向左平移2个单位,再向上平移1个单位,则点B的对应点B′的坐标为( ) A、(3,-3) B、(3,3) C、(-1,1) D、(-1,3)26. 某汽车评测机构对市面上多款新能源汽车的的加速时间和满电续航里程进行了性能评测,评测结果绘制如下,每个点都对应一款新能源汽车的评测数据.已知的加速时间的中位数是 , 满电续航里程的中位数是 , 相应的直线将平面分成了①、②、③、④四个区域(直线不属于任何区域).欲将最新上市的两款新能源汽车的评测数据对应的点绘制到平面内,若以上两组数据的中位数均保持不变,则这两个点可能分别落在( )
A、(3,-3) B、(3,3) C、(-1,1) D、(-1,3)26. 某汽车评测机构对市面上多款新能源汽车的的加速时间和满电续航里程进行了性能评测,评测结果绘制如下,每个点都对应一款新能源汽车的评测数据.已知的加速时间的中位数是 , 满电续航里程的中位数是 , 相应的直线将平面分成了①、②、③、④四个区域(直线不属于任何区域).欲将最新上市的两款新能源汽车的评测数据对应的点绘制到平面内,若以上两组数据的中位数均保持不变,则这两个点可能分别落在( )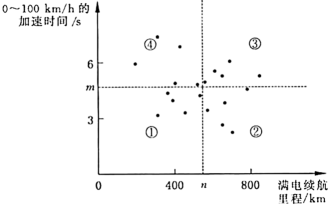 A、区域①、② B、区域①、③ C、区域①、④ D、区域③、④27. 遵义市某天的气温(单位:℃)随时间t(单位:h)的变化如图所示,设表示0时到t时气温的值的极差(即0时到时范围气温的最大值与最小值的差),则与t的函数图象大致是( )
A、区域①、② B、区域①、③ C、区域①、④ D、区域③、④27. 遵义市某天的气温(单位:℃)随时间t(单位:h)的变化如图所示,设表示0时到t时气温的值的极差(即0时到时范围气温的最大值与最小值的差),则与t的函数图象大致是( )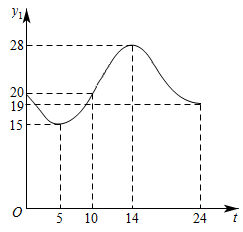 A、
A、 B、
B、 C、
C、 D、
D、
二、填空题
-
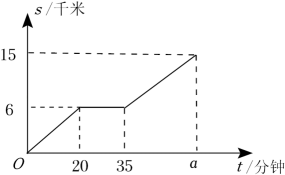
28. 周末时,达瓦在体育公园骑自行车锻炼身体,他匀速骑行了一段时间后停车休息,之后继续以原来的速度骑行.路程s(单位:千米)与时间t(单位:分钟)的关系如图所示,则图中的a= .
 29. 女子10千米越野滑雪比赛中,甲、乙两位选手同时出发后离起点的距离x(千米)与时间(分钟)之间的函数关系如图所示,则甲比乙提前分钟到达终点.
29. 女子10千米越野滑雪比赛中,甲、乙两位选手同时出发后离起点的距离x(千米)与时间(分钟)之间的函数关系如图所示,则甲比乙提前分钟到达终点. 30. 如图,在平面直角坐标系中, , , 的中点为; , , 的中点为; , , 的中点为; , , 的中点为;…;按此做法进行下去,则点的坐标为 .
30. 如图,在平面直角坐标系中, , , 的中点为; , , 的中点为; , , 的中点为; , , 的中点为;…;按此做法进行下去,则点的坐标为 .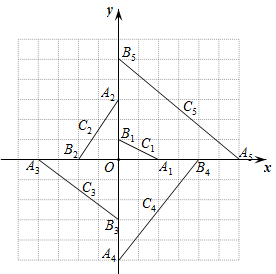 31. 如图,小刚在兰州市平面地图的部分区域建立了平面直角坐标系,如果白塔山公园的坐标是(2,2),中山桥的坐标是(3,0),那么黄河母亲像的坐标是 .
31. 如图,小刚在兰州市平面地图的部分区域建立了平面直角坐标系,如果白塔山公园的坐标是(2,2),中山桥的坐标是(3,0),那么黄河母亲像的坐标是 . 32. 若式子有意义,则实数x的取值范围是.33. 如图1,△ABC中,∠ABC=60°,D是BC边上的一个动点(不与点B,C重合),DEAB,交AC于点E,EFBC,交AB于点F.设BD的长为x,四边形BDEF的面积为y,y与x的函数图象是如图2所示的一段抛物线,其顶点P的坐标为(2,3),则AB的长为 .
32. 若式子有意义,则实数x的取值范围是.33. 如图1,△ABC中,∠ABC=60°,D是BC边上的一个动点(不与点B,C重合),DEAB,交AC于点E,EFBC,交AB于点F.设BD的长为x,四边形BDEF的面积为y,y与x的函数图象是如图2所示的一段抛物线,其顶点P的坐标为(2,3),则AB的长为 . 34. 观察如图所示的象棋棋盘,若“兵”所在的位置用(1,3)表示,“炮”所在的位置用(6,4)表示,那么“帅”所在的位置可表示为 .
34. 观察如图所示的象棋棋盘,若“兵”所在的位置用(1,3)表示,“炮”所在的位置用(6,4)表示,那么“帅”所在的位置可表示为 .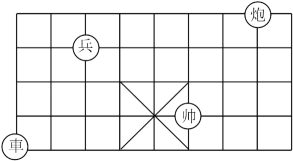
三、作图题
-
35. “水城河畔,樱花绽放,凉都宫中,书画成风”的风景,引来市民和游客争相“打卡”留念.已知水城河与南环路之间的某路段平行宽度为200米,为避免交通拥堵,请在水城河与南环路之间设计一条停车带,使得每个停车位到水城河与到凉都宫点的距离相等.
 (1)、利用尺规作出凉都宫到水城河的距离(保留作图痕迹,不写作法);
(1)、利用尺规作出凉都宫到水城河的距离(保留作图痕迹,不写作法);
(2)、在图中格点处标出三个符合条件的停车位 , , ;(3)、建立平面直角坐标系,设 , , 停车位 , 请写出与之间 关系式,在图中画出停车带,并判断点是否在停车带上.
关系式,在图中画出停车带,并判断点是否在停车带上. 四、综合题
-
36. 探究函数性质时,我们经历了列表、描点、连线画出函数图象,观察分析图象特征,概括函数性质的过程.结合已有经验,请画出函数y=-|x|的图象,并探究该函数性质.(1)、绘制函数图象
①列表:下列是x与y的几组对应值,其中a= ▲ .
x
……
﹣5
﹣4
﹣3
﹣2
﹣1
1
2
3
4
5
……
y
……
﹣3.8
﹣2.5
﹣1
1
5
5
a
﹣1
﹣2.5
﹣3.8
……
②描点:根据表中的数值描点(x,y),请补充描出点(2,a);
③连线:请用平滑的曲线顺次连接各点,画出函数图象;
 (2)、探究函数性质,请写出函数y=-|x|的一条性质:;(3)、运用函数图象及性质
(2)、探究函数性质,请写出函数y=-|x|的一条性质:;(3)、运用函数图象及性质①写出方程-|x|=5的解;
②写出不等式-|x|≤1的解集 .
37. 【发现问题】小明在练习簿的横线上取点为圆心,相邻横线的间距为半径画圆,然后半径依次增加一个间距画同心圆,描出了同心圆与横线的一些交点,如图1所示,他发现这些点的位置有一定的规律.
【提出问题】
小明通过观察,提出猜想:按此步骤继续画圆描点,所描的点都在某二次函数图象上.


 (1)、【分析问题】
(1)、【分析问题】小明利用已学知识和经验,以圆心为原点,过点的横线所在直线为轴,过点且垂直于横线的直线为轴,相邻横线的间距为一个单位长度,建立平面直角坐标系,如图2所示.当所描的点在半径为5的同心圆上时,其坐标为 .
(2)、【解决问题】请帮助小明验证他的猜想是否成立.
(3)、【深度思考】小明继续思考:设点 , 为正整数,以为直径画 , 是否存在所描的点在上.若存在,求的值;若不存在,说明理由.
38. 为加强生态文明建设,某市环保局对一企业排污情况进行检测,结果显示:所排污水中硫化物的浓度超标,即硫化物的浓度超过最高允许的1.0mg/L.环保局要求该企业立即整改,在15天内(含15天)排污达标.整改过程中,所排污水中硫化物的浓度y(mg/L)与时间x(天)的变化规律如图所示,其中线段AC表示前3天的变化规律,第3天时硫化物的浓度降为4.5mg/L.从第3天起,所排污水中硫化物的浓度y与时间x满足下面表格中的关系:时间x(天)
3
5
6
9
……
硫化物的浓度y(mg/L)
4.5
2.7
2.25
1.5
……
 (1)、在整改过程中,当0≤x<3时,硫化物的浓度y与时间x的函数表达式;(2)、在整改过程中,当x≥3时,硫化物的浓度y与时间x的函数表达式;(3)、该企业所排污水中硫化物的浓度能否在15天以内不超过最高允许的1.0mg/L?为什么?39. 如图1,在 中, , , .点D从A点出发,沿线段AB向终点B运动.过点D作AB的垂线,与 的直角边AC(或BC)相交于点E.设线段AD的长为a(cm),线段DE的长为h(cm).
(1)、在整改过程中,当0≤x<3时,硫化物的浓度y与时间x的函数表达式;(2)、在整改过程中,当x≥3时,硫化物的浓度y与时间x的函数表达式;(3)、该企业所排污水中硫化物的浓度能否在15天以内不超过最高允许的1.0mg/L?为什么?39. 如图1,在 中, , , .点D从A点出发,沿线段AB向终点B运动.过点D作AB的垂线,与 的直角边AC(或BC)相交于点E.设线段AD的长为a(cm),线段DE的长为h(cm).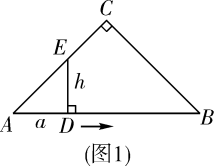 (1)、为了探究变量a与h之间的关系,对点D在运动过程中不同时刻AD,DE的长度进行测量,得出以下几组数据:
(1)、为了探究变量a与h之间的关系,对点D在运动过程中不同时刻AD,DE的长度进行测量,得出以下几组数据:变量a(cm)
0
0.5
1
1.5
2
2.5
3
3.5
4
变量h(cm)
0
0.5
1
1.5
2
1.5
1
0.5
0
在平面直角坐标系中,以变量a的值为横坐标,变量h的值为纵坐标,描点如图2-1;以变量h的值为横坐标,变量a的值为纵坐标,描点如图2-2.
根据探究的结果,解答下列问题:
①当 时, ▲ ;当 时, ▲ .
②将图2-1,图2-2中描出的点顺次连接起来.
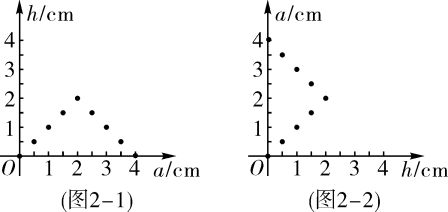
③下列说法正确的是 ▲ .(填“A”或“B”)
A.变量h是以a为自变量的函数 B.变量a是以h为自变量的函数
(2)、如图3,记线段DE与 的一直角边、斜边围成的三角形(即阴影部分)的面积 为s.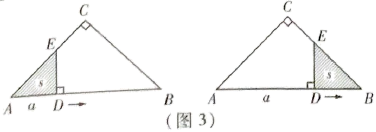
①分别求出当 和 时,s关于a的函数表达式;
②当 时,求a的值.
40. 已知A、B两地之间有一条长440千米的高速公路.甲、乙两车分别从A、B两地同时出发,沿此公路相向而行,甲车先以100千米/时的速度匀速行驶200千米后与乙车相遇,再以另一速度继续匀速行驶4小时到达B地;乙车匀速行驶至A地,两车到达各自的目的地后停止.两车距A地的路程y(千米)与各自的行驶时间x(时)之间的函数关系如图所示.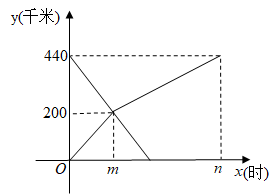 (1)、m= , n=;(2)、求两车相遇后,甲车距A地的路程y与x之间的函数关系式;(3)、当乙车到达A地时,求甲车距A地的路程.
(1)、m= , n=;(2)、求两车相遇后,甲车距A地的路程y与x之间的函数关系式;(3)、当乙车到达A地时,求甲车距A地的路程.
-