2022年全国中考数学真题分类汇编7一元一次不等式
试卷更新日期:2022-12-29 类型:二轮复习
一、单选题
-
1. 不等式组 , 的解集是( )A、 B、无解 C、 D、2. 若x=2是下列四个选项中的某个不等式组的一个解,则这个不等式组是( )A、 B、 C、 D、3. 不等式的解集在数轴上表示正确的是( )A、
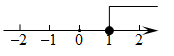 B、
B、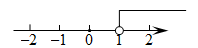 C、
C、 D、
D、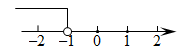 4. 若关于x的不等式组仅有3个整数解,则a的取值范围是( )A、-4≤a<-2 B、-3<a≤-2 C、-3≤a≤-2 D、-3≤a<-25. 如果点P(m,1+2m)在第三象限内,那么m的取值范围是( )A、 B、 C、 D、6. 一元一次不等式组的解集为( )A、
4. 若关于x的不等式组仅有3个整数解,则a的取值范围是( )A、-4≤a<-2 B、-3<a≤-2 C、-3≤a≤-2 D、-3≤a<-25. 如果点P(m,1+2m)在第三象限内,那么m的取值范围是( )A、 B、 C、 D、6. 一元一次不等式组的解集为( )A、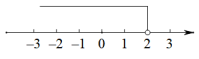 B、
B、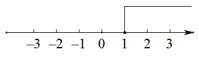 C、
C、 D、
D、 7. 关于 , 的方程组的解中与的和不小于5,则的取值范围为( )A、 B、 C、 D、8. 不等式组的解集在数轴上表示正确的是( )A、
7. 关于 , 的方程组的解中与的和不小于5,则的取值范围为( )A、 B、 C、 D、8. 不等式组的解集在数轴上表示正确的是( )A、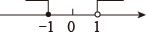 B、
B、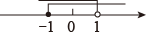 C、
C、 D、
D、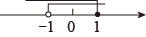 9. 与2的差不大于0,用不等式表示为( )A、 B、 C、 D、10. 若 , 则下列不等式中正确的是( )A、 B、 C、 D、11. 不等式组的解集是( )A、 B、 C、 D、12. 关于的不等式组有且只有三个整数解,则的最大值是( )A、3 B、4 C、5 D、6
9. 与2的差不大于0,用不等式表示为( )A、 B、 C、 D、10. 若 , 则下列不等式中正确的是( )A、 B、 C、 D、11. 不等式组的解集是( )A、 B、 C、 D、12. 关于的不等式组有且只有三个整数解,则的最大值是( )A、3 B、4 C、5 D、6二、填空题
-
13. 如果一元一次方程的解是一元一次不等式组的解.则称该一元一次方程为该一元一次不等式组的关联方程.若方程是关于x的不等式组的关联方程,则n的取值范围是 .14. 已知关于x的不等式组无解,则的取值范围是 .15. 若点P(m+1,m)在第四象限,则点Q(﹣3,m+2)在第象限.16. 不等式组的解集是 .17. 若关于x的一元一次不等式组的解集为 , 则a的取值范围是 .18. 不等式组的解集为 , 则m的取值范围为 .
三、多选题
-
19. 若a>b,则下列四个选项中一定成立的是( )A、a+2>b+2 B、﹣3a>﹣3b C、 > D、a﹣1<b﹣1
四、计算题
-
20. 解不等式组: , 并写出它的正整数解.21. 解不等式: .22. 解不等式组: .23.(1)、计算:;(2)、解不等式组:24. 解不等式组: .25. 解不等式组:26. 解不等式组: .
五、解答题
-
27. 解不等式组:并写出该不等式组的最大整数解.28. 解不等式组并将其解集在数轴上表示出来.
 29. 在下面给出的三个不等式中,请你任选两个组成一个不等式组,解这个不等式组,并把解集表示在数轴上.
29. 在下面给出的三个不等式中,请你任选两个组成一个不等式组,解这个不等式组,并把解集表示在数轴上.①2x﹣1<7;②5x﹣2>3(x+1);③x+3≥1﹣x.
 30. 解不等式组: , 并写出它的所有整数解.31. 解不等式组 , 并把解集在数轴上表示出来.
30. 解不等式组: , 并写出它的所有整数解.31. 解不等式组 , 并把解集在数轴上表示出来. 32. 解不等式组,并把解集在数轴上表示出来: .33. 已知方程组 的解满足 ,求k的取值范围.34. 解不等式 ,并在数轴上表示解集.
32. 解不等式组,并把解集在数轴上表示出来: .33. 已知方程组 的解满足 ,求k的取值范围.34. 解不等式 ,并在数轴上表示解集. 35. 解不等式组 , 并求出它的所有整数解的和.
35. 解不等式组 , 并求出它的所有整数解的和.六、综合题
-
36. 解答题(1)、计算: .(2)、先化简,再求值 , 其中 .(3)、求不等式组的整数解.37. 北京冬奥会吉祥物“冰墩墩”深受大家的喜爱,人们争相购买.现有甲、乙两种型号的“冰墩墩”,已知一个甲种型号比一个乙种型号多20元,购买甲、乙两种型号各10个共需1760元.(1)、求甲、乙两种型号的“冰墩墩”单价各是多少元?(2)、某团队计划用不超过4500元购买甲、乙两种型号的“冰墩墩”共50个,求最多可购买多少个甲种型号的“冰墩墩”?
-
