2022年全国中考数学真题分类汇编6 分式方程

试卷更新日期：2022-12-29 类型：二轮复习

进入出卷网下载

一、单选题

1. 《九章算术》是我国古代重要的数学专著之一，其中记录的一道题译为白话文是：把一份文件用慢马送到900里外的城市，需要的时间比规定时间多一天：如果用快马送，所需的时间比规定时间少3天．已知快马的速度是慢马的2倍，求规定时间．设规定时间为x天，则可列方程为（）

A、 $\frac{900}{x + 1} = \frac{900}{x - 3} \times 2$ B、 $\frac{900}{x + 1} \times 2 = \frac{900}{x - 3}$ C、 $\frac{900}{x - 1} = \frac{900}{x + 3} \times 2$ D、 $\frac{900}{x - 1} \times 2 = \frac{900}{x + 3}$

查看试题解析
2. 某农户承包的36亩水田和30亩旱地需要耕作．每天平均耕作旱地的亩数比耕作水田的亩数多4亩．该农户耕作完旱地所用的时间是耕作完水田所用时间的一半，求平均每天耕作水田的亩数．设平均每天耕作水田x亩，则可以得到的方程为（）

A、 $\frac{36}{x - 4} = 2 \times \frac{30}{x}$ B、 $\frac{36}{x + 4} = 2 \times \frac{30}{x}$ C、 $\frac{36}{x} = 2 \times \frac{30}{x - 4}$ D、 $\frac{36}{x} = 2 \times \frac{30}{x + 4}$

查看试题解析
3. 一辆汽车开往距出发地420km的目的地，若这辆汽车比原计划每小时多行10km，则提前1小时到达目的地．设这辆汽车原计划的速度是x km/h，根据题意所列方程是（）

A、 $\frac{420}{x} = \frac{420}{x - 10} + 1$ B、 $\frac{420}{x} + 1 = \frac{420}{x + 10}$ C、 $\frac{420}{x} = \frac{420}{x + 10} + 1$ D、 $\frac{420}{x} + 1 = \frac{420}{x - 10}$

查看试题解析
4. 若关于 $x$ 的分式方程： $2 - \frac{1 - 2 k}{x - 2} = \frac{1}{2 - x}$ 的解为正数，则 $k$ 的取值范围为（）

A、 $k < 2$ B、 $k < 2$ 且 $k \neq 0$ C、 $k > - 1$ D、 $k > - 1$ 且 $k \neq 0$

查看试题解析
5. 观察我国原油进口月度走势图，2022年4月原油进口量比2021年4月增加267万吨，当月增速为6.6%（计算方法： $\frac{267}{4036} \times 100 % \approx 6.6 %$ ）.2022年3月当月增速为 $- 14.0 %$ ，设2021年3月原油进口量为x万吨，下列算法正确的是（）

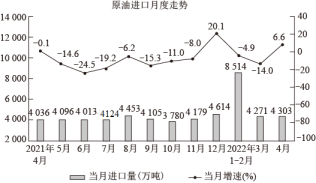A、 $\frac{x - 4271}{4271} \times 100 % = - 14.0 %$ B、 $\frac{4271 - x}{4271} \times 100 % = - 14.0 %$ C、 $\frac{x - 4271}{x} \times 100 % = - 14.0 %$ D、 $\frac{4271 - x}{x} \times 100 % = - 14.0 %$

查看试题解析
6. 八年一班学生周末乘车去红色教育基地参观学习，基地距学校60km，一部分学生乘慢车先行，出发30min后，另一部分学生乘快车前往，结果同时到达．已知快车的速度是慢车速度的1.5倍，求慢车的速度．设慢车每小时行驶xkm，根据题意，所列方程正确的是（）

A、 $\frac{60}{x}$ ﹣ $\frac{60}{1.5 x}$ ＝ $\frac{30}{60}$ B、 $\frac{60}{1.5 x}$ ﹣ $\frac{60}{x}$ ＝ $\frac{30}{60}$ C、 $\frac{60}{x}$ ﹣ $\frac{60}{1.5 x}$ ＝30 D、 $\frac{60}{1.5 x}$ ﹣ $\frac{60}{x}$ ＝30

查看试题解析
7. 一艘轮船在静水中的速度为30km/h，它沿江顺流航行144km与逆流航行96km所用时间相等，江水的流速为多少？设江水流速为vkm/h，则符合题意的方程是（）

A、 $\frac{144}{30 + v} = \frac{96}{30 - v}$ B、 $\frac{144}{30 - v} = \frac{96}{v}$ C、 $\frac{144}{30 - v} = \frac{96}{30 + v}$ D、 $\frac{144}{v} = \frac{96}{30 + v}$

查看试题解析
8. 方程 $\frac{2}{x - 3} = \frac{3}{x}$ 的解为（）

A、 $x = 3$ B、 $x = - 9$ C、 $x = 9$ D、 $x = - 3$

查看试题解析
9. 方程 $\frac{2}{x - 3} = \frac{1}{x}$ 的解是（）.

A、 $x = - 3$ B、 $x = - 1$ C、 $x = 3$ D、 $x = 1$

查看试题解析
10. 《千里江山图》是宋代王希孟的作品，如图，它的局部画面装裱前是一个长为2.4米，宽为1.4米的矩形，装裱后，整幅图画宽与长的比是8：13，且四周边衬的宽度相等，则边村的宽度应是多少米?设边衬的宽度为x米，根据题意可列方程（）

A、 $\frac{1.4 - x}{2.4 - x} = \frac{8}{13}$ B、 $\frac{1.4 + x}{2.4 + x} = \frac{8}{13}$ C、 $\frac{1.4 - 2 x}{2.4 - 2 x} = \frac{8}{13}$ D、 $\frac{1.4 + 2 x}{2.4 + 2 x} = \frac{8}{13}$

查看试题解析
11. 小明解分式方程 $\frac{1}{x + 1} = \frac{2 x}{3 x + 3} - 1$ 的过程下.
解：去分母，得                $3 = 2 x - (3 x + 3)$ .①
去括号，得                       $3 = 2 x - 3 x + 3$ .②
移项、合并同类项，得      $- x = 6$ .③
化系数为1，得                  $x = - 6$ .④
以上步骤中，开始出错的一步是（   ）

A、① B、② C、③ D、④

查看试题解析
12. 已知关于x的分式方程 $\frac{2 x - m}{x - 1} - \frac{3}{1 - x} = 1$ 的解是正数，则m的取值范围是（）

A、 $m > 4$ B、 $m < 4$ C、 $m > 4$ 且 $m \neq 5$ D、 $m < 4$ 且 $m \neq 1$

查看试题解析
13. 分式方程 $\frac{2}{x - 1} - 1 = 0$ 的解是（）

A、 $x = 1$ B、 $x = - 2$ C、 $x = 3$ D、 $x = - 3$

查看试题解析
14. 有一个容积为24 $m^{3}$ 的圆柱形的空油罐，用一根细油管向油罐内注油，当注油量达到该油罐容积的一半时，改用一根口径为细油管口径2倍的粗油管向油罐注油，直至注满，注满油的全过程共用30分钟，设细油管的注油速度为每分钟x $m^{3}$ ，由题意列方程，正确的是（）

A、 $\frac{12}{x} + \frac{12}{4 x} = 30$ B、 $\frac{15}{x} + \frac{15}{4 x} = 24$ C、 $\frac{30}{x} + \frac{30}{2 x} = 24$ D、 $\frac{12}{x} + \frac{12}{2 x} = 30$

查看试题解析
15. “爱劳动，劳动美.”甲、乙两同学同时从家里出发，分别到距家6km和10km的实践基地参加劳动.若甲、乙的速度比是 $3 ： 4$ ，结果甲比乙提前20min到达基地，求甲、乙的速度.设甲的速度为3xkm/h，则依题意可列方程为（）

A、 $\frac{6}{3 x} + \frac{1}{3} = \frac{10}{4 x}$ B、 $\frac{6}{3 x} + 20 = \frac{10}{4 x}$ C、 $\frac{6}{3 x} - \frac{10}{4 x} = \frac{1}{3}$ D、 $\frac{6}{3 x} - \frac{10}{4 x} = 20$

查看试题解析
16. 已知方程 $\frac{3 - a}{a - 4} - a = \frac{1}{4 - a}$ ，且关于x的不等式 $a < x \leq b$ 只有4个整数解，那么b的取值范围是（）

A、 $2 < b \leq 3$ B、 $3 < b \leq 4$ C、 $2 \leq b < 3$ D、 $3 \leq b < 4$

查看试题解析
17. 照相机成像应用了一个重要原理，用公式 $\frac{1}{f} = \frac{1}{μ} + \frac{1}{ν}$ (v≠f)表示，其中f表示照相机镜头的焦距，μ表示物体到镜头的距离，v表示胶片(像)到镜头的距离．已知f，v，则μ=（）

A、 $\frac{f v}{f - v}$ B、 $\frac{f - v}{f v}$ C、 $\frac{f v}{v - f}$ D、 $\frac{v - f}{f v}$

查看试题解析
18. 若关于x的方程 $\frac{2}{x}$ ＝ $\frac{m}{2 x + 1}$ 无解，则m的值为（）

A、0 B、4或6 C、6 D、0或4

查看试题解析
19. 某校购买了一批篮球和足球，已知购买足球的数量是篮球的2倍，购买足球用了5000元，购买篮球用了4000元，篮球单价比足球贵30元.根据题意可列方程 $\frac{5000}{2 x} = \frac{4000}{x}$ ﹣30，则方程中x表示（）

A、足球的单价 B、篮球的单价 C、足球的数量 D、篮球的数量

查看试题解析

二、填空题

20. 已知关于x的方程 $\frac{1}{x} + \frac{1}{x + 1} = \frac{x + a}{x (x + 1)}$ 的解为负数，则a的取值范围是．

查看试题解析
21. 分式方程 $\frac{x + 1}{2 x - 1} = 1$ 的解为．

查看试题解析
22. 对于非零实数a，b，规定a⊕b＝ $\frac{1}{a} - \frac{1}{b}$ ，若（2x﹣1）⊕2＝1，则x的值为 .

查看试题解析
23. 若关于x的分式方程 $\frac{1}{x - 2} + \frac{2}{x + 2} = \frac{x + 2 m}{x^{2} - 4}$ 的解大于1，则m的取值范围是．

查看试题解析
24. 若方程 $\frac{x - 3}{x - 2} + 1 = \frac{3}{2 - x}$ 的解使关于 $x$ 的不等式 $(2 - a) x - 3 > 0$ 成立，则实数 $a$ 的取值范围是.

查看试题解析
25. 解分式方程 $\frac{2}{x} - \frac{1}{x + 1} = 0$ 去分母时，方程两边同乘的最简公分母是.

查看试题解析
26. 方程 $\frac{2}{x} + \frac{1}{x (x - 2)} = \frac{5}{2 x}$ 的解为.

查看试题解析
27. 分式方程 $\frac{5}{x - 2} - \frac{3}{x} = 0$ 的根为

查看试题解析
28. 定义一种新运算：对于任意的非零实数a，b，a $\otimes$ b= $\frac{1}{a} + \frac{1}{b}$ ．若(x+1) $\otimes$ x= $\frac{2 x + 1}{x}$ ，则x的值为

查看试题解析

三、计算题

29.

(1)、解方程： $\frac{2}{x - 2} = \frac{1 + x}{x - 2} + 1$ ；

(2)、解不等式组： ${\begin{array}{l} x - 1 < 2 x \\ 2 (x - 3) \leq 3 - x \end{array}$ ．

查看试题解析
30. 解方程： $\frac{x}{x - 1} = \frac{x - 1}{2 x - 2}$ ．

查看试题解析
31. 解方程： $1 - \frac{2}{3 - x} = \frac{4}{x - 3}$

查看试题解析
32. 解方程： $\frac{3 - x}{x - 4} = \frac{1}{4 - x}$ .

查看试题解析

四、解答题

33. 解方程： $\frac{4}{x^{2} + x} - \frac{3}{x^{2} - x} = 0$ ．

查看试题解析
34. 为推动家乡学校篮球运动的发展，某公司计划出资12000元购买一批篮球赠送给家乡的学校．实际购买时，每个篮球的价格比原价降低了20元，结果该公司出资10000元就购买了和原计划一样多的篮球，每个篮球的原价是多少元？

查看试题解析
35. 扫地机器人具备敏捷的转弯、制动能力和强大的自主感知、规划能力，深受人们喜爱．某商场根据市场需求，采购了A，B两种型号扫地机器人．已知B型每个进价比A型的2倍少400元．采购相同数量的A，B两种型号扫地机器人，分别用了96000元和168000元．请问A，B两种型号扫地机器人每个进价分别为多少元？

查看试题解析
36. 2022年3月23日“天官课堂”第二课在中国空间站开讲了，精彩的直播激发了学生探索科学奥秘的兴趣．某中学为满足学生的需求，充实物理兴趣小组的实验项目，决定购入A、B两款物理实验套装，其中A款套装单价是B款套装单价的1.2倍，用9900元购买的A款套装数量比用7500元购买的B款套装数量多5套．求A、B两款套装的单价分别是多少元．

查看试题解析
37. 国发（2022）2号文发布后，贵州迎来了高质量快速发展，货运量持续增加.某物流公司有两种货车，已知每辆大货车的货运量比每辆小货车的货运量多4吨，且用大货车运送80吨货物所需车辆数与小货车运送60吨货物所需车辆数相同.每辆大、小货车货运量分别是多少吨？

查看试题解析
38. 科学规范戴口罩是阻断遵守病毒传播的有效措施之一，某口罩生产厂家接到一公司的订单，生产一段时间后，还剩280万个口罩未生产，厂家因更换设备，生产效率比更换设备前提高了40%.结果刚好提前2天完成订单任务.求该厂家更换设备前和更换设备后每天各生产多少万个口罩？

查看试题解析
39. 刘芳和李婷进行跳绳比赛．已知刘芳每分钟比李婷多跳20个，刘芳跳135个所用的时间与李婷跳120个所用的时间相等．求李婷每分钟跳绳的个数．

查看试题解析
40. 某中学为准备十四岁青春仪式，原计划由八年级（1）班的4个小组制作360面彩旗，后因1个小组另有任务，其余3个小组的每名学生要比原计划多做3面彩旗才能完成任务.如果这4个小组的人数相等，那么每个小组有学生多少名？

查看试题解析