2022年全国中考数学真题分类汇编5 一元二次方程（2）

试卷更新日期：2022-12-29 类型：二轮复习

进入出卷网下载

一、单选题

1. 若关于x的一元二次方程 $x^{2} - 2 m x + m^{2} - 4 m - 1 = 0$ 有两个实数根 $x_{1}$ ， $x_{2}$ ，且 $(x_{1} + 2) (x_{2} + 2) - 2 x_{1} x_{2} = 17$ ，则 $m =$ （）

A、2或6 B、2或8 C、2 D、6

查看试题解析
2. 若关于x的一元二次方程x²+6x+c＝0配方后得到方程（x+3）²＝2c，则c的值为（　　）

A、﹣3 B、0 C、3 D、9

查看试题解析
3. 已知 $x_{1}$ ， $x_{2}$ 是方程 $x^{2} - x - 2022 = 0$ 的两个实数根，则代数式 $x_{1}^{3} - 2022 x_{1} + x_{2}^{2}$ 的值是（）

A、4045 B、4044 C、2022 D、1

查看试题解析
4. 若关于 $x$ 的一元二次方程 $x^{2} + x + m = 0$ 有两个相等的实数根，则实数m的值为（）

A、-4 B、 $- \frac{1}{4}$ C、 $\frac{1}{4}$ D、4

查看试题解析
5. 某种商品原来每件售价为150元，经过连续两次降价后，该种商品每件售价为96元，设平均每次降价的百分率为x，根据随意，所列方程正确的是（）

A、 $150 (1 - x^{2}) = 96$ B、 $150 (1 - x) = 96$ C、 $150 (1 - x)^{2} = 96$ D、 $150 (1 - 2 x) = 96$

查看试题解析
6. 若 $x_{1} ， x_{2}$ 是方程 $x^{2} - 2 x - 3 = 0$ 的两个实数根，则 $x_{1} \cdot x_{2}^{2}$ 的值为（）

A、3或-9 B、-3或9 C、3或-6 D、-3或6

查看试题解析
7. 已知关于 $x$ 的一元二次方程 $x^{2} - 2 x - a = 0$ 的两根分别记为 $x_{1}$ ， $x_{2}$ ，若 $x_{1} = - 1$ ，则 $a - x_{1}^{2} - x_{2}^{2}$ 的值为（）

A、7 B、-7 C、6 D、-6

查看试题解析
8. 2022年北京冬奥会女子冰壶比赛有若干支队伍参加了单循环比赛，单循环比赛共进行了45场，共有多少支队伍参加比赛？（）

A、8 B、10 C、7 D、9

查看试题解析
9. 关于x的方程 $x^{2} - 3 k x - 2 = 0$ 实数根的情况，下列判断正确的是（）

A、有两个相等实数根 B、有两个不相等实数根 C、没有实数根 D、有一个实数根

查看试题解析
10. 一元二次方程 $x^{2} + x - 1 = 0$ 的根的情况是（）

A、有两个不相等的实数根 B、没有实数根 C、有两个相等的实数根 D、只有一个实数根

查看试题解析
11. 已知关于 $x$ 的方程 $x^{2} - (2 m - 1) x + m^{2} = 0$ 的两实数根为 $x_{1}$ ， $x_{2}$ ，若 $(x_{1} + 1) (x_{2} + 1) = 3$ ，则 $m$ 的值为（）

A、-3 B、-1 C、-3或3 D、-1或3

查看试题解析
12. 若关于 $x$ 的一元二次方程 $a x^{2} + 2 x - 1 = 0$ 有两个不相等的实数根，则 $a$ 的取值范围是（）

A、 $a \neq 0$ B、 $a > - 1$ 且 $a \neq 0$ C、 $a \geq - 1$ 且 $a \neq 0$ D、 $a > - 1$

查看试题解析
13. 已知 $m$ 、 $n$ 是一元二次方程 $x^{2} + 2 x - 5 = 0$ 的两个根，则 $m^{2} + m n + 2 m$ 的值为（）

A、0 B、-10 C、3 D、10

查看试题解析
14. 关于 $x$ 的一元二次方程 $x^{2} - 4 x + k = 0$ 无实数解，则 $k$ 的取值范围是（）

A、 $k > 4$ B、 $k < 4$ C、 $k < - 4$ D、 $k > 1$

查看试题解析
15. 下列一元二次方程有实数解的是（）

A、2x²﹣x+1＝0 B、x²﹣2x+2＝0 C、x²+3x﹣2＝0 D、x²+2＝0

查看试题解析
16. 一元二次方程 $2 x^{2} - 5 x + 6 = 0$ 的根的情况为（）

A、无实数根 B、有两个不等的实数根 C、有两个相等的实数根 D、不能判定

查看试题解析
17. 已知m为方程x²+3x﹣2022＝0的根，那么m³+2m²﹣2025m+2022的值为（）

A、﹣2022 B、0 C、2022 D、4044

查看试题解析
18. 小区新增了一家快递店，第一天揽件200件，第三天揽件242件，设该快递店揽件日平均增长率为x，根据题意，下面所列方程正确的是（）

A、 $200 {(1 + x)}^{2} = 242$ B、 $200 {(1 - x)}^{2} = 242$ C、 $200 (1 + 2 x) = 242$ D、 $200 (1 - 2 x) = 242$

查看试题解析

二、填空题

19. 方程 $x^{2} - 2 x + m = 0$ 有两个相等的实数根，则m的值为.

查看试题解析
20. 关于x的一元二次方程 $x^{2} + 2 x + t = 0$ 有两个不相等的实数根，则实数t的值为.

查看试题解析
21. 若实数a、b分别满足a²﹣4a+3＝0，b²﹣4b+3＝0，且a≠b，则 $\frac{1}{a} + \frac{1}{b}$ 的值为 .

查看试题解析
22. 已知关于 $x$ 的一元二次方程 $x^{2} + 2 x + m = 0$ 有两个不相等的实数根，则实数 $m$ 的取值范围是.

查看试题解析
23. 设 $x_{1}$ 与 $x_{2}$ 为一元二次方程 $\frac{1}{2} x^{2} + 3 x + 2 = 0$ 的两根，则 ${(x_{1} - x_{2})}^{2}$ 的值为．

查看试题解析
24. 若关于x的一元二次方程 $x^{2} - 4 x + m - 1 = 0$ 有两个不相等的实数根，则m的取值范围是．

查看试题解析
25. 一元二次方程 $x^{2} - 4 x + 3 = 0$ 配方为 ${(x - 2)}^{2} = k$ ，则k的值是.

查看试题解析
26. 请填写一个常数，使得关于 $x$ 的方程 $x^{2} - 2 x +$ $= 0$ 有两个不相等的实数根.

查看试题解析
27. 若关于 $x$ 的一元二次方程 $x^{2} - 2 x + k = 0$ 有实数根，则实数k的取值范围是.

查看试题解析
28. 设 $x_{1}$ ， $x_{2}$ 是方程 $x^{2} + 2 x - 3 = 0$ 的两个实数根，则 $x_{1}^{2} + x_{2}^{2}$ 的值为.

查看试题解析
29. 方程2x²+1=3x的解为．

查看试题解析
30. 若一元二次方程 $2 x^{2} - 4 x + m = 0$ 有两个相等的实数根，则m= ．

查看试题解析
31. 若关于 $x$ 的一元二次方程 $m x^{2} + n x - 1 = 0 (m \neq 0)$ 的一个解是 $x = 1$ ，则 $m + n$ 的值是.

查看试题解析

三、计算题

32.

(1)、解方程 $x^{2} - 2 x - 5 = 0$ ；

(2)、解不等式组： ${\begin{matrix} 2 (x + 1) > 4 \\ 3 x \leq x + 5 \end{matrix}$ .

查看试题解析
33. 解方程： $(2 x + 3)^{2} = (3 x + 2)^{2}$

查看试题解析

四、解答题

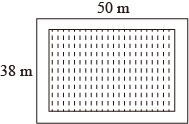
34. 如图，在长为50 m，宽为38 m的矩形地面内的四周修筑同样宽的道路，余下的铺上草坪.要使草坪的面积为1260 m² ，道路的宽应为多少？

查看试题解析

五、综合题

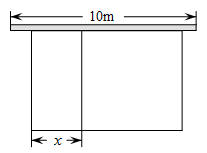
35. 某农场计划建造一个矩形养殖场，为充分利用现有资源，该矩形养殖场一面靠墙（墙的长度为10m），另外三面用栅栏围成，中间再用栅栏把它分成两个面积为1：2的矩形，已知栅栏的总长度为24m，设较小矩形的宽为xm（如图）.

(1)、若矩形养殖场的总面积为36 $m^{2}$ ，求此时x的值；

(2)、当x为多少时，矩形养殖场的总面积最大？最大值为多少？

查看试题解析
36. 已知关于 $x$ 的一元二次方程 $x^{2} - 2 x - 3 m^{2} = 0$ .

(1)、求证：方程总有两个不相等的实数根；

(2)、若方程的两个实数根分别为 $α$ ， $β$ ，且 $α + 2 β = 5$ ，求 $m$ 的值.

查看试题解析
37. 已知关于x的一元二次方程 $x^{2} + (2 k + 1) x + k^{2} + 1 = 0$ 有两个不等实数根 $x_{1}$ ， $x_{2}$ .

(1)、求k的取值范围；

(2)、若 $x_{1} x_{2} = 5$ ，求k的值.

查看试题解析
38. 建设美丽城市，改造老旧小区.某市2019年投入资金1000万元，2021年投入资金1440万元，现假定每年投入资金的增长率相同.

(1)、求该市改造老旧小区投入资金的年平均增长率；

(2)、2021年老旧小区改造的平均费用为每个80万元.2022年为提高老旧小区品质，每个小区改造费用增加15%.如果投入资金年增长率保持不变，求该市在2022年最多可以改造多少个老旧小区？

查看试题解析
39. 某造纸厂为节约木材，实现企业绿色低碳发展，通过技术改造升级，使再生纸项目的生产规模不断扩大.该厂3，4月份共生产再生纸800吨，其中4月份再生纸产量是3月份的2倍少100吨.

(1)、求4月份再生纸的产量；

(2)、若4月份每吨再生纸的利润为1000元，5月份再生纸产量比上月增加 $m %$ .5月份每吨再生纸的利润比上月增加 $\frac{m}{2} %$ ，则5月份再生纸项目月利润达到66万元.求 $m$ 的值；

(3)、若4月份每吨再生纸的利润为1200元，4至6月每吨再生纸利润的月平均增长率与6月份再生纸产量比上月增长的百分数相同，6月份再生纸项目月利润比上月增加了 $2 5%$ .求6月份每吨再生纸的利润是多少元？

查看试题解析
40. 阅读材料：
材料1：若关于x的一元二次方程ax²＋bx＋c＝0（a≠0）的两个根为x₁ ， x₂ ，则x₁＋x₂＝ $- \frac{b}{a}$ ，x₁x₂＝ $\frac{c}{a}$

材料2：已知一元二次方程x²－x－1＝0的两个实数根分别为m，n，求m²n＋mn²的值．

解：∵一元二次方程x²－x－1＝0的两个实数根分别为m，n，

∴m＋n＝1，mn＝－1，

则m²n＋mn²＝mn（m＋n）＝－1×1＝－1

根据上述材料，结合你所学的知识，完成下列问题：

(1)、材料理解：一元二次方程2x²－3x－1＝0的两个根为x₁ ， x₂ ，则x₁＋x₂＝；x₁x₂＝．

(2)、类比应用：已知一元二次方程2x²－3x－1＝0的两根分别为m、n，求 $\frac{n}{m} + \frac{m}{n}$ 的值．

(3)、思维拓展：已知实数s、t满足2s²－3s－1＝0，2t²－3t－1＝0，且s≠t，求 $\frac{1}{s} - \frac{1}{t}$ 的值．

查看试题解析