2022年全国中考数学真题分类汇编5 一元二次方程（1）

试卷更新日期：2022-12-29 类型：二轮复习

进入出卷网下载

一、单选题

1. 若关于 $x$ 的一元二次方程 $x^{2} - 2 x - k = 0$ 没有实数根，则 $k$ 的值可以是（）

A、-2 B、-1 C、0 D、1

查看试题解析
2. 若关于x的方程 $x^{2} - x - m = 0$ 有实数根，则实数m的取值的范围是（）

A、 $m < \frac{1}{4}$ B、 $m \leq \frac{1}{4}$ C、 $m \geq - \frac{1}{4}$ D、 $m > - \frac{1}{4}$

查看试题解析
3. 已知关于x的一元二次方程（m﹣1）x²+2x﹣3＝0有实数根，则m的取值范围是（）

A、m≥ $\frac{2}{3}$ B、m＜ $\frac{2}{3}$ C、m＞ $\frac{2}{3}$ 且m≠1 D、m≥ $\frac{2}{3}$ 且m≠1

查看试题解析
4. 对于实数 $a$ ， $b$ 定义新运算： $a ※ b = a b^{2} - b$ ，若关于 $x$ 的方程 $1 ※ x = k$ 有两个不相等的实数根，则 $k$ 的取值范围（）

A、 $k > - \frac{1}{4}$ B、 $k < - \frac{1}{4}$ C、 $k > - \frac{1}{4}$ 且 $k \neq 0$ D、 $k \geq - \frac{1}{4}$ 且 $k \neq 0$

查看试题解析
5. 受国际油价影响，今年我国汽油价格总体呈上升趋势．某地92号汽油价格三月底是6.2元/升，五月底是8.9元/升．设该地92号汽油价格这两个月平均每月的增长率为 $x$ ，根据题意列出方程，正确的是（）

A、 $6.2 (1 + x)^{2} = 8.9$ B、 $8.9 (1 + x)^{2} = 6.2$ C、 $6.2 (1 + x^{2}) = 8.9$ D、 $6.2 (1 + x) + 6.2 (1 + x)^{2} = 8.9$

查看试题解析
6. 李师傅家的超市今年1月盈利3000元，3月盈利3630元．若从1月到3月，每月盈利的平均增长率都相同，则这个平均增长率是（）

A、10.5% B、10% C、20% D、21%

查看试题解析
7. 定义新运算 $a * b$ ：对于任意实数 $a$ ， $b$ 满足 $a * b = (a + b) (a - b) - 1$ ，其中等式右边是通常的加法、减法、乘法运算，例如 $3 * 2 = (3 + 2) (3 - 2) - 1 = 5 - 1 = 4$ ．若 $x * k = 2 x$ （ $k$ 为实数）是关于 $x$ 的方程，则它的根的情况是（）

A、有一个实数根 B、有两个不相等的实数根 C、有两个相等的实数根 D、没有实数根

查看试题解析
8. 若x＝﹣1是方程x²+x+m＝0的一个根，则此方程的另一个根是（）

A、﹣1 B、0 C、1 D、2

查看试题解析
9. 关于x的一元二次方程 $2 x^{2} + x - k = 0$ 没有实数根，则k的取值范围是（）

A、 $k < - \frac{1}{8}$ B、 $k \leq - \frac{1}{8}$ C、 $k > - \frac{1}{8}$ D、 $k \geq - \frac{1}{8}$

查看试题解析
10. 关于x的一元二次方程 $k x^{2} + 2 x - 1 = 0$ 有两个相等的实数根，则 $k =$ （）

A、-2 B、-1 C、0 D、1

查看试题解析
11. 下列说法正确的是（）
①若二次根式 $\sqrt{1 - x}$ 有意义，则x的取值范围是x≥1．
②7＜ $\sqrt{65}$ ＜8．
③若一个多边形的内角和是540°，则它的边数是5．
④ $\sqrt{16}$ 的平方根是±4．
⑤一元二次方程x²﹣x﹣4＝0有两个不相等的实数根．

A、①③⑤ B、③⑤ C、③④⑤ D、①②④

查看试题解析
12. 若关于x的一元二次方程 $x^{2} + 6 x + c = 0$ 有两个相等的实数根，则c的值是（）

A、36 B、9 C、6 D、 $- 9$

查看试题解析
13. 某厂家今年一月份的口罩产量是30万个，三月份的口罩产量是50万个，若设该厂家一月份到三月份的口罩产量的月平均增长率为x.则所列方程为（）

A、30（1+x）²＝50 B、30（1﹣x）²＝50 C、30（1+x²）＝50 D、30（1﹣x²）＝50

查看试题解析
14. 一元二次方程 $2 x^{2} + x - 1 = 0$ 的根的情况是（）

A、有两个不相等的实数根 B、有两个相等的实数根 C、只有一个实数根 D、没有实数根

查看试题解析
15. 用配方法解一元二次方程 $3 x^{2} + 6 x - 1 = 0$ 时，将它化为 ${(x + a)}^{2} = b$ 的形式，则a+b的值为（）

A、 $\frac{10}{3}$ B、 $\frac{7}{3}$ C、2 D、 $\frac{4}{3}$

查看试题解析
16. 若 $x = - 2$ 是一元二次方程 $x^{2} + 2 x + m = 0$ 的一个根，则方程的另一个根及m的值分别是（）

A、0，-2 B、0，0 C、-2，-2 D、-2，0

查看试题解析
17. 一元二次方程 $x^{2} + 4 x - 8 = 0$ 的解是（）

A、 $x_{1} = 2 + 2 \sqrt{3} ， x_{2} = 2 - 2 \sqrt{3}$ B、 $x_{1} = 2 + 2 \sqrt{2} ， x_{2} = 2 - 2 \sqrt{2}$ C、 $x_{1} = - 2 + 2 \sqrt{2} ， x_{2} = - 2 - 2 \sqrt{2}$ D、 $x_{1} = - 2 + 2 \sqrt{3} ， x_{2} = - 2 - 2 \sqrt{3}$

查看试题解析

二、填空题

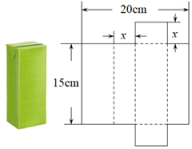
18. 将一个容积为360cm³的包装盒剪开铺平，纸样如图所示．利用容积列出图中x（cm）满足的一元二次方程：（不必化简）．

查看试题解析
19. 若一元二次方程x²＋x－c＝0没有实数根，则c的取值范围是．

查看试题解析
20. $α$ 、 $β$ 是关于 $x$ 的方程 $x^{2} - x + k - 1 = 0$ 的两个实数根，且 $α^{2} - 2 α - β = 4$ ，则 $k$ 的值为．

查看试题解析
21. 已知关于 $x$ 的一元二次方程 $x^{2} - 4 x + m = 0$ 有两个相等的实数根，则 $m =$ ．

查看试题解析
22. 若a是一元二次方程 $x^{2} + 2 x - 3 = 0$ 的一个根，则 $2 a^{2} + 4 a$ 的值是．

查看试题解析
23. 关于x的一元二次方程2x²+4mx+m=0有两个不同的实数根x₁ ， x₂ ，且 $x_{1}^{2} + x_{2}^{2} = \frac{3}{16}$ ，则m= ．

查看试题解析
24. 若关于x的一元二次方程x2+3x+m=0有实数根，则m的取值范围是．

查看试题解析
25. 如图，小明同学用一张长11cm，宽7cm的矩形纸板制作一个底面积为 $21 c m^{2}$ 的无盖长方体纸盒，他将纸板的四个角各剪去一个同样大小的正方形，将四周向上折叠即可（损耗不计）．设剪去的正方形边长为xcm，则可列出关于x的方程为．

查看试题解析
26. 已知x²- $2 \sqrt{3}$ x+m=0有两个不相等的实数根，则m的取值范围是．

查看试题解析
27. 某公司5月份的营业额为25万，7月份的营业额为36万，已知5、6月的增长率相同，则增长率为．

查看试题解析
28. 已知一元二次方程 $x^{2} + 6 x + m = 0$ 有两个相等的实数根，则m的值为．

查看试题解析
29. 若关于x的方程 $x^{2} + x + c = 0$ 有两个相等的实数根，则实数c的值为．

查看试题解析
30. 若关于x的方程 $x^{2} - 3 x + m = 0$ 有两个不相等的实数根，且 $m \geq - 3$ ，则从满足条件的所有整数m中随机选取一个，恰好是负数的概率是．

查看试题解析
31. 关于x的一元二次方程 $(k - 1) x^{2} - 2 x + 1 = 0$ 有两个不相等的实数根，则k的取值范围是．

查看试题解析
32. 已知x₁、x₂是关于x的方程x²﹣2x+k﹣1＝0的两实数根，且 $\frac{x_{2}}{x_{1}} + \frac{x_{1}}{x_{2}}$ ＝x₁²+2x₂﹣1，则k的值为 .

查看试题解析

三、计算题

33.

(1)、解方程： $x^{2} - 2 x - 1 = 0$ ；

(2)、解不等式组： ${\begin{array}{l} 2 x - 1 \geq 1 ， \\ \frac{1 + x}{3} < x - 1 . \end{array}$

查看试题解析

四、综合题

34. 阅读材料，解答问题：
材料1

为了解方程 ${(x^{2})}^{2} - 13 x^{2} + 36 = 0$ ，如果我们把 $x^{2}$ 看作一个整体，然后设 $y = x^{2}$ ，则原方程可化为 $y^{2} - 13 y + 36 = 0$ ，经过运算，原方程的解为 $x_{1 ， 2} = \pm 2$ ， $x_{3 ， 4} = \pm 3$ ．我们把以上这种解决问题的方法通常叫做换元法．

材料2

已知实数m，n满足 $m^{2} - m - 1 = 0$ ， $n^{2} - n - 1 = 0$ ，且 $m \neq n$ ，显然m，n是方程 $x^{2} - x - 1 = 0$ 的两个不相等的实数根，由书达定理可知 $m + n = 1$ ， $m n = - 1$ ．

根据上述材料，解决以下问题：

(1)、直接应用：
方程 $x^{4} - 5 x^{2} + 6 = 0$ 的解为；

(2)、间接应用：
已知实数a，b满足： $2 a^{4} - 7 a^{2} + 1 = 0$ ， $2 b^{4} - 7 b^{2} + 1 = 0$ 且 $a \neq b$ ，求 $a^{4} + b^{4}$ 的值；

(3)、拓展应用：
已知实数m，n满足： $\frac{1}{m^{4}} + \frac{1}{m^{2}} = 7$ ， $n^{2} - n = 7$ 且 $n > 0$ ，求 $\frac{1}{m^{4}} + n^{2}$ 的值．

查看试题解析
35. 如图，用一根长60厘米的铁丝制作一个“日”字型框架ABCD，铁丝恰好全部用完．

(1)、若所围成矩形框架ABCD的面积为144平方厘米，则AB的长为多少厘米？

(2)、矩形框架ABCD面积最大值为平方厘米．

查看试题解析
36. 已知T= ${(a + 3 b)}^{2} + (2 a + 3 b) (2 a - 3 b) + a^{2}$

(1)、化简T；

(2)、若关于x的方程 $x^{2} + 2 a x - a b + 1 = 0$ 有两个相等的实数根，求T的值．

查看试题解析
37.

(1)、a，b两个实数在数轴上的对应点如图所示.
用“<”或“>”填空：ab，ab0；

(2)、在初中阶段我们已经学习了一元二次方程的三种解法，他们分别是配方法、公式法和因式分解法，请从下列一元二次方程中任选两个，并解这两个方程.
①x²+2x−1=0；②x²−3x=0；③x²−4x=4；④x²−4=0.

查看试题解析