2022年全国中考数学真题分类汇编4 一次方程问题

试卷更新日期：2022-12-29 类型：二轮复习

进入出卷网下载

一、单选题

1. 某班环保小组收集废旧电池，数据统计如下表．问1节5号电池和1节7号电池的质量分别是多少？设1节5号电池的质量为x克，1节7号电池的质量为y克，列方程组，由消元法可得x的值为（）

	5号电池（节）	7号电池（节）	总质量（克）
第一天	2	2	72
第二天	3	2	96

A、12 B、16 C、24 D、26

查看试题解析

2. 我国“DF－41型”导弹俗称“东风快递”，速度可达到26马赫（1马赫＝340米/秒），则“DF－41型”导弹飞行多少分钟能打击到12000公里处的目标？设飞行 $x$ 分钟能打击到目标，可以得到方程（）

A、 $26 \times 340 \times 60 x = 12000$ B、 $26 \times 340 x = 12000$ C、 $\frac{26 \times 340 x}{1000} = 12000$ D、 $\frac{26 \times 340 \times 60 x}{1000} = 12000$

查看试题解析
3. 小明解方程 $\frac{x + 1}{2} - 1 = \frac{x - 2}{3}$ 的步骤如下：
解：方程两边同乘6，得 $3 (x + 1) - 1 = 2 (x - 2)$ ①
去括号，得 $3 x + 3 - 1 = 2 x - 2$ ②
移项，得 $3 x - 2 x = - 2 - 3 + 1$ ③
合并同类项，得 $x = - 4$ ④
以上解题步骤中，开始出错的一步是（）

A、① B、② C、③ D、④

查看试题解析
4. 在数学活动课上，兴趣小组的同学用一根质地均匀的轻质木杆和若干个钩码做实验．如图所示，在轻质木杆O处用一根细线悬挂，左端A处挂一重物，右端B处挂钩码，每个钩码质量是50g．若OA=20cm，OB=40cm，挂3个钩码可使轻质木杆水平位置平衡．设重物的质量为xg，根据题意列方程得（）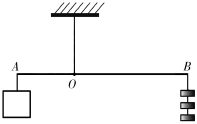

A、 $20 x = 40 \times 50 \times 3$ B、 $40 x = 20 \times 50 \times 3$ C、 $3 \times 20 x = 40 \times 50$ D、 $3 \times 40 x = 20 \times 50$

查看试题解析
5. 《孙子算经》是中国传统数学的重要著作，其中有一道题，原文是：“今有木，不知长短，引绳度之，余绳四尺五寸；屈绳量之，不足一尺．木长几何？”意思是：用一根绳子去量一根木头的长，绳子还剩余4.5尺；将绳子对折再量木头，则木头还剩余1尺，问木头长多少尺？可设木头长为x尺，绳子长为y尺，则所列方程组正确的是（）

A、 ${\begin{array}{l} y - x = 4.5 \\ 2 x - y = 1 \end{array}$ B、 ${\begin{array}{l} x - y = 4.5 \\ 2 x - y = 1 \end{array}$ C、 ${\begin{array}{l} x - y = 4.5 \\ \frac{y}{2} - x = 1 \end{array}$ D、 ${\begin{array}{l} y - x = 4.5 \\ x - \frac{y}{2} = 1 \end{array}$

查看试题解析
6. 下列说法中，正确的是（）

A、若 $a c = b c$ ，则 $a = b$ B、若 $a^{2} = b^{2}$ ，则 $a = b$ C、若 $\frac{a}{c} = \frac{b}{c}$ ，则 $a = b$ D、若 $- \frac{1}{3} x = 6$ ，则 $x = 2$

查看试题解析
7. 张三经营了一家草场，草场里面种植上等草和下等草．他卖五捆上等草的根数减去11根，就等下七捆下等草的根数；卖七捆上等草的根数减去25根，就等于五捆下等草的根数．设上等草一捆为 $x$ 根，下等草一捆为 $y$ 根，则下列方程正确的是（）

A、 ${\begin{array}{l} 5 y - 11 = 7 x \\ 7 y - 25 = 5 x \end{array}$ B、 ${\begin{array}{l} 5 x + 11 = 7 y \\ 7 x + 25 = 5 y \end{array}$ C、 ${\begin{array}{l} 5 x - 11 = 7 y \\ 7 x - 25 = 5 y \end{array}$ D、 ${\begin{array}{l} 7 x - 11 = 5 y \\ 5 x - 25 = 7 y \end{array}$

查看试题解析
8. 《九章算术》是中国传统数学重要的著作，奠定了中国传统数学的基本框架，其中《盈不足》卷记载了一道有趣的数学问题：“今有共买物，人出八，赢三；人出七，不足四，问人数、物价各几何？”译文：“今有人合伙购物，每人出8钱，会多出3钱；每人出7钱，又差4钱，问人数，物价各多少？”设人数为x人，物价为y钱，根据题意，下面所列方程组正确的是（）

A、 ${\begin{array}{l} 8 x + 3 = y \\ 7 x - 4 = y \end{array}$ B、 ${\begin{array}{l} 8 x - 3 = y \\ 7 x + 4 = y \end{array}$ C、 ${\begin{array}{l} 8 x + 3 = y \\ 7 x + 4 = y \end{array}$ D、 ${\begin{array}{l} 8 x - 3 = y \\ 7 x - 4 = y \end{array}$

查看试题解析
9. 植树节当天，七年级1班植树300棵，正好占这批树苗总数的 $\frac{3}{5}$ ，七年级2班植树棵数是这批树苗总数的 $\frac{1}{5}$ ，则七年级2班植树的棵数是（）

A、36 B、60 C、100 D、180

查看试题解析
10. 方程3x＝2x＋7的解是（）

A、x＝4 B、x＝﹣4 C、x＝7 D、x＝﹣7

查看试题解析
11. 中国清代算书《御制数理精蕴》中有这样一题：“马四匹、牛六头，共价四十八两（我国古代货币单位）；马三匹、牛五头，共价三十八两，问马、牛各价几何？”设马每匹x两，牛每头y两，根据题意可列方程组为（）

A、 ${\begin{array}{l} 6 x + 4 y = 48 ， \\ 5 x + 3 y = 38 \end{array}$ B、 ${\begin{array}{l} 6 x + 4 y = 38 ， \\ 5 x + 3 y = 48 \end{array}$ C、 ${\begin{array}{l} 4 x + 6 y = 48 \\ 3 x + 5 y = 38 \end{array}$ D、 ${\begin{array}{l} 4 x + 6 y = 38 ， \\ 3 x + 5 y = 48 \end{array}$

查看试题解析
12. 若代数式 $x + 1$ 的值为6，则x等于（）

A、5 B、-5 C、7 D、-7

查看试题解析
13. 我国古代数学著作《孙子算经》中有这样一道题，原文如下：今有百鹿入城，家取一鹿，不尽，又三家共一鹿，适尽，问：城中家几何？大意为：今有100头鹿进城，每家取一头鹿，没有取完，剩下的鹿每3家共取一头，恰好取完，问：城中有多少户人家？在这个问题中，城中人家的户数为（）

A、25 B、75 C、81 D、90

查看试题解析
14. 五一小长假，小华和家人到公园游玩.湖边有大小两种游船.小华发现1艘大船与2艘小船一次共可以满载游客32人，2艘大船与1艘小船一次共可以满载游客46人.则1艘大船与1艘小船一次共可以满载游客的人数为（）

A、30 B、26 C、24 D、22

查看试题解析
15. 为培养青少年的创新意识、动手实践能力、现场应变能力和团队精神，湘潭市举办了第10届青少年机器人竞赛.组委会为每个比赛场地准备了四条腿的桌子和三条腿的凳子共12个，若桌子腿数与凳子腿数的和为40条，则每个比赛场地有几张桌子和几条凳子？设有x张桌子，有y条凳子，根据题意所列方程组正确的是（）

A、 ${\begin{array}{l} x + y = 40 \\ 4 x + 3 y = 12 \end{array}$ B、 ${\begin{array}{l} x + y = 12 \\ 4 x + 3 y = 40 \end{array}$ C、 ${\begin{array}{l} x + y = 40 \\ 3 x + 4 y = 12 \end{array}$ D、 ${\begin{array}{l} x + y = 12 \\ 3 x + 4 y = 40 \end{array}$

查看试题解析

二、填空题

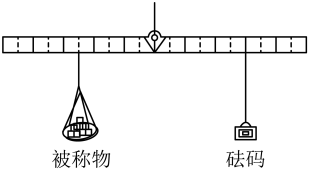
16. 《九章算术》中记载，战国时期的铜衡杆，其形式既不同于天平衡杆，也异于称杆衡杆正中有拱肩提纽和穿线孔，一面刻有贯通上、下的十等分线．用该衡杆称物，可以把被称物与砝码放在提纽两边不同位置的刻线上，这样，用同一个砝码就可以称出大于它一倍或几倍重量的物体．图为铜衡杆的使用示意图，此时被称物重量是砝码重量的倍．

查看试题解析
17. 如图，圆中扇子对应的圆心角 $α$ （ $α < 180 °$ ）与剩余圆心角 $β$ 的比值为黄金比时，扇子会显得更加美观，若黄金比取0.6，则 $β - α$ 的度数是．

查看试题解析
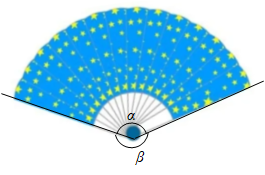18. 我国古代数学经典著作《九章算术》中有这样一题，原文是：“今有共买物，人出八，盈三，人出七，不足四，问人数，物价各几何？”意思是：今有人合伙购物，每人出八钱，会多三钱；每人出七钱，又差四钱．问人数、物价各多少？设人数为x人，物价为y钱，可列方程组为
．

查看试题解析
19. 《九章算术》中记载：“今有共买羊，人出五，不足四十五；人出七，余三．问人数、羊价各几何？”其大意是：今有人合伙买羊，若每人出5钱，还差45钱；若每人出7钱，多余3钱。问人数、羊价各是多少？若设人数为x，则可列方程为．

查看试题解析
20. 二元一次方程组 ${\begin{array}{l} x + 2 y = 5 \\ y = 2 x \end{array}$ 的解是．

查看试题解析
21. 《九章算术》是人类科学史上应用数学的“算经之首”，其书中卷八方程[七]中记载：“今有牛五、羊二，直金十两．牛二、羊五，直金八两．牛、羊各直金几何？”题目大意是：“5头牛、2只羊共值金10两.2头牛、5只羊共值金8两，每头牛、每只羊各值金多少两？”根据题意，可求得1头牛和1只羊共值金两．

查看试题解析
22. 我国古代著作《九章算术》中记载了这样一个问题：“今有共买豕，人出一百，盈一百；人出九十，适足．”其大意是：“今有人合伙买猪，每人出100钱，则会多出100钱；每人出90钱，恰好合适．”若设共有x人，根据题意，可列方程为．

查看试题解析
23. 《算法统宗》是中国古代重要的数学著作，其中记载：我问开店李三公，众客都来到店中，一房七客多七客，一房九客一房空．其大意为：今有若干人住店，若每间住7人，则余下7人无房可住；若每间住9人，则余下一间无人住，设店中共有x间房，可求得x的值为．

查看试题解析
24. 方程组 ${\begin{array}{l} 2 x + 3 y = 13 \\ 3 x - 2 y = 0 \end{array}$ 的解为．

查看试题解析
25. 有大小两种货车，3辆大货车与4辆小货车一次可以运货22吨，5辆大货车与2辆小货车一次可以运货25吨，则4辆大货车与3辆小货车一次可以运货吨.

查看试题解析
26. 已知 ${\begin{array}{l} x = 1 \\ y = 2 \end{array}$ 是方程ax+by＝3的解，则代数式2a+4b﹣5的值为 .

查看试题解析
27. 《九章算术》中记载了一道数学问题，其译文为：有大小两种盛酒的桶，已知5个大桶加上1个小桶可以盛酒3斛（斛，音hú，是古代一种容量单位），1个大桶加上5个小桶可以盛酒2斛.1个大桶、1个小桶分别可以盛酒多少斛？设1个大桶可以盛酒 $x$ 斛、1个小桶可以盛酒 $y$ 斛．根据题意，可列方程组为．

查看试题解析
28. 二元一次方程组 ${\begin{matrix} 3 x + 2 y = 12 \\ 2 x - y = 1 \end{matrix}$ 的解为.

查看试题解析
29. 若实数m，n满足 $∣ m - n - 5 ∣ + \sqrt{2 m + n - 4} = 0$ ，则 $3 m + n =$ .

查看试题解析
30. 阅读材料：整体代值是数学中常用的方法.例如“已知 $3 a - b = 2$ ，求代数式 $6 a - 2 b - 1$ 的值.”可以这样解： $6 a - 2 b - 1 = 2 (3 a - b) - 1 = 2 \times 2 - 1 = 3$ .根据阅读材料，解决问题：若 $x = 2$ 是关于x的一元一次方程 $a x + b = 3$ 的解，则代数式 $4 a^{2} + 4 a b + b^{2} + 4 a + 2 b - 1$ 的值是.

查看试题解析
31. 若 ${(2 x + y - 5)}^{2} + \sqrt{x + 2 y + 4} = 0$ ，则 $x - y$ 的值是.

查看试题解析
32. 已知二元一次方程组 ${\begin{array}{l} x + 2 y = 4 \\ 2 x + y = 5 \end{array}$ ，则 $x - y$ 的值为.

查看试题解析

三、计算题

33. 解方程组： ${\begin{array}{l} x - y = 2 ① \\ 2 x + y = 7 ② \end{array}$ ．

查看试题解析
34. 解二元一次方程组： ${\begin{array}{l} x - y = 1 \\ x + y = 3 \end{array}$ .

查看试题解析
35.

(1)、计算： ${(- 3)}^{2} \times 3^{- 1} + (- 5 + 2) + | - 2 |$ ；

(2)、解方程组： ${\begin{array}{l} 2 x - y = 3 ① \\ x + y = 6 ② \end{array}$ ．

查看试题解析

四、解答题

36. 某公司专业生产某种产品，6月初（当月月历如图）接到一份求购5000件该产品的订单，要求本月底完成，7月1日按期交货．

日	一	二	三	四	五	六
			1	2	3	4
5	6	7	8	9	10	11
12	13	14	15	16	17	18
19	20	21	22	23	24	25
26	27	28	29	30

经盘点目前公司已有该产品库存2855件，补充原材料后，从本月7日开始生产剩余数量的该产品，已知该公司除周六、周日正常休息外，每天的生产量相同．但因受高温天气影响，从本月10日开始，每天的生产量比原来减少了25件，截止到17日生产结束，库存总量达3830件．如果按照10日开始的生产速度继续生产该产品，能否按期完成订单？请说明理由．如果不能，请你给该公司生产部门提出一个合理的建议，以确保能按期交货．

查看试题解析

37. 2022年北京冬奥会吉祥物冰墩墩和冬残奥会吉祥物雪容融深受大家喜爱．已知购买1个冰墩墩毛绒玩具和2个雪容融毛绒玩具用了400元，购买3个冰墩墩毛绒玩具和4个雪容融毛绒玩具用了1000元．这两种毛绒玩具的单价各是多少元？

查看试题解析
38. 我省某村委会根据“十四五”规划的要求，打造乡村品牌，推销有机黑胡椒和有机白胡椒.已知每千克有机黑胡椒比每千克有机白胡椒的售价便宜10元，购买2千克有机黑胡椒和3千克有机白胡椒需付280元，求每千克有机黑胡椒和每千克有机白胡椒的售价.

查看试题解析
39. 《九章算术》是我国古代的数学专著，几名学生要凑钱购买1本．若每人出8元，则多了3元；若每人出7元，则少了4元．问学生人数和该书单价各是多少？

查看试题解析

五、综合题

40. 《孙子算经》是中国古代重要的数学著作，该书第三卷记载：“今有兽六首四足，禽四首二足，上有七十六首，下有四十六足，问禽、兽各几何？”译文：今有一种6头4脚的兽与一种4头2脚的鸟，若兽与鸟共有76个头与46只脚．问兽、鸟各有多少？
根据译文，解决下列问题：

(1)、设兽有x个，鸟有y只，可列方程组为；

(2)、求兽、鸟各有多少．

查看试题解析

日	一	二	三	四	五	六
			1	2	3	4
5	6	7	8	9	10	11
12	13	14	15	16	17	18
19	20	21	22	23	24	25
26	27	28	29	30

日	一	二	三	四	五	六
			1	2	3	4
5	6	7	8	9	10	11
12	13	14	15	16	17	18
19	20	21	22	23	24	25
26	27	28	29	30

日	一	二	三	四	五	六
			1	2	3	4
5	6	7	8	9	10	11
12	13	14	15	16	17	18
19	20	21	22	23	24	25
26	27	28	29	30