27.2.2相似三角形的性质 人教版九年级下册同步练习
试卷更新日期:2022-12-28 类型:同步测试
一、单选题
-
1. 的三边长分别为2,3,4,另有一个与它相似的三角形 , 其最长边为16,则的周长是( )A、54 B、36 C、27 D、212. 如图,在中,点D,E分别在上, , 如果 , 那么( )
 A、 B、 C、 D、3. 如图,一块等腰直角三角板,它的斜边BC=8cm,内部△DEF的各边与OABC的各边分别平行,且它的斜边EF=4cm,则△DEF的面积与阴影部分的面积比为( )
A、 B、 C、 D、3. 如图,一块等腰直角三角板,它的斜边BC=8cm,内部△DEF的各边与OABC的各边分别平行,且它的斜边EF=4cm,则△DEF的面积与阴影部分的面积比为( ) A、1:2 B、1:3 C、1:4 D、1:84. 如图,比例规是伽利略发明的一种画图工具,使用它可以把线段按一定比例伸长或缩短,它是由长度相等的两脚和交叉构成的.如果把比例规的两脚合上,用螺丝钉固定点O的位置,使 , 然后张开两脚,使点A,B两个尖端分别在线段l的两个端点上,若 , 则的长是( )
A、1:2 B、1:3 C、1:4 D、1:84. 如图,比例规是伽利略发明的一种画图工具,使用它可以把线段按一定比例伸长或缩短,它是由长度相等的两脚和交叉构成的.如果把比例规的两脚合上,用螺丝钉固定点O的位置,使 , 然后张开两脚,使点A,B两个尖端分别在线段l的两个端点上,若 , 则的长是( ) A、5cm B、10 cm C、15 cm D、20 cm5. 如图,在中, , 中线 , 相交于点F, , 交于点G, , 则的长为( )
A、5cm B、10 cm C、15 cm D、20 cm5. 如图,在中, , 中线 , 相交于点F, , 交于点G, , 则的长为( ) A、12 B、16 C、20 D、246. 如图,在▱ABCD中,点E在对角线BD上,EM∥AD,交AB于点M,EN∥AB,交AD于点N,则下列式子一定正确的是( )
A、12 B、16 C、20 D、246. 如图,在▱ABCD中,点E在对角线BD上,EM∥AD,交AB于点M,EN∥AB,交AD于点N,则下列式子一定正确的是( ) A、 B、 C、 D、7. 如图,在平行四边形ABCD中,点E在AD上,连接CE并延长交 BA延长线于点F,若AE:AD=2:3,CD=3cm,则AF的长为( )
A、 B、 C、 D、7. 如图,在平行四边形ABCD中,点E在AD上,连接CE并延长交 BA延长线于点F,若AE:AD=2:3,CD=3cm,则AF的长为( )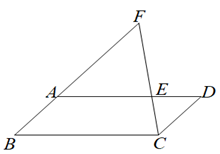 A、5cm B、6cm C、7cm D、8cm8. 如图,在△ABC中,D,E分别是边AC,AB的中点,BD与CE相交于点O,连结DE.有下列结论:①;②;③;④.其中正确的个数是( )
A、5cm B、6cm C、7cm D、8cm8. 如图,在△ABC中,D,E分别是边AC,AB的中点,BD与CE相交于点O,连结DE.有下列结论:①;②;③;④.其中正确的个数是( ) A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
9. 若两个相似三角形的一组对应边长分别为16和32,它们的周长之差为36,则较小三角形的周长是.10. 如图,在边长为1的正方形网格中,点A,B,C,D都在格点处,线段与相交于点E,则的值为 .
 11. 如图,在中,点D、E分别在边、上, . 已知 , , 则的长是 .
11. 如图,在中,点D、E分别在边、上, . 已知 , , 则的长是 . 12. 如图:正方形DGFE的边EF在△ABC边BC上,顶点D、G分别在边AB、AC上,AH⊥BC于H,交DG于P,已知BC=48,AH=16,那么S正方形DGEF=.
12. 如图:正方形DGFE的边EF在△ABC边BC上,顶点D、G分别在边AB、AC上,AH⊥BC于H,交DG于P,已知BC=48,AH=16,那么S正方形DGEF=.
三、作图题
-
13. 如图,在7×4方格纸中,点A,B,C都在格点上,用无刻度直尺作图.
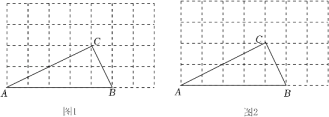 (1)、在图1中的线段AC上找一个点E,使AE=AC;(2)、在图2中作一个格点△CDE,使△CDE与△ABC相似.
(1)、在图1中的线段AC上找一个点E,使AE=AC;(2)、在图2中作一个格点△CDE,使△CDE与△ABC相似.四、解答题
-
14. 如图

【感知】如图①在△ABC中,点D为边BA延长线上的点,若= , 过点D作DE∥BC交CA延长线于点E.若DE=5,求BC的长.
【探究】如图②,在△ABC中,点D是边AB上的点,点E为边AC的中点,连接BE、CD交于点F,若=.小明尝试探究的值,在图②中.小明过点D作DM∥AC交BE于点M,易证△DFM∽△CFE,则==.从而得到的值为 ▲ , 易证△DBM∽△ABE,则= , 从而得到的值为 ▲ , 从而得到的值为 ▲ .
【应用】如图③,在△ABC中,点D是边AB上的点,E为边CA延长线上的点,连接BE,延长CD,交BE于点F.= , = , 且△ACD的面积为1,则△BDF的面积为 ▲ .
五、综合题
-
15. 综合与探究
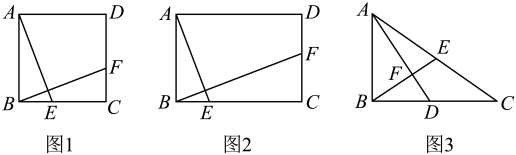 (1)、如图1,在正方形中,点分别在边上,且 , 请直接写出线段与的数量关系 .(2)、【类比探究】
(1)、如图1,在正方形中,点分别在边上,且 , 请直接写出线段与的数量关系 .(2)、【类比探究】如图2,在矩形中, , , 点分别在边上,且 , 请写出线段与的数量关系,并证明你的结论.
(3)、【拓展延伸】如图3,在中, , D为中点,连接 , 过点B作于点F,交于点E,若 , , 求的长.
-
-