云南省部分名校2023届高三上学期数学11月联考试卷

试卷更新日期：2022-12-28 类型：期中考试

进入出卷网下载

一、单选题

1. 命题“ $\forall x \in R ， l n (x^{2} + 1) > 0$ ”的否定为（）

A、 $\forall x \notin R ， l n (x^{2} + 1) \leq 0$ B、 $\exists x \in R ， l n (x^{2} + 1) \leq 0$ C、 $\forall x \in R ， l n (x^{2} + 1) \leq 0$ D、 $\exists x \notin R ， l n (x^{2} + 1) \leq 0$

查看试题解析
2. 已知复数 $z$ 在复平面内对应的点为 $(1 ， - 2)$ ，则 $z - 2 \bar{z} =$ （）

A、 $- 1 - 6 i$ B、 $- 1 + 6 i$ C、 $1 - 6 i$ D、 $1 + 6 i$

查看试题解析
3. 已知集合 $M = {x ∣ 4 x^{2} - 7 x - 2 < 0}$ ， $N = {x ∣ x + 1 \geq \frac{3}{2}}$ ，则 $M \cap N =$ （）

A、 ${x ∣ - \frac{1}{4} < x < 2}$ B、 ${x ∣ - \frac{1}{2} < x < 2}$ C、 ${x ∣ \frac{1}{2} \leq x < 2}$ D、 ${x ∣ - \frac{1}{2} \leq x < 2}$

查看试题解析
4. 随着社会的发展，人与人的交流变得便捷，信息的获取、传输和处理变得频繁，这对信息技术的要求越来越高，无线电波的技术也越来越成熟.已知电磁波在空间中自由传播时能损耗公式为 $L = 32.4 + 20 (l g D + l g F)$ ，其中D为传输距离 $($ 单位： $k m)$ ， F为载波频率 $($ 单位： $M H z)$ ， L为传输损耗 $($ 单位： $d B) .$ 若载波频率变为原来的100倍，传输损耗增加了60 dB，则传输距离变为原来的（）

A、100倍 B、50倍 C、10倍 D、5倍

查看试题解析
5. 已知函数 $f (x) = c o s x$ ， $g (x) = \frac{6 x}{x^{2} + 1}$ ，若函数 $h (x)$ 在 $[- \frac{π}{2} ， \frac{π}{2}]$ 上的大致图象如图所示，则 $h (x)$ 的解析式可能是（）

A、 $h (x) = f (x) + g (x)$ B、 $h (x) = f (x) - g (x)$ C、 $h (x) = \frac{f (x)}{g (x)}$ D、 $h (x) = f (x) g (x)$

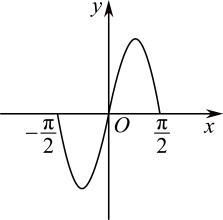查看试题解析
6. 某正方体的平面展开图如图所示，在这个正方体中，下列结论正确的是（）

A、 $A F / /$ 平面 $B C E$ B、 $A D ⊥$ 平面 $B C E$ C、 $A E / / B C$ D、 $B F ⊥ C E$

查看试题解析
7. 已知正数 $a ， b$ 满足 $(a + 5 b) (2 a + b) = 36$ ，则 $a + 2 b$ 的最小值为（）

A、16 B、12 C、8 D、4

查看试题解析
8. 某大学为了制作“迎新杯”篮球赛创意冠军奖杯，在全校学生中开展“迎新杯”篮球赛奖杯的创意设计征集活动.同学甲设计的创意奖杯如图1所示，从其轴截面中抽象出来的平面图形如图2所示，若圆O的半径为10cm， $A B = B C = C D$ ， $B C / / A D$ ， $∠ A B C = ∠ B C D = 120 ° .$ 甲在奖杯的设计与制作的过程中发现，当OB越长时，该奖杯越美观，则当该奖杯最美观时， $A D =$ （）

A、10cm B、 $10 \sqrt{2} c m$ C、 $10 \sqrt{3} c m$ D、 $5 \sqrt{6} c m$

查看试题解析

二、多选题

9. 已知函数 $f (x) = x^{3} + \frac{1}{2} x^{2} - 4 x$ ，则（）

A、 $x = 1$ 是 $f (x)$ 的极小值点 B、 $f (x)$ 有两个极值点 C、 $f (x)$ 的极小值为 $1$ D、 $f (x)$ 在 $[0 ， 2]$ 上的最大值为 $2$

查看试题解析
10. 函数 $f (x) = s i n (2 x - \frac{π}{3})$ 的图象向左平移 $\frac{π}{4}$ 个单位长度，得到函数 $g (x)$ 的图象，则下列结论正确的有（）

A、直线 $x = - \frac{5 π}{6}$ 是 $g (x)$ 图象的一条对称轴 B、 $g (x)$ 在 $(- \frac{π}{2} ， \frac{π}{6})$ 上单调递增 C、若 $g (x)$ 在 $(0 ， α)$ 上恰有4个零点，则 $α \in (\frac{23 π}{12} ， \frac{29 π}{12}]$ D、 $g (x)$ 在 $[\frac{π}{4} ， \frac{π}{2}]$ 上的最大值为 $\frac{1}{2}$

查看试题解析
11. 已知正三棱锥 $S - A B C$ 的底面边长为6，体积为 $6 \sqrt{3}$ ， A，B，C三点均在以S为球心的球S的球面上，P是该球面上任意一点，下列结论正确的有（）

A、三棱锥 $P - A B C$ 体积的最大值为 $18 \sqrt{3}$ B、三棱锥 $P - A B C$ 体积的最大值为 $27 \sqrt{3}$ C、若 $P A ⊥$ 平面ABC，则三棱锥 $P - A B C$ 的表面积为 $24 + 9 \sqrt{3} + 3 \sqrt{43}$ D、若 $P A ⊥$ 平面ABC，则异面直线AB与PC所成角的余弦值为 $\frac{3 \sqrt{13}}{26}$

查看试题解析
12. 已知等差数列 ${a_{n}}$ 的前n项和为 $S_{n}$ ，且 $S_{11} < S_{7} .$ 若存在实数a，b，使得 $a + b = 3$ ，且 $e^{a - 2 b} - 1 ⩽ S_{17} ⩽ l n (a - 2 b + 1)$ ，当 $n = k$ 时， $S_{n}$ 取得最大值，则 $k + 2 a - b$ 的值可能为（）

A、13 B、12 C、11 D、10

查看试题解析

三、填空题

13. 若函数 $f (x) = {\begin{array}{l} {(\frac{1}{2})}^{x} - 4 ， x \leq 0 \\ x^{2} - x + 1 ， x > 0 \end{array}$ 则 $f (f (- 3)) =$ .

查看试题解析
14. 已知 $t a n α = 4$ ， $β$ 满足① $s i n β > 0$ ，且 $s i n β = 1 + c o s β$ ， ② $t a n (2 α + β) = - \frac{10}{23}$ 两个条件中的一个，则 $t a n (α + β)$ 的一个值可以为.

查看试题解析
15. 已知数列 ${a_{n}}$ 满足 $a_{1} = - 3$ ， $a_{n} a_{n + 1} = a_{n} - 1$ ，则 $a_{105} =$ .

查看试题解析
16. 最早对勾股定理进行证明的是三国时期吴国的数学家赵爽，赵爽创制了一幅“勾股圆方图”，他用数形结合的方法，给出了勾股定理的详细证明.如图，某数学探究小组仿照“勾股圆方图”，利用6个全等的三角形和一个小的正六边形ABCDEF，拼成一个大的正六边形GHMNPQ，若 $A B = A G = 1$ ，则 $\vec{B E} \cdot \vec{G D} =$ .

查看试题解析

四、解答题

17. 已知 $f (x) = \frac{a x^{3} + (a + 1) x^{2} + 2 a + 4}{x}$ 是奇函数.

(1)、求a的值；

(2)、求 $f (x)$ 的值域.

查看试题解析
18. 在 $△ A B C$ 中，内角 $A ， B ， C$ 的对边分别为 $a ， b ， c$ ，已知 $\sqrt{3} b s i n (B + C) + a c o s B = c$ .

(1)、求角A的大小；

(2)、若 $a = 6 ， b + c = 6 + 6 \sqrt{3}$ ，求 $△ A B C$ 的面积.

查看试题解析
19. 如图，在四棱锥 $P - A B C D$ 中，底面 $A B C D$ 是正方形， $△ P A D$ 是等边三角形，平面 $P A D ⊥$ 平面 $A B C D$ ， $E ， F$ 分别是 $P C ， A B$ 的中点.

(1)、证明： $P C ⊥$ 平面 $D E F .$

(2)、求二面角 $B - D E - F$ 的余弦值.

查看试题解析
20. 已知函数 $f (x) = \frac{x^{m}}{m^{x}} - 1 .$

(1)、若 $m = 2$ ，求 $f (x)$ 的图象在 $x = 1$ 处的切线方程；

(2)、若 $0 < m < 1$ ，证明： $f (x)$ 在 $(0 ， + \infty)$ 上只有一个零点.

查看试题解析
21. 在数列 ${a_{n}}$ 中， $a_{1} = 1$ ，且 $a_{n + 1} = \frac{a_{n}}{2 a_{n} + 2}$ .

(1)、证明数列 ${\frac{1}{a_{n}} + 2}$ 是等比数列，并求 ${a_{n}}$ 的通项公式；

(2)、若 $b_{n} = \frac{n}{a_{n}}$ ，求数列 ${b_{n}}$ 的前 $n$ 项和 $S_{n}$ .

查看试题解析
22. 已知函数 $f (x) = x l n x - (2 a + 1) x$ .

(1)、求 $f (x)$ 的单调区间；

(2)、证明： $f (x) + (2 a + 1) x > s i n x - 1$ .

查看试题解析