陕西省宝鸡市陈仓区2022-2023学年高一上学期数学期中试卷
试卷更新日期:2022-12-28 类型:期中考试
一、单选题
-
1. 下列所给对象能构成集合的是( )A、2020年全国I卷数学试题的所有难题 B、比较接近2的全体正数 C、未来世界的高科技产品 D、所有整数2. 命题“”的否定是( )A、 B、 C、 D、3. 下列四个图象中,是函数图象的是( )
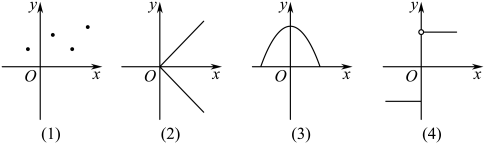 A、(1) B、(3)(4) C、(1)(2)(3) D、(1)(3)(4)4. 已知 是一次函数,且 ,则 的解析式为( )A、 B、 C、 D、5. 已知函数的图象关于对称,且在上单调递增,设 , , , 则、、的大小关系为( )A、 B、 C、 D、6. 集合 , , 则( )A、 B、 C、 D、7. “关于x的不等式对恒成立”的一个必要不充分条件是( )A、 B、 C、 D、8. 已知函数 是定义在R上的增函数,则a的取值范围是( )A、 B、 C、 D、
A、(1) B、(3)(4) C、(1)(2)(3) D、(1)(3)(4)4. 已知 是一次函数,且 ,则 的解析式为( )A、 B、 C、 D、5. 已知函数的图象关于对称,且在上单调递增,设 , , , 则、、的大小关系为( )A、 B、 C、 D、6. 集合 , , 则( )A、 B、 C、 D、7. “关于x的不等式对恒成立”的一个必要不充分条件是( )A、 B、 C、 D、8. 已知函数 是定义在R上的增函数,则a的取值范围是( )A、 B、 C、 D、二、多选题
-
9. 方程组的解集以下表示正确的为( )A、 B、 C、 D、10. 对于实数a,b,c,下列命题是真命题的为( )A、若a>b,则ac<bc B、若 , 则a>b C、若a<b<0,则a2>ab>b2 D、若a>0>b,则|a|<|b|11. 已知函数是偶函数,且其定义域为 , 则( )A、 B、 C、函数的定义域为 D、函数的最大值为12. 已知函数f(x)=xa的图象经过点( , 2),则( )A、f(x)的图象经过点(2,4) B、f(x)的图象关于原点对称 C、f(x)在(0,+∞)上单调递增 D、f(x)在(0,+∞)内的值域为(0,+∞)
三、填空题
-
13. 函数f(x)= (x≥2)的最大值为 .14. 已知集合 , 则 .15. 比较下面两个数的大小16. 规定记号“⊕”表示一种运算,即(a,b为正实数),若正数x,y满足 , 则xy的最小值是.
四、解答题
-
17. 证明函数在上是增函数.18. 已知集合 , , .(1)、求 , ;(2)、求.19. 关于的不等式的解集为或 ,(1)、求关于的不等式的解集(2)、求关于的不等式的解集.