辽宁省葫芦岛市四校2022-2023学年高三上学期数学期中考试试卷

试卷更新日期：2022-12-28 类型：期中考试

进入出卷网下载

一、单选题

1. 已知集合 $A = {x | y = \frac{1}{\sqrt{1 - 2^{x}}}}$ ， $B = {y | y = - | x - 3 | - 2}$ ，则 $A ∪ B =$ （）

A、 $\emptyset$ B、 $(- \infty ， - 2]$ C、 $(- \infty ， 0)$ D、 $(- \infty ， 0]$

查看试题解析
2. 若复数 $z$ 满足 $(z - 1) (1 + i) = 2 - 2 i$ ，则 $| z | =$ （）

A、 $\sqrt{5}$ B、 $\sqrt{3}$ C、5 D、 $\sqrt{2}$

查看试题解析
3. 函数 $y = a^{3 - x}$ （ $a > 0$ ，且 $a \neq 1$ ）的图象恒过定点 $A$ ，若点 $A$ 在椭圆 $\frac{x^{2}}{m} + \frac{y^{2}}{n} = 1$ （ $m > 0$ ， $n > 0$ ）上，则 $m + n$ 的最小值为（）

A、12 B、14 C、16 D、18

查看试题解析
4. 函数 $f (x) = \frac{3 \sin x}{2^{| x |}} + x \cos x$ 在 $[- 2 π ， 2 π]$ 的图象大致为（）

A、 B、 C、 D、

查看试题解析
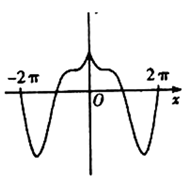5. 从混有 $5$ 张假钞的 $20$ 张百元钞票中任意抽出 $2$ 张，将其中 $1$ 张放到验钞机上检验发现是假钞，则另 $1$ 张也是假钞的概率为（）

A、 $\frac{1}{19}$ B、 $\frac{4}{19}$ C、 $\frac{2}{17}$ D、 $\frac{17}{38}$

查看试题解析
6. 在等腰梯形 $A B C D$ 中， $A B / / D C ， A B = 2 B C = 2 C D = 2 ， P$ 是腰 $A D$ 上的动点，则 $| 2 \vec{P B} - \vec{P C} |$ 的最小值为（）

A、 $\sqrt{7}$ B、3 C、 $\frac{3 \sqrt{3}}{2}$ D、 $\frac{27}{4}$

查看试题解析
7. 已知变量x，y的关系可以用模型 $y = c \cdot e^{k x}$ 拟合，设 $z = l n y$ ，其变换后得到一组数据下：
$x$
16
17
18
19
$z$
50
34
41
31
由上表可得线性回归方程 $z = - 4 x + a$ ，则c＝（　　）

A、 $- 4$ B、 $e^{- 4}$ C、109 D、 $e^{109}$

查看试题解析
8. 已知双曲线 $\frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1 (a > 0 ， b > 0)$ 左右焦点为 $F_{1}$ ， $F_{2}$ ，过 $F_{2}$ 的直线与双曲线的右支交于 $P$ ， $Q$ 两点，且 ${\vec{P F}}_{2} = 3 \vec{F_{2} Q}$ ，若 $△ P Q F_{1}$ 为以 $Q$ 为顶角的等腰三角形，则双曲线的离心率为（）

A、3 B、2 C、 $\sqrt{2}$ D、 $\sqrt{3}$

查看试题解析

二、多选题

9. 若函数 $f (x) = c o s (ω x + \frac{π}{3})$ 两条对称轴之间的最小距离为 $\frac{π}{2}$ ，则下列说法正确的是（）

A、函数 $f (x)$ 的最小正周期为 $π$ B、函数 $f (x)$ 在 $[0 ， \frac{π}{2}]$ 上单调递减 C、将函数 $f (x)$ 图象向右平移 $\frac{π}{6}$ 个单位长度后所得图象关于 $y$ 轴对称 D、若 $f (x_{1}) = f (x_{2}) = 0$ ，则 $f (x_{1} + x_{2}) = \frac{\sqrt{3}}{2}$

查看试题解析
10. 已知 $a > 0$ ， $b > 0$ ， $a \log_{4} 2 + b \log_{16} \sqrt{2} = \frac{5}{16}$ ，则下列结论正确的是（）

A、 $4 a + b = 5$ B、 $4 a + b = \frac{5}{2}$ C、ab的最大值为 $\frac{25}{64}$ D、 $\frac{1}{a} + \frac{1}{b}$ 的最小值为 $\frac{18}{5}$

查看试题解析
11. 已知点 $A (- 1 ， 0) ， B (1 ， 0)$ ，若圆 ${(x - 2 a + 1)}^{2} + {(y - 2 a - 2)}^{2} = 1$ 上存在点M满足 $\vec{M A} \cdot \vec{M B} = 3$ ，则实数 $a$ 的值为（）

A、 $- 2$ B、 $- 1$ C、2 D、0

查看试题解析
12. 香囊，又名香袋､花囊，是我国古代常见的一种民间刺绣工艺品，香囊形状多样，如图1所示的六面体就是其中一种，已知该六面体的所有棱长均为2，其平面展开图如图2所示，则下列说法正确的是（）

A、AB⊥DE B、直线CD与直线EF所成的角为45° C、该六面体的体积为 $\frac{2 \sqrt{2}}{3}$ D、该六面体内切球的表面积是 $\frac{32 π}{27}$

查看试题解析

三、填空题

13. ${(1 - 2 x)}^{5} {(1 + 3 x)}^{4}$ 的展开式中按 $x$ 的升幂排列的第3项的系数为.

查看试题解析
14. 已知向量 $\vec{a}$ ， $\vec{b}$ 的夹角为60°，且 $| \vec{a} | = 2$ ， $| \vec{b} | = 1$ ，则 $| \vec{a} - 2 \vec{b} | =$ .

查看试题解析
15. 若两曲线 $y = x^{2} - 1$ 与 $y = a \ln x - 1$ 存在公切线，则正实数 $a$ 的取值范围是．

查看试题解析
16. 已知数列 ${a_{n}}$ 满足 $a_{n} = l o g_{2} (\frac{n + 2}{n + 1})$ ．给出定义：使数列 ${a_{n}}$ 的前 $k$ 项和为正整数的 $k$ $(k \in N^{*})$ 叫做“好数”，则在 $[1 ， 2021]$ 内的所有“好数”的和为．

查看试题解析

四、解答题

17. 已知函数 $f (x) = M \sin (ω x + φ) (M > 0 ， | φ | < \frac{π}{2})$ 的部分图象如图所示.

(1)、求函数 $f (x)$ 的解析式；

(2)、在 $△ A B C$ 中，角A，B，C的对边分别是 a，b，c，若 $(2 a - c) \cos B = b \cos C$ ，求 $f (\frac{A}{2})$ 的取值范围.

查看试题解析
18. 在数列 ${a_{n}}$ 中， $a_{1} = 1 ， a_{n + 1} = \frac{a_{n}}{c a_{n} + 1} (c > 0)$ ，且 $a_{1} ， a_{2} ， a_{5}$ 成等比数列．

(1)、证明数列 ${\frac{1}{a_{n}}}$ 是等差数列，并求 ${a_{n}}$ 的通项公式；

(2)、设数列 ${b_{n}}$ 满足 $b_{n} = (4 n^{2} + 1) a_{n} a_{n + 1}$ ，其前 $n$ 项和为 $S_{n}$ ，证明： $S_{n} < n + 1$ ．

查看试题解析
19. 如图，在四棱锥 $P - A B C D$ 中，平面 $P A B ⊥$ 平面 $A B C D$ ， $B C // A D$ ， $∠ B A D = 90 °$ ， $P A = A D = 2 A B = 4 B C = 4$ ， $P C = \sqrt{21}$

(1)、证明： $P A ⊥$ 平面 $A B C D$ ；

(2)、线段 $A B$ 上是否存在一点 $M$ ，使得 $M C$ 与平面 $P C D$ 所成角的正弦值为 $\frac{\sqrt{221}}{17}$ ?若存在，请求出 $\frac{A M}{A B}$ 的值；若不存在，请说明理由.

查看试题解析
20. 2020年春天随着疫情的有效控制，高三学生开始返校复课学习.为了减少学生就餐时的聚集排队时间，学校食堂从复课之日起，每天中午都会提供 $A$ 、 $B$ 两种套餐（每人每次只能选择其中一种），经过统计分析发现：学生第一天选择 $A$ 类套餐的概率为 $\frac{2}{3}$ 、选择 $B$ 类套餐的概率为 $\frac{1}{3}$ ．而前一天选择了 $A$ 类套餐第二天选择 $A$ 类套餐的概率为 $\frac{1}{4}$ 、选择 $B$ 套餐的概率为 $\frac{3}{4}$ ；前一天选择 $B$ 类套餐第二天选择 $A$ 类套餐的概率为 $\frac{1}{2}$ 、选择 $B$ 类套餐的概率也是 $\frac{1}{2}$ ，如此往复．记某同学第 $n$ 天选择 $A$ 类套餐的概率为 $P_{n}$ ．

(1)、证明数列 ${P_{n} - \frac{2}{5}}$ 是等比数列，并求数列 ${P_{n}}$ 的通项公式；

(2)、记高三某宿舍的3名同学在复课第二天选择 $A$ 类套餐的人数为 $X$ ，求 $X$ 的分布列并求 $E (X)$ ；

(3)、为了贯彻五育并举的教育方针，培养学生的劳动意识，一个月后学校组织学生利用课余时间参加志愿者服务活动，其中有20位学生负责为全体同学分发套餐．如果你是组长，如何安排分发 $A$ 、 $B$ 套餐的同学的人数呢，说明理由．

查看试题解析
21. 已知 $P (\frac{2}{3} ， \frac{2 \sqrt{6}}{3})$ 是椭圆C： $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 与抛物线E： $y^{2} = 2 p x (p > 0)$ 的一个公共点，且椭圆与抛物线具有一个相同的焦点 $F$ .

(1)、求椭圆C及抛物线 $E$ 的方程；

(2)、A，B是椭圆C上的两个不同点，若直线 $O A$ ， $O B$ 的斜率之积为 $- \frac{3}{4}$ （注： $O$ 为坐标原点），点 $M$ 是线段 $O A$ 的中点，连接 $B M$ 并延长交椭圆 $C$ 于点 $N$ ，求 $\frac{| B M |}{| M N |}$ 的值.

查看试题解析
22. 已知函数 $f (x) = l n x + \frac{a - e}{x}$ ，其中e是自然对数的底数．

(1)、设直线 $y = \frac{2}{e} x - 2$ 是曲线 $y = f (x) (x > 1)$ 的一条切线，求 $a$ 的值；

(2)、若 $\exists a \in R$ ，使得 $f (x) + m a \geq 0$ 对 $\forall x \in (0 ， + \infty)$ 恒成立，求实数 $m$ 的取值范围．

查看试题解析

$x$	16	17	18	19
$z$	50	34	41	31