广西柳州市2022-2023学年高一上学期数学12月联考试卷

试卷更新日期：2022-12-27 类型：月考试卷

进入出卷网下载

一、单选题

1. 设集合 $A = {1 ， 2 ， 3 ， 4 ， 5}$ ， $B = {x | x^{2} - 5 x + 4 < 0}$ ，则 $A ∩ B =$ （）

A、 ${1}$ B、 ${1 ， 2}$ C、 ${2 ， 3}$ D、 $\emptyset$

查看试题解析
2. 下列函数中，与 $y = x$ 是同一个函数的是（）

A、 $y = {(\sqrt{x})}^{2}$ B、 $u = \sqrt[3]{v^{3}}$ C、 $y = \sqrt{x^{2}}$ D、 $m = \frac{n^{2}}{n}$

查看试题解析
3. 已知 $c o s α = - \frac{5}{13}$ ，且 $α$ 为第二象限角，则 $t a n α =$ （）

A、 $- \frac{12}{5}$ B、 $- \frac{5}{12}$ C、 $- \frac{12}{13}$ D、 $- \frac{13}{12}$

查看试题解析
4. 已知 $a$ 、 $b$ 、 $c \in R$ ，且 $a > b$ ，则下列不等式成立的是（）

A、 $a^{2} > b^{2}$ B、 $| a | > | b |$ C、 $a + c > b + c$ D、 $a c > b c$

查看试题解析
5. 已知 $f (x + 1) = x^{2} + 2 x (x \in R)$ ，则函数 $f (x)$ 的解析式是（）

A、 $f (x) = x^{2} + 1 (x \in R)$ B、 $f (x) = x^{2} - 1 (x \in R)$ C、 $f (x) = x^{2} - 1 (x \geq 1)$ D、 $f (x) = x^{2} + 1 (x \geq 1)$

查看试题解析
6. 如图， $△ A B C$ 是边长为2的等边三角形，点 $E$ 由点 $A$ 沿线段 $A B$ 向点 $B$ 移动，过点 $E$ 作 $A B$ 的垂线 $l$ ，设 $A E = x$ ，记位于直线 $l$ 左侧的图形的面积为 $y$ ，那么 $y$ 与 $x$ 的函数关系的图象大致是（）

A、 B、 C、 D、

查看试题解析
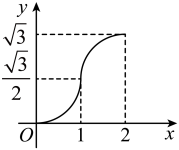7. 按照国家标准，教室内空气中二氧化碳日平均最高容许浓度应小于等于0.1%经测定，刚下课时，空气中含有0.2%的二氧化碳，若开窗通风后教室内二氧化碳的浓度为 $y %$ ，且 $y$ 随时间 $t$ （单位：分钟）的变化规律可以用函数 $y = 0.05 + λ e^{- \frac{t}{10}} (λ \in R)$ 描述，则该教室内的二氧化碳浓度达到国家标准至少需要的时间为（）（参考数据 $l n 3 \approx 1.1$ ）

A、8.8分钟 B、11分钟 C、13.2分钟 D、22分钟

查看试题解析
8. 已知 $f (x)$ 是奇函数，在区间 $(- ∞ ， 0)$ 上是增函数，又 $f (- 3) = 0$ ，那么 $x f (x) < 0$ 的解集是（）

A、 ${x | - 3 < x < 0$ 或 $x > 3}$ B、 ${x | x < - 3$ 或 $x > 3}$ C、 ${x | x < - 3$ 或 $0 < x < 3}$ D、 ${x | - 3 < x < 0$ 或 $0 < x < 3}$

查看试题解析

二、多选题

9. 与 $- 835 °$ 终边相同的角有（）

A、 $- 245 °$ B、 $245 °$ C、 $- 115 °$ D、 $- 475 °$

查看试题解析
10. 下列大小关系中正确的是（）

A、 $9^{1.5} > 3^{2.7}$ B、 ${(\frac{3}{7})}^{\frac{4}{7}} < {(\frac{4}{7})}^{\frac{3}{7}}$ C、 $l o g_{\frac{1}{2}} \frac{1}{3} < l o g_{3} \frac{1}{2}$ D、 $1 . 7^{0.2} > 0 . 9^{2.1}$

查看试题解析
11. 中国传统文化中很多内容体现了数学的“对称美”，如图所示的太极图是由黑白两个鱼形纹组成的圆形图案，充分体现了相互转化、对称统一的形式美、和谐美．定义：图象能够将圆 $O$ 的周长和面积同时等分成两部分的函数称为圆 $O$ 的一个“太极函数”，则下列结论正确的是（）

A、对于任意一个圆 $O$ ，其“太极函数”有无数个 B、函数 $f (x) = x^{3}$ 可以同时是无数个圆的“太极函数” C、函数 $f (x) = \frac{1}{x}$ 可以是某个圆的“太极函数” D、函数 $y = f (x)$ 是“太极函数”的充要条件为函数 $y = f (x)$ 的图象是中心对称图形

查看试题解析
12. 已知函数 $f (x) = {\begin{array}{l} | x - 1 | ， x \leq 2 \\ l o g_{\frac{1}{2}} (x - \frac{3}{2}) ， x > 2 \end{array}$ ，若 $f (x + a) \geq f (x)$ 恒成立．则实数 $a$ 的取值可以是（）

A、2 B、 $- 3$ C、 $- \frac{9}{4}$ D、 $- 1$

查看试题解析

三、填空题

13. 函数 $f (x) = \sqrt{1 - x} + \sqrt{x + 2} + 1$ 的定义域为．

查看试题解析
14. 已知函数 $f (x) = {\begin{array}{l} e^{x} ， x ≤ 0 \\ l n x ， x > 0 \end{array}$ ，则 $f (\frac{1}{e}) =$ .

查看试题解析
15. 若一元二次不等式 $4 k x^{2} + 2 k x - \frac{3}{4} < 0$ 对一切实数 $x$ 都成立，则实数 $k$ 的取值范围为．

查看试题解析
16. 若函数 $f (x) = - 2 x + 3$ 经过点 $(a ， b)$ ， $a > 0$ 且 $b > 0$ ，则 $\frac{1}{a + 1} + \frac{2}{b}$ 的最小值为．

查看试题解析

四、解答题

17. 已知集合 $P = {x | a + 1 \leq x \leq 2 a + 1}$ ，集合 $Q = {x | - 2 \leq x \leq 5}$

(1)、若 $a = 3$ ，求集合 $(C_{R} P) ∩ Q$ ；

(2)、若 $P \subseteq Q$ ，求实数 $a$ 的取值范围.

查看试题解析
18. 已知 $\frac{1 + 2 s i n α c o s α}{c o s^{2} α - s i n^{2} α} = 2$ ．

(1)、求 $t a n α$ 的值；

(2)、求 $2 s i n^{2} α + 3 s i n α c o s α - c o s^{2} α$ 的值．

查看试题解析
19. 化简求值（需要写出计算过程）

(1)、若 $10 0^{a} = 4$ ， $1 0^{b} = 25$ ，求 $2 a + b$ 的值；

(2)、 ${(\frac{8}{27})}^{- \frac{2}{3}} + e^{l n 2} + l o g_{\frac{1}{4}} \sqrt{2} - l o g_{3} 32 \cdot l o g_{2} 3$ ．

查看试题解析
20. 某公司为了提高生产效率，决定投入160万元买一套生产设备，预计使用该设备后，前 $n (n \in N^{*})$ 年的支出成本为 $(10 n^{2} - 2 n)$ 万元，每年的销售收入98万元．

(1)、估计该设备从第几年开始实现总盈利；

(2)、使用若干年后对该设备处理的方案有两种：
方案一：当总盈利额达到最大值时，该设备以20万元的价格处理；
方案二：当年平均盈利额达到最大值时，该设备以30万元的价格处理．
哪种方案较为合理？并说明理由．（注：年平均盈利额 $= \frac{总盈利额}{年度}$ ）

查看试题解析
21. 已知 $f (x)$ 定义域为 $R$ ，对任意 $x ， y \in R$ 都有 $f (x + y) = f (x) + f (y) - 1$ ，当 $x > 0$ 时， $f (x) > 1$ ， $f (- 1) = 2$ ．

(1)、试判断 $f (x)$ 在 $R$ 上的单调性，并证明；

(2)、解不等式： $f (3 x^{2} - 4 x - 2) + 2 f (x) > 4$ ．

查看试题解析
22. 已知函数 $f (x) = \frac{b \cdot 2^{x} - c}{2^{x} + b}$ ， $g (x) = l o g_{a} \frac{x - 1}{x + b}$ （ $a > 0$ 且 $a \neq 1$ ）， $g (x)$ 的定义域关于原点对称， $f (0) = 0$ ．

(1)、求 $b$ 的值，判断函数 $g (x)$ 的奇偶性并说明理由；

(2)、求函数 $f (x)$ 的值域；

(3)、若关于 $x$ 的方程 $m [f (x)]^{2} - (m - 1) f (x) - 2 = 0$ 有解，求实数 $m$ 的取值范围．

查看试题解析