安徽省六安市霍邱县2022-2023学年八年级上学期第三次月考数学试卷
试卷更新日期:2022-12-27 类型:月考试卷
一、单选题
-
1. 下列各选项中的两个图形属于全等形的是( )A、
 B、
B、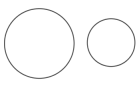 C、
C、 D、
D、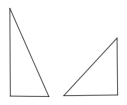 2. 将点先向右平移5个单位长度,再向下平移6个单位长度得到的点的坐标是( )A、 B、 C、 D、3. 如图, , 是的高线,与相交于点 . 若 , 则能判断的依据是( )
2. 将点先向右平移5个单位长度,再向下平移6个单位长度得到的点的坐标是( )A、 B、 C、 D、3. 如图, , 是的高线,与相交于点 . 若 , 则能判断的依据是( ) A、 B、 C、 D、4. 在中, , , , 则的取值范围是( )A、 B、 C、 D、5. 如图,点 , , , 在一条直线上, , , 添加下列条件仍不能判断的是( )
A、 B、 C、 D、4. 在中, , , , 则的取值范围是( )A、 B、 C、 D、5. 如图,点 , , , 在一条直线上, , , 添加下列条件仍不能判断的是( ) A、 B、 C、 D、6. 如图,已知 , , , 则的度数为( )
A、 B、 C、 D、6. 如图,已知 , , , 则的度数为( ) A、 B、 C、 D、7. 如图,直线y1=k1x+b和直线y2=k2x+b分别与x轴交于A(-1,0)和B(3,0)两点,则不等式组 的解集为( )
A、 B、 C、 D、7. 如图,直线y1=k1x+b和直线y2=k2x+b分别与x轴交于A(-1,0)和B(3,0)两点,则不等式组 的解集为( ) A、 B、 C、 D、 或8. 如图,在的正方形方格中,每个小正方形方格的边长都为1,则和的关系是( )
A、 B、 C、 D、 或8. 如图,在的正方形方格中,每个小正方形方格的边长都为1,则和的关系是( ) A、 B、 C、 D、9. 如图所示 , , , 点 , , 在一条直线上,若 , , 则的长为( )
A、 B、 C、 D、9. 如图所示 , , , 点 , , 在一条直线上,若 , , 则的长为( )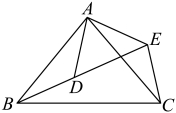 A、2 B、5 C、8 D、1510. 如图,在中, , 是高,是角平分线,交于点 , 过点作 , 垂足为 , 下面说法中不一定正确的是( )
A、2 B、5 C、8 D、1510. 如图,在中, , 是高,是角平分线,交于点 , 过点作 , 垂足为 , 下面说法中不一定正确的是( ) A、 B、 C、 D、的周长等于线段的长
A、 B、 C、 D、的周长等于线段的长二、填空题
-
11. 若点到轴的距离为4,则n= .12. 定理“直角三角形的两个锐角互余”的逆定理是 .13. 已知一次函数 , 若函数满足 , 则自变量的取值范围是 .14. 如图,是等腰三角形,点 , 分别在腰 , 上,且 , , 连接 , 交于点 . 则:
 (1)、图中有对全等三角形;(2)、若点恰好为的中点,且的面积为2,则四边形的面积为 .
(1)、图中有对全等三角形;(2)、若点恰好为的中点,且的面积为2,则四边形的面积为 .三、解答题
-
15. 已知点在平面直角坐标系内.(1)、若点在第四象限,求的取值范围;(2)、若点在坐标轴上,求的值.16. 如图,在中,延长至点 , 连接 , 是上一点.已知 , , , 求的度数.
 17. 已知直线与直线交于点 .(1)、求的坐标;(2)、若直线与轴交于点 , 直线与轴交于点 , 求的面积.18. 如图,△ABD≌△EBC,AB=3cm,BC=6cm,
17. 已知直线与直线交于点 .(1)、求的坐标;(2)、若直线与轴交于点 , 直线与轴交于点 , 求的面积.18. 如图,△ABD≌△EBC,AB=3cm,BC=6cm, (1)、求DE的长.(2)、若A、B、C在一条直线上,则DB与AC垂直吗?为什么?19. 课间,小明拿着老师的等腰直角三角板的三角板玩,不小心掉到两墙之间,如图所示.
(1)、求DE的长.(2)、若A、B、C在一条直线上,则DB与AC垂直吗?为什么?19. 课间,小明拿着老师的等腰直角三角板的三角板玩,不小心掉到两墙之间,如图所示. (1)、求证:;(2)、若 , 请你帮小明求出砌墙砖块的厚度的大小(每块砖的厚度相等).20. 求证:顶角是锐角的等腰三角形腰上的高与底边夹角等于其顶角的一半.
(1)、求证:;(2)、若 , 请你帮小明求出砌墙砖块的厚度的大小(每块砖的厚度相等).20. 求证:顶角是锐角的等腰三角形腰上的高与底边夹角等于其顶角的一半. (1)、根据题意补全下图,并根据题设和结论,结合图形,用符号语言补充写出“已知”和“求证”.
(1)、根据题意补全下图,并根据题设和结论,结合图形,用符号语言补充写出“已知”和“求证”.已知:在锐角中, , ▲ ;
求证: ▲ .
(2)、证明:21. 如图,在△ABC中,D为BC的中点,过D点的直线GF交AC于点F,交AC的平行线BG于点G,DE⊥GF,并交AB于点E,连接EG,EF.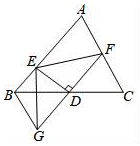 (1)、求证:BG=CF.(2)、请你猜想BE+CF与EF的大小关系,并说明理由.22. 为满足顾客的购物需求,某水果店计划购进甲、乙两种水果进行销售.经了解,购进2千克甲水果和3千克乙水果共需23元,购进3千克甲水果和1千克乙水果共需17元,已知甲,乙两种水果的售价分别为6元/千克和10元/千克.(1)、求甲、乙两种水果的进价分别是多少?(2)、若水果店购进这两种水果共200千克,其中甲种水果的重量不低于乙种水果重量的1.5倍,则水果店应如何进货才能获得最大利润,最大利润是多少?23. 我们规定:两组邻边分别相等的四边形叫做筝形四边形,如图1,四边形中,若 , , 则称四边形是筝形四边形.
(1)、求证:BG=CF.(2)、请你猜想BE+CF与EF的大小关系,并说明理由.22. 为满足顾客的购物需求,某水果店计划购进甲、乙两种水果进行销售.经了解,购进2千克甲水果和3千克乙水果共需23元,购进3千克甲水果和1千克乙水果共需17元,已知甲,乙两种水果的售价分别为6元/千克和10元/千克.(1)、求甲、乙两种水果的进价分别是多少?(2)、若水果店购进这两种水果共200千克,其中甲种水果的重量不低于乙种水果重量的1.5倍,则水果店应如何进货才能获得最大利润,最大利润是多少?23. 我们规定:两组邻边分别相等的四边形叫做筝形四边形,如图1,四边形中,若 , , 则称四边形是筝形四边形. (1)、如图2,筝形中, , , 对角线 , 相交于点 .
(1)、如图2,筝形中, , , 对角线 , 相交于点 .①求证:垂直平分;
②若 , 求证:;
(2)、如图3,筝形四边形中, , , 对角线 , 相交于点 , 若 , 求证: , 互相垂直平分.