安徽省淮北市五校联考2022-2023学年八年级上学期月考三数学试卷
试卷更新日期:2022-12-27 类型:月考试卷
一、单选题
-
1. 下列图形中,是轴对称图形的是( )A、
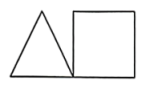 B、
B、 C、
C、 D、
D、 2. 计算的结果是( )A、 B、 C、 D、3. 如图,在中,点D在的延长线上,若 , , 则的度数为( )
2. 计算的结果是( )A、 B、 C、 D、3. 如图,在中,点D在的延长线上,若 , , 则的度数为( ) A、 B、 C、 D、4. 下列因式分解正确的是( )A、 B、 C、 D、5. 如图, , , , 则的度数是( )
A、 B、 C、 D、4. 下列因式分解正确的是( )A、 B、 C、 D、5. 如图, , , , 则的度数是( ) A、22° B、23° C、30° D、33°6. 在平面直角坐标系中,点与点关于轴对称,则的值为( )A、-3 B、-2 C、1 D、27. 已知: , , 则( )A、4 B、3 C、2 D、18. 在和中,下列条件不能判断这两个三角形全等的是( )A、 , , B、 , , C、 , , D、 , ,9. 如图,在中, , , 是边上的中线,则的长度可能为( )
A、22° B、23° C、30° D、33°6. 在平面直角坐标系中,点与点关于轴对称,则的值为( )A、-3 B、-2 C、1 D、27. 已知: , , 则( )A、4 B、3 C、2 D、18. 在和中,下列条件不能判断这两个三角形全等的是( )A、 , , B、 , , C、 , , D、 , ,9. 如图,在中, , , 是边上的中线,则的长度可能为( )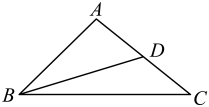 A、1 B、2 C、5 D、810. 如图,在中, , 平分 , 点E是的中点,点P是上一动点,连接 , 若 , , , 则的最小值是( )
A、1 B、2 C、5 D、810. 如图,在中, , 平分 , 点E是的中点,点P是上一动点,连接 , 若 , , , 则的最小值是( ) A、 B、6 C、 D、10
A、 B、6 C、 D、10二、填空题
-
11. 若有意义,则x的取值范围是 .12. 如图,是的边的垂直平分线,垂足为点E,交于点D,连接 , , , , 则的长为.
 13. 如图,在中,平分交于点D,平分交于点E,若 , 则 .
13. 如图,在中,平分交于点D,平分交于点E,若 , 则 .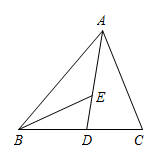 14. 如图,中, , 于点E,于点D,与相交于点F,且.
14. 如图,中, , 于点E,于点D,与相交于点F,且. (1)、计算.(2)、若 , , 则 .
(1)、计算.(2)、若 , , 则 .三、解答题
-
15. 计算:(1)、;(2)、 .16. 如图,在中,点D是的中点,过点D作交于点E,连接 . 若的周长为13, , 求的周长.
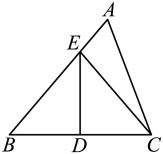 17. 已知中不含项和x项,求a,b的值.18. 如图,图中的小方格都是边长为1的正方形,在方格纸中的位置如图所示,已知点 , .
17. 已知中不含项和x项,求a,b的值.18. 如图,图中的小方格都是边长为1的正方形,在方格纸中的位置如图所示,已知点 , . (1)、请在方格纸中建立平面直角坐标系,画出轴,轴的位置,并写出点的坐标;(2)、请在图中作出关于y轴对称的图形;(3)、写出 , , 的坐标.19. 如图,在中,点D是延长线上一点,过点D作于点F,延长交于点E,交的平分线于点N,点M为与的交点, , .
(1)、请在方格纸中建立平面直角坐标系,画出轴,轴的位置,并写出点的坐标;(2)、请在图中作出关于y轴对称的图形;(3)、写出 , , 的坐标.19. 如图,在中,点D是延长线上一点,过点D作于点F,延长交于点E,交的平分线于点N,点M为与的交点, , . (1)、求的度数;(2)、证明:.20. 观察以下等式:
(1)、求的度数;(2)、证明:.20. 观察以下等式:第1个等式: ,
第2个等式: ,
第3个等式: ,
……
按照以上规律,解决下列问题:
(1)、写出第4个等式:;(2)、写出你猜想的第个等式(用含的式子表示),并验证当时,猜想成立.21. 如图,在中,延长至点D,使 , 过点D作 , 且 , 连接 .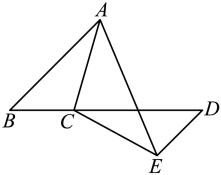 (1)、求证:;(2)、若 , , 求的度数.22. 如图,有足够多的边长为的小正方形(A类),宽为、长为的长方形(B类)以及边长为的大正方形(C类),发现利用图1中的三类图形可以拼出一些长方形来解释某些等式.
(1)、求证:;(2)、若 , , 求的度数.22. 如图,有足够多的边长为的小正方形(A类),宽为、长为的长方形(B类)以及边长为的大正方形(C类),发现利用图1中的三类图形可以拼出一些长方形来解释某些等式. (1)、尝试解决:
(1)、尝试解决:用图1中的若干个图形(三类图形都要用到)拼成一个正方形,使其面积为 , 画出图形,并根据图形回答 ▲ .
(2)、图2是由图1中的三类图形拼出的一个长方形,根据图2可以得到并解释等式:.(3)、用图1中的若干个图形(三类图形都要用到)拼成一个长方形,使其面积为 , 写出你的拼法,并根据你画的图形分解因式:.23. 在等腰中, , 点D在上,延长至点E,使 , 连接 . (1)、若 ,
(1)、若 ,①如图1,求证:;
②如图2,将绕点C按顺时针方向旋转一定的角度,使点A,D,E三点在一条直线上,判定的形状,并说明理由.
(2)、若 , 如图3,(1)中①的结论是否成立?若不成立,请给出 , 之间的数量关系;若成立,请给出证明.